Consider a cube of side $L_{1}$ at temperature $T_{1}^{\circ} C$ . Let it be heated to a temperature $T_{2}^{\circ} C$ when the length becomes $L_{2}$ show that $g \approx 3 a$ .

Text Solution

Verified by Experts

$Δ T = T_{2} - T_{1}$
We have $L_{2} = L_{1} (1 + a \times Δ T) and V_{2} = V_{1} (1 + y \times Δ T)$
But $V_{2} = L_{2}^{3} and V_{1} L_{1}^{3}$
$∴ \frac{V_{2}}{V_{1}} = {(\frac{L_{2}}{L_{1}})}^{3}$
$∴ 1 + y \times Δ T = {(1 + α \times Δ T)}^{3}$
$= 1 + {(a \times Δ T)}^{3} + 3 α \times Δ T + 3 {(α \times Δ T)}^{2}$
$∴ 1 + y \times Δ T \approx 1 + 3 α \times Δ T$
[Neglecting terms with $a^{2} and α^{3}]$
$∴ y \approx 3 α$ .

In following isothermal graphs A, B and C at temperatures $T_{1}, T_{2}$ and $T_{3}$ , the correct order of temperatures will be :

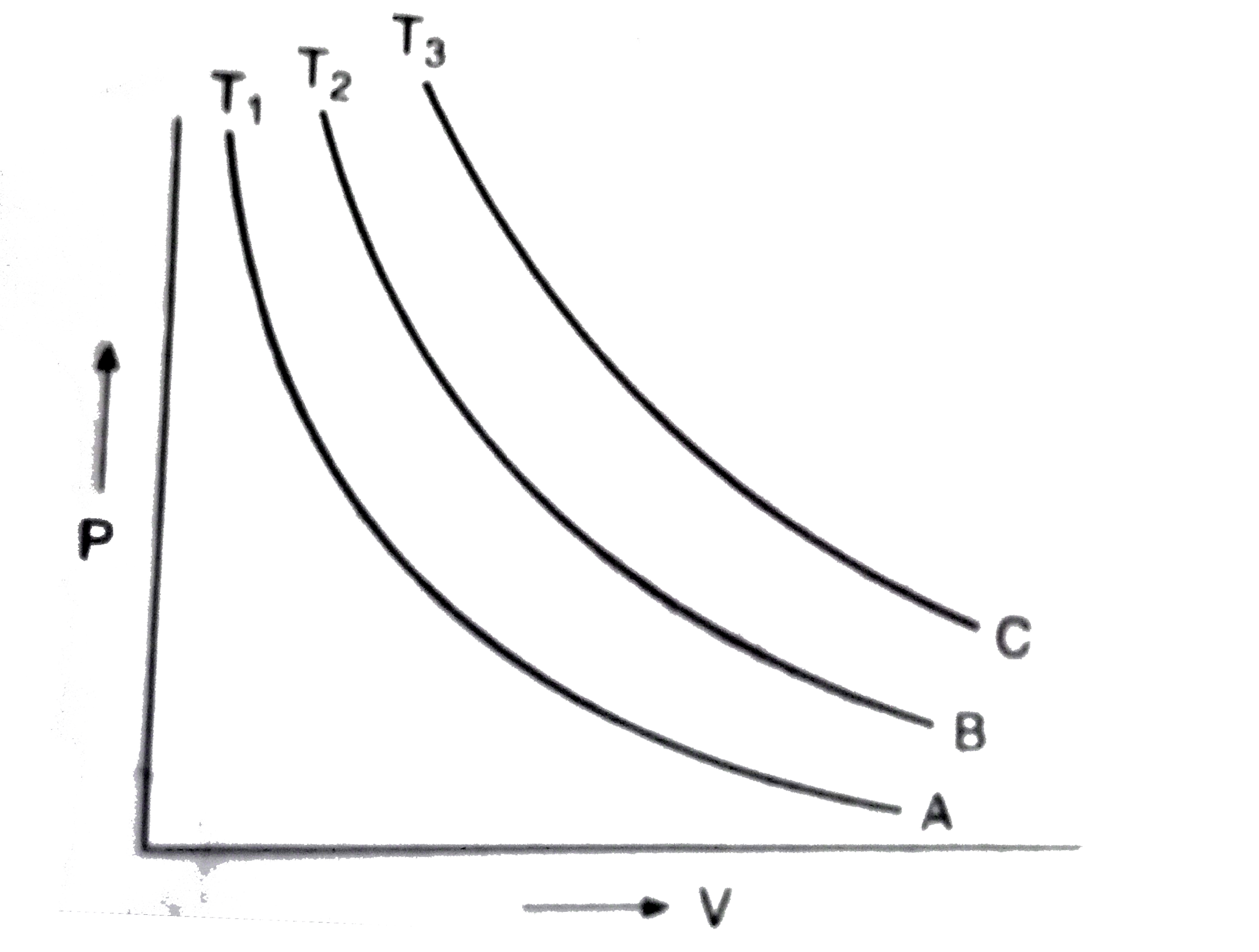A $T_{1} > T_{2} > T_{3}$
B $T_{1} > T_{3} > T_{2}$
C $T_{3} > T_{2} > T_{1}$
D $T_{3} > T_{2} > T_{2}$
The co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula $α = a T$ , where $a$ is a positive constant at T ${in}^{\circ} C$ . if the length of the rod is l at temperature $0^{\circ} C$ , then the temperature at which the length will be $2 l$ is
A $\sqrt{\frac{ln 2}{α}}$
B $\sqrt{\frac{ln 4}{α}}$
C $\frac{1}{α}$
D $\frac{2}{α}$
A calorimeter of mass m contains an equal mass of water in it. The temperature of the water and clorimeter is $t_{2} . A$ block of ice of mass m and temperature $t_{3} < 0^{\circ} C$ is gently dropped into the calorimeter. Let $C_{1}, C_{2} and C_{3}$ be the specific heats of calorimeter, water and ice respectively and $L$ be the latent heat of ice.
The whole mixture in the calorimeter becomes water if
A $(C_{1} + C_{2}) t_{2} - C_{3} t_{3} + L > 0$
B $(C_{1} + C_{2}) t_{2} + C_{3} t_{3} + L > 0$
C $(C_{1} + C_{2}) t_{2} - C_{3} t_{3} - L > 0$
D $(C_{1} + C_{2}) t_{2} + C_{3} t_{3} - L > 0$