ABC is an isosceles triangle right angled at A. forces of magnitude 2√2,5and6 act along BC, CA and AB respectively. The magnitude of their resultant force isSolution in Punjabi
4
5
11+2√2
30
The correct Answer is:B
R cosθ=6cos0∘+2√2cos(180∘−B)+5sin270∘
Rcosθ=6−2√2cosB . . (i)
Rsinθ=6sin0∘+2√2sin(180∘−B)+5sin270∘
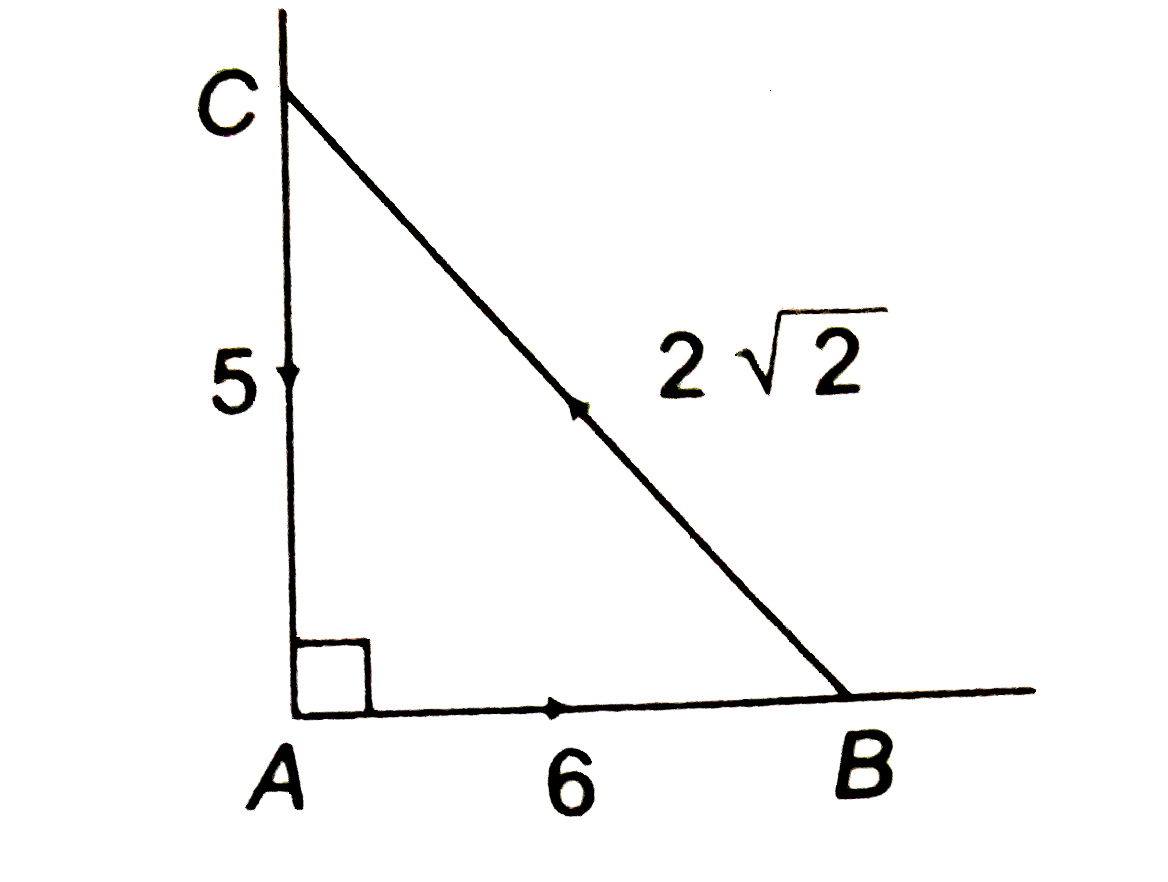
Rsinθ=2√2sinB−5 . . . (ii)
From Eqs. (i) and (ii), we get
R2=36+8cos2B−24√2cosB+8sin2B+25−20√2sinB
=61+8(cos2B+sin2B)−24√2cosB−20√2sinB
∵ ABC is a right angled isosceles triangle.
i.e., ∠B=∠C=45∘
∴R2=61+8(1)−24√21√2−20√2⋅1√2=25
∴R=5.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 17videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 217videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Classify the following measure as scalar and vector: 10Kg
04:17View SolutionIf a=2ˆi−ˆj+2ˆkandb=−ˆi+ˆj−ˆk, then find a+b. Also, find a unit vector along a+b.
02:09View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
02:12View SolutionABC is triangle,right angled at A.The resultant of the forces acting along vec AB.vec AC with magnitudes (1)/(AB) and respectively is the force along vec AB ,where D is the foot of the perpendicular from A onto BC.The magnitude of the resultant is-
01:46View SolutionForces proportional to AB , BC and 2 CA act along the slides of a triangle ABC in magnitude and direction by
05:05View SolutionThree equla force, each of magnitude P, act along the side AB, BC, and CA of a trangle. Calculate the resultant force.
06:34View SolutionForces proportional to AB, BC & 2 CA act along the sides of triangle ABC in order, their resultant represented in magnitude and direction as:
05:42View SolutionABC is isosceles triangle, right angled at A. The resultant of the forces acting along −−→AB,−−→AC with magnitudes 1AB and 1AC respectively is the force along −−→AD, where D is the foot of the perpendicular from A on BC. The magnitude of the resultant is:
04:30View SolutionABC एक समकोण त्रिभुज है −Q आवेश पर बल के परिमाण की गणना कीजिए।
 02:50View Solution
02:50View SolutionA current carrying loop in the form of a right angle isosceles triangle ABC is placed in a uniform magnetic field acting along AB. If the magnetic force on the arm BC is F, what is the force on the arm AC?
05:04View SolutionDelta ABC , But is a right angle. The forces along the AB and AC whose magnitude respectively (1)/(AB) And (1)/(AC) The resulting force of is is perpendicular to AD, where D is the length of the perpendicular from A to BC. The magnitude of the resultant force is
View SolutionA current carrying closed lop in the form of a right angle isosceles triangle ABC is placed in a uniform magnetic field acting along AB if the magnetic force on the arm BC is vecF the force on the arm AC is
02:48View SolutionABC is isosceles triangle, right angled at A. The resultant of the forces acting along −−→AB,−−→AC with magnitudes 1AB and 1AC respectively is the force along −−→AD, where D is the foot of the perpendicular from A on BC. The magnitude of the resultant is:
02:56View SolutionA current carrying closed loop in the form of a right angle isosceles triangle ABC is placed in a uniform magnetic field acting along AB. If the magnetic force on the arm BC is →F, the force on the arm AC is
 View Solution
View SolutionForces proportional to AB, BC & 2 CA act along the sides of triangle ABC in order, their resultant represented in magnitude and direction as:
View SolutionForces proportional to AB, BC and 2CA act along the sides of triangle ABC in order, their resultants represented in magnitude and direction is
02:06View Solution

