In a regular hexagon ABCDEF, prove that AB+AC+AD+AE+AF=3AD.Solution in Punjabi
The correct Answer is:B
By triangle law, AB=AD−BD,AC=AD−CD
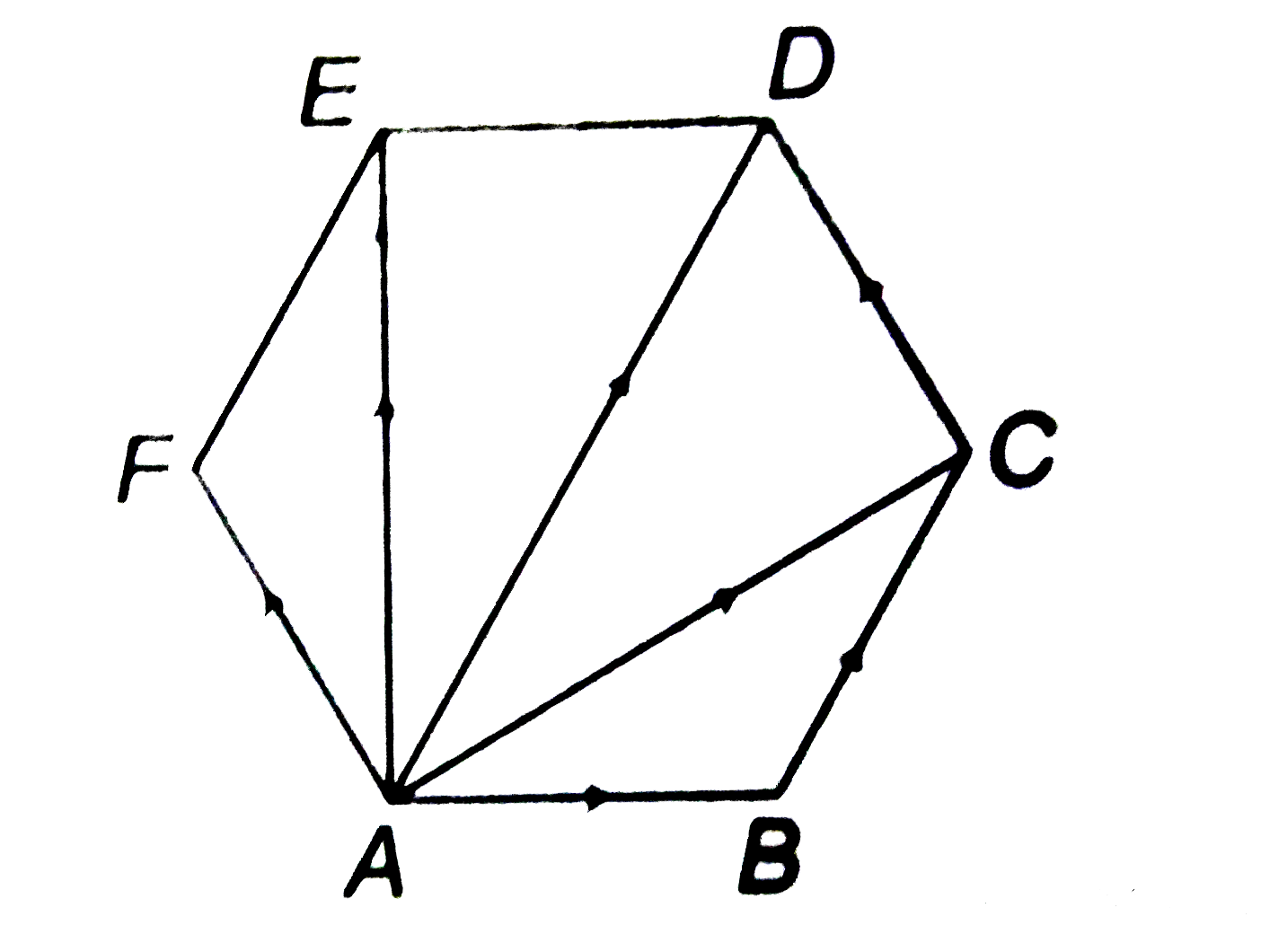
Therefore, AB+AC+AD+AE+AF
=3AD+(AE−BD)+(AF−CD)=3AD
hence, λ=3 (∵AE=BD,AF=CD)
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions1videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)7videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 311videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Find dydxify=12−x4
13:20View SolutionIf the vectors ˆi−ˆj,ˆj+ˆkand→a form a triangle then →a may be
02:40View SolutionShow that the points A(1,3,2),B(-2,0,1) and C(4,6,3) are collinear.
03:29View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
03:51View SolutionIn a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
05:04View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
03:11View SolutionConsider the regular hexagon ABCDEF with centre at O (origin).
Q. Five forces AB,AC,AD,AE,AF act at the vertex A of a regular hexagon ABCDEF. Then, their resultant is03:51View SolutionIf ABCDEF is a regular hexagon with centre O , then P.T ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=3¯¯¯¯¯¯AD=6¯¯¯¯¯¯AO
06:13View SolutionConsider the regular hexagon ABCDEF with centre at O (origin).
Five forces −−→AB,−−→AC,−−→AD,−−→AE,−−→AF act at the vertex A of a regular hexagon ABCDEF. Then their resultant is -06:20View SolutionIf ABCDEF is a regular hexagon and AB+AC+AD+AE+AF=λAD then λ is equal to
06:33View SolutionIf ABCDEF is a regular hexagon with centre O , then P.T ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=3¯¯¯¯¯¯AD=6¯¯¯¯¯¯AO
02:45View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
04:19View SolutionABCDEF is a regular hexagone. AB+AC+AD+AE+AF=λAD then λ = ………….
04:41View SolutionIn a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
03:07View SolutionConsider the regular hexagon ABCDEF with centre at O (origin).
Q. Five forces AB,AC,AD,AE,AF act at the vertex A of a regular hexagon ABCDEF. Then, their resultant is (a)3AO (b)2AO (c)4AO (d)6AO03:33View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
03:34View Solution

