A line x=λ intersects the graph of y=log5x and y=log5(x+4).The distance between the point of intersection is 0.5. Given λ=a+√b,where a and b are integers , the value of (a+b) is Solution in Punjabi
The correct Answer is:6
Step by step video & image solution for A line x=lamda intersects the graph of y=log_5x and y=log_5(x+4).The distance between the point of intersection is 0.5. Given lamda=a+sqrtb,where a and b are integers , the value of (a+b) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Matching Type Questions)
2 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise for session 8
1 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Passage Based Questions)
12 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise For Session 6
5 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
Every Integer is Natural number ?
View Solution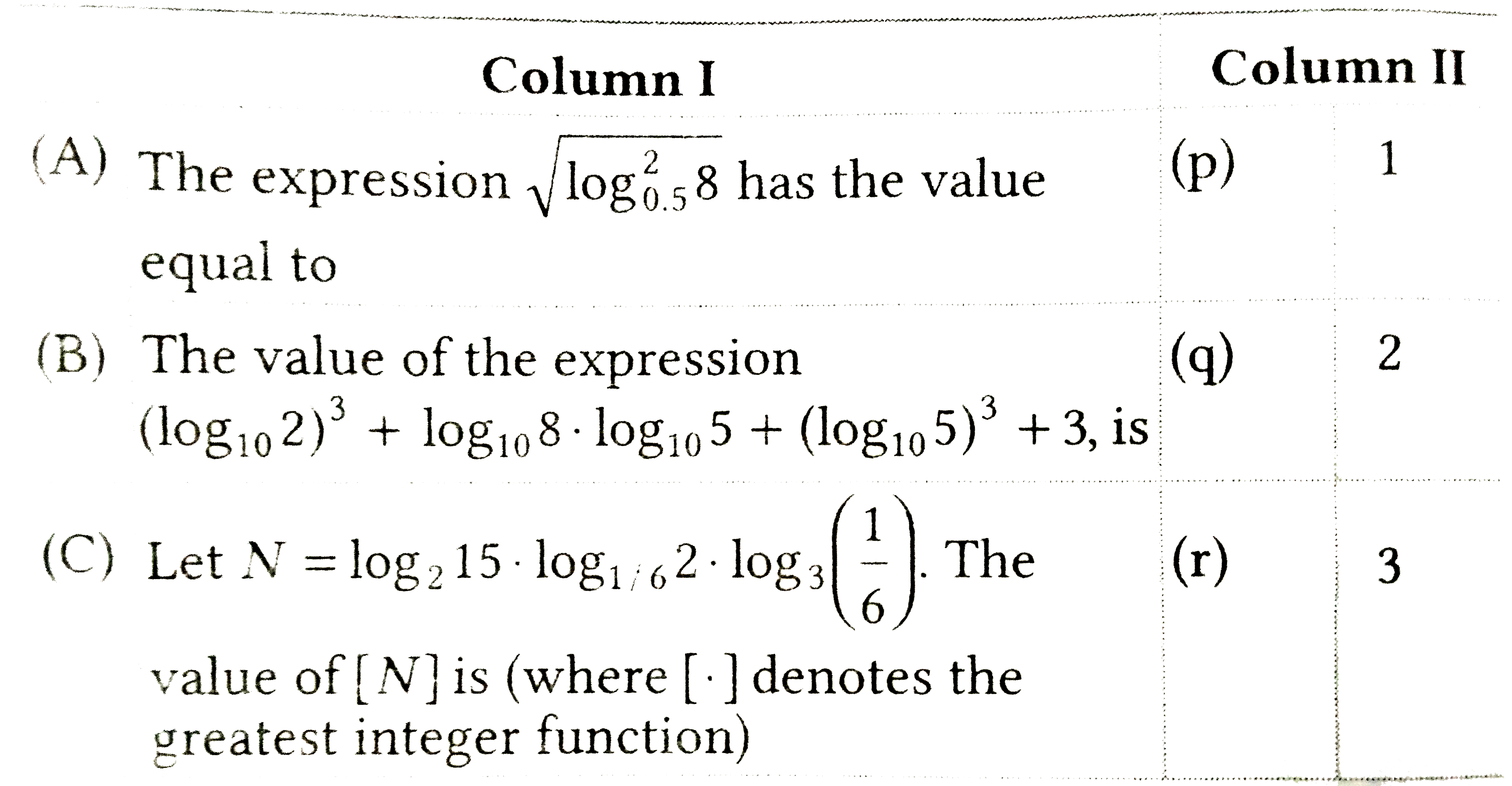
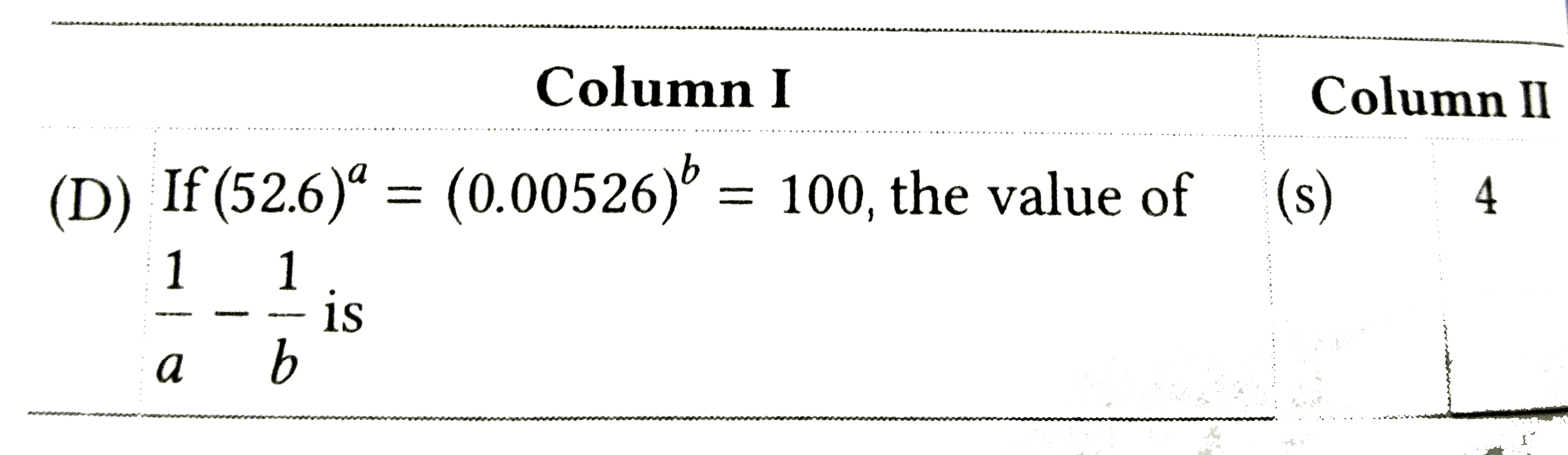
View SolutionFind dydxify=cos(logx)
View SolutionThe value o limx→∞(1n3)([12x+12]+[22x+22]+…..+[n2x+n2]) is where [.] denotes the greatest integer function.
View SolutionIf t₁+t₅+t15+t₁₀+t₂₀+t₂₄=225 Find the sum of first 24th term of that A.P?
View SolutionA line x=k intersects the graph of y=log_(4)x and y=log_(4)(x+4). The distance between the points of intersection is 0.5, then the value of k is
View SolutionIf the lines x−21=y−31=z−4λ and x−1λ=y−42=z−51 intersect then
View Solutionλ का मान ज्ञात कीजिये जिसके लिए रेखाएँ 3x+y=2,λx+2y=3 तथा 2x−y=3 एक बिंदु पर प्रतिच्छेद करती है |
View Solutionlog5x=y యొక్క ఘాత రూపం
View SolutionThe graphs of x=aandy=b intersect at
View SolutionA circle passes through the points of intersection of the lines λx−y+1=0 and x−2y+3=0 with the coordinates axes. Show that λ=2.
View SolutionIf the lines x−21=y−31=z−4λ and x−1λ=y−42=z−51 intersect then
View SolutionA line x=k intersects the graph of y=log4x and y=log4(x+4). The distance between the points of intersection is 0.5, then the value of k is
View SolutionDraw the graphs of y=x and y=−x in the same graph. Also, find the coordinates of the point where the two lines intersect.
View SolutionThe locus of the point x=a+λ2,y=b−λ where λ is a parameter is
View SolutionIf the lines x−21=y−31=z−4λandx−1λ=y−42=z−51 intersect, then
View Solution
