Find the value of t which satisfies (t−[|sinx|])!=3!5!7!where[.] denotes the greatest integer function.Solution in Punjabi
9
10
11
12
The correct Answer is:B, C
Step by step video & image solution for Find the value of t which satisfies (t-[|sin x|])! = 3!5!7! w h e r e[dot] denotes the greatest integer function. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBook:ARIHANT MATHSChapter:TRIGONOMETRIC EQUATIONS AND INEQUATIONSExercise:Exercise (Passage Based Questions)
Explore 13 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBook:ARIHANT MATHSChapter:TRIGONOMETRIC EQUATIONS AND INEQUATIONSExercise:Trigonometric Equations and Inequations Exercise 3 :Passage Based Questions
Explore 1 Video
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBook:ARIHANT MATHSChapter:TRIGONOMETRIC EQUATIONS AND INEQUATIONSExercise:Exercise (Single Option Correct Type Questions)
Explore 60 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHSChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
Explore 2 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 18 Videos
Similar Questions
If number of solution and sum of solution of the equation 3sin2x−7sinx+2=0,x∈[0,2π] are respectively N and S and fn(θ)=sinnθ+cosnθ. On the basis of above information , answer the following questions.
Value of N is
View SolutionIf an angle and a side of a right angle triangle is known , then rest of the sides and angles can be found as follows
In ΔABC(figure ), if ∠B=90∘,∠C=θandBC=x, then AB=xtanθandAC=xsecθ .
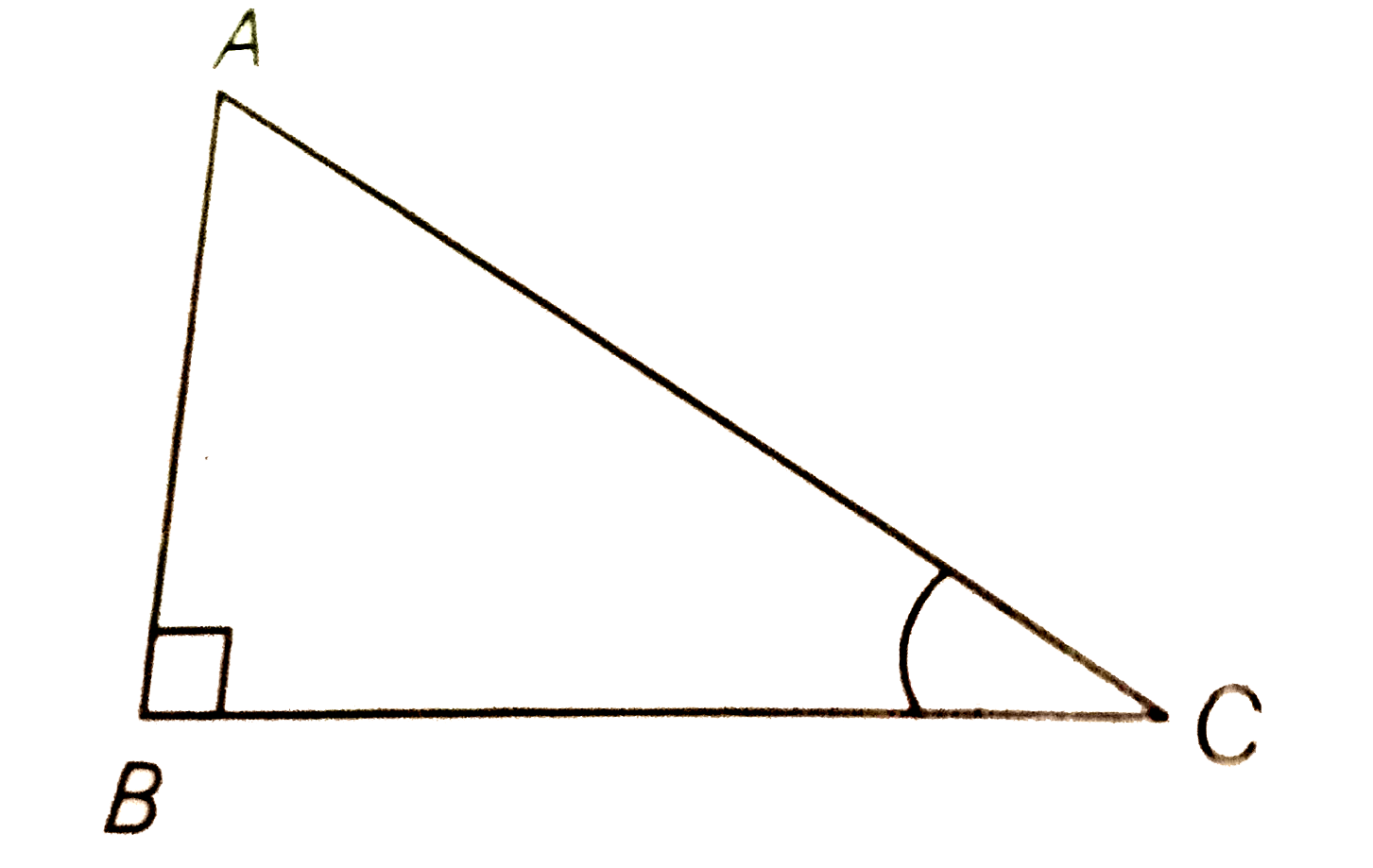
Now, consider in isosceles triangle PQR (Figure 2),
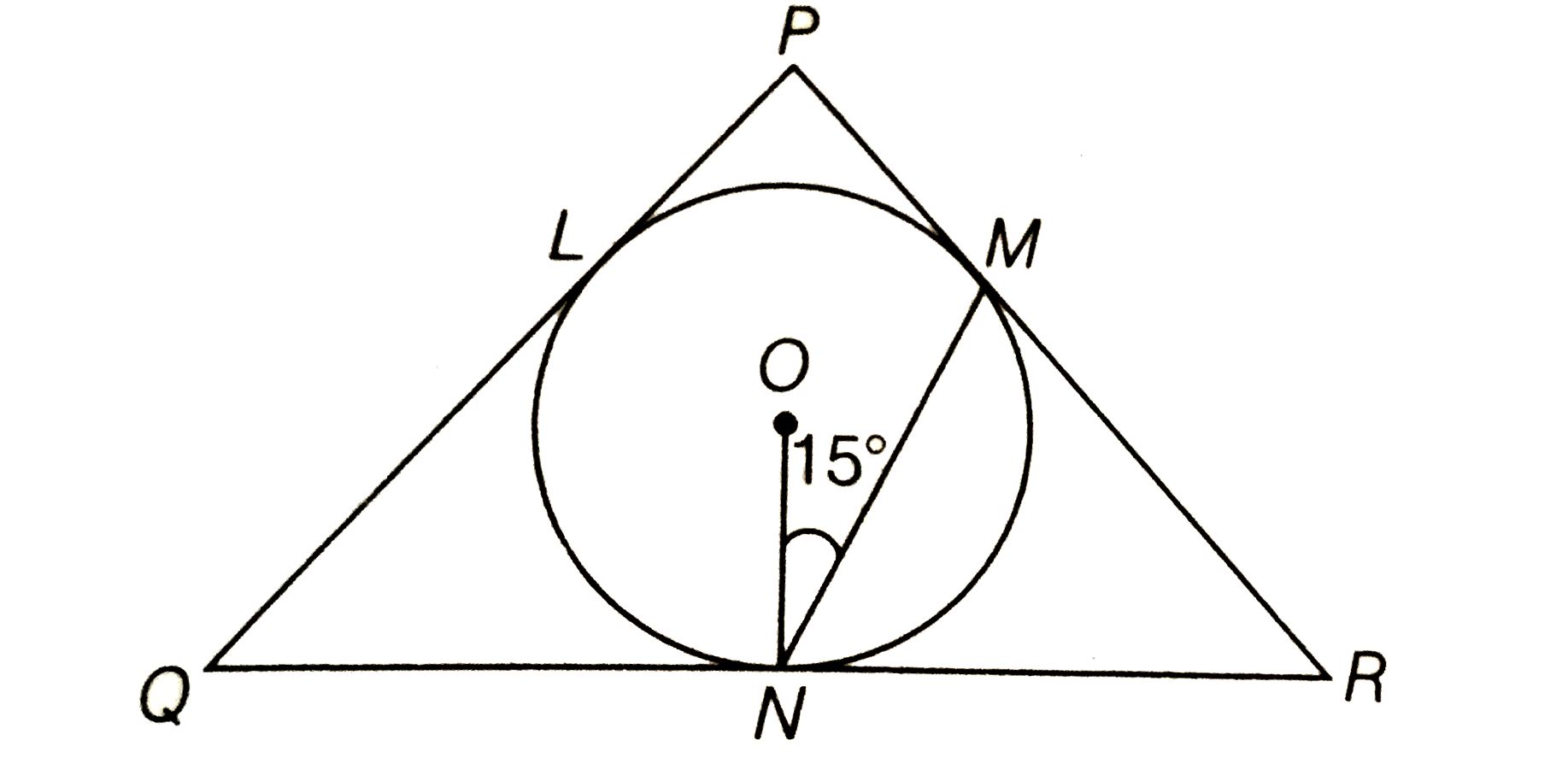
Where PQ=PR and 20N=√3
On the basis of the above information answer the question
The angle of triangle PQR are
View SolutionShow that sinx−sinycosx+cosy=tan(x−y2)
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
View SolutionFind the value of t which satisfies (t−[|sinx|])≠3!5!7!where[.] denotes the greatest integer function.
View SolutionFind the value of t which satisfies (t-[|sinx|]!=3!5! Where [.] denotes the greatest integer function.
View SolutionEvaluate: (lim)x→0sinxx,where[.] represents the greatest integer function.
View SolutionEvaluate: ∫5−5x2[x+12]dx(where[.] denotes the greatest integer function).
View Solution∫x02t2[t]dt,where[.] denotes the greatest integer function and x∈R+ , is equal to
View SolutionEvaluate: ∫e61[logx3]dx,where[.] denotes the greatest integer function.
View SolutionFind the value of : ∫100e2x−[2x]d(x−[x])where[.] denotes the greatest integer function).
View SolutionEvaluate: ∫2π0[sinx]dx,where[.] denotes the greatest integer function.
View SolutionEvaluate:- ∫π0[cotx]dx,where[.] denotes the greatest integer function.
View SolutionEvaluate: ∫1000(x−[x]dx(where[.] represents the greatest integer function).
View SolutionFind the value of : ∫100e2x−[2x]d(x−[x])where[.] denotes the greatest integer function).
View Solution
