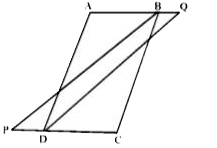
Let ABCD be a quadrilateral such that there exists a point E inside the quadrilateral satisfying AE = BE = CE = DE. Suppose is an arithmetic progression. Then the median of the set is :-
The correct Answer is:D
To solve the problem, we need to find the median of the angles ∠DAB,∠ABC,∠BCD given that they are in an arithmetic progression (AP).
1. Understanding the Angles in AP:
Since ∠DAB,∠ABC,∠BCD are in AP, we can express them as:
- Let ∠DAB=θ−α
- Let ∠ABC=θ
- Let ∠BCD=θ+α
2. Finding the Median:
The median of three numbers in AP is simply the middle term, which is ∠ABC. Thus, the median is:
Median=θ
3. Using the Property of Cyclic Quadrilaterals:
Since point E is equidistant from all vertices A,B,C,D, quadrilateral ABCD is cyclic. For a cyclic quadrilateral, the sum of opposite angles is 180∘ or π radians.
4. Finding ∠ADC:
The sum of angles in quadrilateral ABCD is 360∘ or 2π radians. Therefore:
∠DAB+∠ABC+∠BCD+∠ADC=2π
Substituting the values:
(θ−α)+θ+(θ+α)+∠ADC=2π
Simplifying this gives:
3θ+∠ADC=2π
Thus,
∠ADC=2π−3θ
5. Using the Property of Cyclic Quadrilaterals Again:
For cyclic quadrilaterals, we have:
∠ADC+∠ABC=π
Substituting ∠ADC:
(2π−3θ)+θ=π
Simplifying this gives:
2π−2θ=π
Rearranging gives:
2θ=π⟹θ=π2
6. Conclusion:
The median of the angles ∠DAB,∠ABC,∠BCD is:
θ=π2
Final Answer:
The median of the set (∠DAB,∠ABC,∠BCD) is π2.
Since ∠DAB,∠ABC,∠BCD are in AP, we can express them as:
- Let ∠DAB=θ−α
- Let ∠ABC=θ
- Let ∠BCD=θ+α
The median of three numbers in AP is simply the middle term, which is ∠ABC. Thus, the median is:
Median=θ
Since point E is equidistant from all vertices A,B,C,D, quadrilateral ABCD is cyclic. For a cyclic quadrilateral, the sum of opposite angles is 180∘ or π radians.
The sum of angles in quadrilateral ABCD is 360∘ or 2π radians. Therefore:
∠DAB+∠ABC+∠BCD+∠ADC=2π
Substituting the values:
(θ−α)+θ+(θ+α)+∠ADC=2π
Simplifying this gives:
3θ+∠ADC=2π
Thus,
∠ADC=2π−3θ
For cyclic quadrilaterals, we have:
∠ADC+∠ABC=π
Substituting ∠ADC:
(2π−3θ)+θ=π
Simplifying this gives:
2π−2θ=π
Rearranging gives:
2θ=π⟹θ=π2
The median of the angles ∠DAB,∠ABC,∠BCD is:
θ=π2
The median of the set (∠DAB,∠ABC,∠BCD) is π2.
Topper's Solved these Questions
- BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-II : MATHEMATICS7videos
QUESTION PAPER 2020
- BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-I (MATHEMATICS)20videos
QUESTION PAPER 2020
- BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( MATHEMATICS)10videos
QUESTION PAPER 2013
- BOOK - KVPY PREVIOUS YEARCHAPTER - SOLVED PAPER 2018EXERCISE - EXAMPLE27videos
SOLVED PAPER 2018
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure PAQ is the tangent of the circle at point A and ABCD is a cyclic quadrilateral.
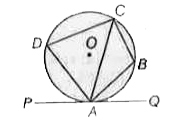
If ∠CAQ=70∘, then ∠ABC isA110∘B70∘C80∘D90∘ - Question 2 - Select One
ABCD is a cyclic quadrilateral. The tangent at A and C meet at a point P. If ∠ABC=100∘ then ∠APC will be euqal to :
A10∘B20∘C40∘D80∘ - Question 3 - Select One
ABCD is a cyclic quadrilateral whose vertices are equidistant from the point O (centre of the circle). If ∠COD=120∘ and ∠BAC=30∘, then the measure of ∠BCD is
A180∘B150∘C60∘D90∘
ABCD is a quadrilateral with right angles at AandC. Points EandF are on the diagonal AC such that DEandBF are both perpendicular to AC. If AE=3cm,DE=5cmandCE=7cm, then the length of BF is
View SolutionIn a quadrilateral ABCD, E is a point in the interior of the quadrilateral such that DE and CE are the bisector of ∠D and ∠C, respectively, If ∠B=82∘ and ∠DEC=80∘ then ∠A= ?
एक चतुर्भुज ABCD में, E, चतुर्भुज के भीतरी भाग का एक बिंदु इस प्रकार है की DE और CE क्रमश ∠D और ∠C, के द्विभाजक हैं, यदि ∠B=82∘और ∠DEC=80∘ तो ∠A = ?View SolutionABC is a triangle in which AB = AC. Let BC be produced to D. From a point E on the line AC let EF be a straight line such that EF is parallel to AB. Consider the quadrilateral ECDF thus formed. If ∠ABC=65∘ and ∠EFD=80∘, then what is ∠FDC equal to ?
View SolutionIn a quadrilateral ABCD, OA and OB are the angle bisectors of ∠DAB and ∠CBA. If ∠ADC=70∘ and ∠BCD=80∘ then find ∠AOB ?
View SolutionABCD is a cyclic quadrilateral whose vertices are equidistant from the point O (centre of the circle). If ∠COD=120∘ and ∠BAC=30∘, then the measure of ∠BCD is :
View Solution