A small coin is fixed at the center of the base of an empty of cylindrical stell container having radius R = 1 m and height d = 4 m . At time t = 0 s, the container starts gettting filled with water at a flowrate of Q=0.1m3/s without disturbing the coin . Find the approximate time when the coin will first be seen by teh observer "O" from the height of H= 5.75 m above and L = 1.5 m radially away from the coin as shown in the figure. Refractive index of water in n = 1.33
0 s
32 s
63 s
150 s
The correct Answer is:C
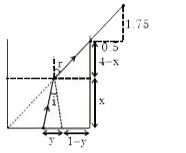
1.33sini=sinr=2√53….(i)
Also, tanr=27=1−y4−x⇒y=2x−17...(iii)<br>therefore From equation (i)
1.33y√y2+x2=2√53⇒(1.33)253y2=4(x+2y)2
⇒89.7517y2=4x2⇒y=2x√89.7517.....(iii)
From equation (ii) & (iii),
2x−17=2x√89.7517⇒14x=(2x−1)9.47
∴x=1.92
∴volume of water filled=πR2X=(3.14×12×1.92)m3
∴ Qt = 6.0288 [Q is volume flow rate]
∴ t = 60.288 sec
so option C is the nearest value
Topper's Solved these Questions
Similar Questions
A small coin is placed at the bottom of a cylindrical vessel of radius R and height h. If a transparent liquid of refractive index μ completely filled into the cylinder, find the minimum fraction of the area that should be covered in order not to see the coin.
View SolutionA coin is tossed (m+n) times (m>n). Find the probability of at least m consecutive heads.
View Solution
Knowledge Check
A small coin is fixed at the center of the base of an empty of cylindrical stell container having radius R = 1 m and height d = 4 m . At time t = 0 s, the container starts gettting filled with water at a flowrate of Q=0.1m3/s without disturbing the coin . Find the approximate time when the coin will first be seen by teh observer "O" from the height of H= 5.75 m above and L = 1.5 m radially away from the coin as shown in the figure. Refractive index of water in n = 1.33
A0 sB32 sC63 sD150 sThere are 300 coins, each coin having radius 2 cm and height 1 cm. The coins are so kept that each coin touches the other two. The base has 3 coins and the figure is built upon this base.
Find the volume of the region enclosed by the coins.A600(2√3−π)cm3B400(2√3−π)cm3C100(2√3−π)cm3D200(2√3−π)cm2A coin is tossed for a certain number of times. If the probability of getting a head is 0.4 and head appears for 24 times, find the number of times, the coin was tossed.
A120B60C40D80
The rain water from a roof of 44m×20m drains into a cylindrical tank having diameter of base 4 m height 3.5 m. If the tank is just full, find the rainfall in cm.
View SolutionRamesh has three containers.
(a) Cylindrical container A having radius r and height h,
(b) Cylindrical container B having radius 2r and height 1/2 h, and
(c) Cuboidal container C having dimensions r×r×h
The arrangement of the containers in the increasing order of their volumes is
View SolutionA coin is tossed (m+n) times, (m>n). Find the probability of getting exactly m consecutive heads.
View SolutionA coin is tossed (m+n) times, (m>n). Find the probability of getting exactly m consecutive heads.
View SolutionOil is filled in a cylindrical container up to height 4m. A small hole of area 'p' is punched in the wall of the container at a height 1.52m from the bottom. The cross sectional area of the container is Q. Ifpq=0.1 then v is (where vis the velocity of oil coming out of the hole)
View Solution