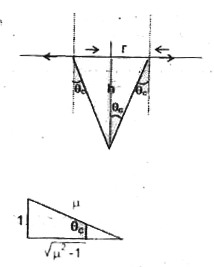
A small coin is placed at the bottom of a cylindrical vessel of radius R and height h. If a transparent liquid of refractive index $μ$ completely filled into the cylinder, find the minimum fraction of the area that should be covered in order not to see the coin.

Text Solution

Verified by Experts

When the rays coming from the coin incident at an angle $θ \geq θ_{c}$ , they will be totally reflected.
$\Rightarrow$ Minimum area that should be covered = $A = π r^{2}$ where r = radius of the circular aperture r can be found as
$r = h {tan θ}_{c}$
where $θ_{c}$ can be determined by the formula
${sin θ}_{c} = \frac{μ_{a}}{μ} = \frac{1}{μ}$
$\Rightarrow {tan θ}_{c} = \frac{1}{\sqrt{μ^{2} - 1}}$
$∴ A = π r^{2} = \frac{π h^{2}}{μ^{2} - 1}$

Updated on:21/07/2023

A cylindrical vessel of radius R and height H and open at the top is completely filled with y . A small circular hole of radius r is made near the bottom of vessel . The time taken for 25 % of water to flow out is
A $\frac{\sqrt{2 H}}{g (\sqrt{3} - 1)}$
B $\frac{R^{2}}{r^{2}} \sqrt{\frac{2 H}{g}} (1 + \frac{2}{\sqrt{3}})$
C $\frac{R^{2}}{r^{2}} \sqrt{\frac{2 H}{g}} (1 - \frac{2}{\sqrt{3}})$
D $\frac{R^{2}}{r^{2}} \sqrt{\frac{2 H}{g}} (\sqrt{3} - 1)$
A plane mirror is placed at the bottom of a tank containing a liquid of refractive index $μ$ . P is a small object at a height h above the mirror. An observes P and its image in the mirror. The apparent distance between two will be

A $2 μ h$
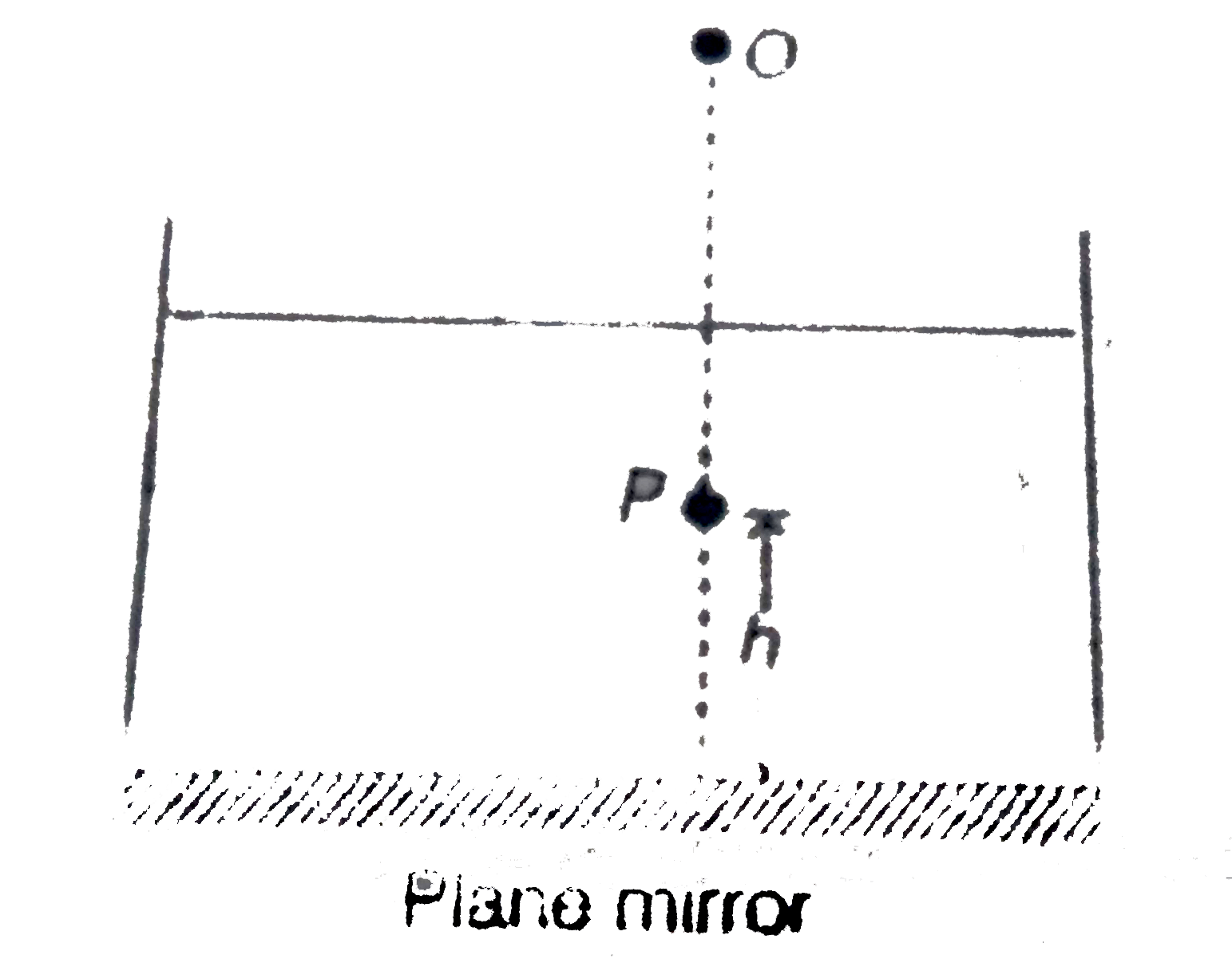B $\frac{2 h}{μ}$
C $\frac{2 h}{μ - 1}$
D $h (1 + \frac{1}{μ})$