Two identical uniform rectangular blocks (with longest side L) and a solid sphere of radius R are to be balanced at the edge of a heavy table such that the centre of the sphere remains at the maximum possible horizontal distance from the vertical edge of the table without toppling as indicated in the figure.

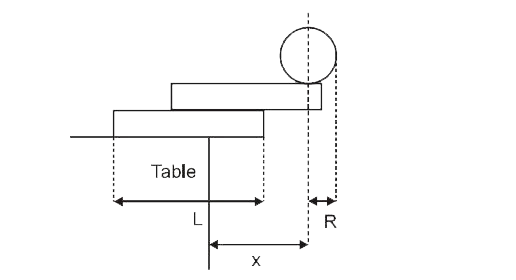
If the mass of each block is M and of the sphere is M/2, then the maximum distance x that can be achieved is

A

8L/15

B

5L/6

C

(3L/4 + R)

D

(7L/15 + R)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

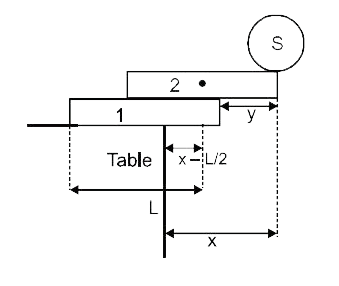
2+ S System lie above edge of 1
$\frac{M}{2} y - M (\frac{L}{2} - y) = 0$
$\frac{y}{2} + y = \frac{L}{2}$
$y = \frac{L}{3}$
Now 1 + 2 + S centre of mass will lie above the table .
$\frac{3 M}{2} (x - \frac{L}{3}) + M (x - \frac{L}{3} - \frac{L}{2}) = 0$
$\frac{3 x}{2} - \frac{L}{2} + x - \frac{L}{3} - \frac{L}{2} = 0$
$\frac{5 x}{2} = \frac{4 L}{3} x = \frac{8 L}{15}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION PAPER 2013

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
Ar
B0.5 r
C $\sqrt{0.6} r$
D $\sqrt{0.4} r$
Question 2 - Select One
A spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is

Azero
B $\frac{G M}{8 R^{2}}$
C $\frac{G M}{2 R^{2}}$
D $\frac{G M}{R^{2}}$
Question 3 - Select One
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

A $Y_{CM} = - \frac{R}{15}$
B $Y_{CM} = - \frac{R}{40}$
C $Y_{CM} = - \frac{R}{30}$
D $Y_{CM} = - \frac{R}{20}$

KVPY PREVIOUS YEAR-QUESTION PAPER 2013-PART-II (PHYSICS)

Home
Ask Doubt
Profile