Two skaters P and Q are skating towards each other. Skater P throws a ball towards W every 5 s such that it always leaves her hand with speed 2 with respect to the ground. Consider two cases:
(I) P runs with speed 1 towards Q while Q remains stationary
(II) Q runs with speed 1 towards P while P remains stationary.
Note that irrespective of speed of P, ball always leaves P's hand with speed with respect to the ground. Ignore gravity. Balls will be received by Q .
one every 2.5 s in case (I) and one every 3.3 s in case (II)
one every 2 s in case (I) and one every 4 s in case (II)
one every 3.3 s in case (I) and one every 2.5 s in case (II)
one every 2.5 s in case (I) and one every 2.5 s in case (II)
The correct Answer is:A
To solve the problem, we will analyze both cases step by step.
Case I: Skater P runs with speed 1 m/s towards Q while Q remains stationary.
1. Initial Setup:
- Let the initial distance between P and Q be x.
- Skater P throws the ball every 5 seconds with a speed of 2 m/s relative to the ground.
2. Time for the First Ball:
- The first ball is thrown at t=0 seconds.
- The time taken for the ball to reach Q can be calculated using the formula:
T1=xspeed of the ball=x2 seconds
3. Position of P after 5 seconds:
- After 5 seconds, P will have moved towards Q:
Distance covered by P=speed×time=1 m/s×5 s=5 m
- The new distance between P and Q after 5 seconds will be:
x−5 m
4. Time for the Second Ball:
- The second ball is thrown at t=5 seconds.
- The time taken for the second ball to reach Q is:
T2=x−52 seconds
5. Total Time for Each Ball:
- The total time for the first ball to reach Q is:
T1=x2
- The total time for the second ball to reach Q is:
T2=5+x−52
6. Finding the Time Difference:
- The time difference between when Q receives the first and second ball is:
T2−T1=(5+x−52)−x2
- Simplifying this gives:
T2−T1=5+x−5−x2=5−52=5−2.5=2.5 seconds
Case II: Q runs with speed 1 m/s towards P while P remains stationary.
1. Initial Setup:
- Again, let the initial distance between P and Q be x.
- The speed of the ball is still 2 m/s.
2. Time for the First Ball:
- The first ball is thrown at t=0 seconds.
- The effective speed of the ball relative to Q is:
Speed of the ball relative to Q=2+1=3 m/s
- The time taken for the first ball to reach Q is:
T1=x3 seconds
3. Position of Q after 5 seconds:
- After 5 seconds, Q will have moved towards P:
Distance covered by Q=1 m/s×5 s=5 m
- The new distance between P and Q after 5 seconds will be:
x−5 m
4. Time for the Second Ball:
- The second ball is thrown at t=5 seconds.
- The time taken for the second ball to reach Q is:
T2=x−53 seconds
5. Total Time for Each Ball:
- The total time for the first ball to reach Q is:
T1=x3
- The total time for the second ball to reach Q is:
T2=5+x−53
6. Finding the Time Difference:
- The time difference between when Q receives the first and second ball is:
T2−T1=(5+x−53)−x3
- Simplifying this gives:
T2−T1=5+x−5−x3=5−53=5−1.67=15−53=103≈3.33 seconds
Summary of Results:
- In Case I, Q receives the first ball after 2.5 seconds.
- In Case II, Q receives the first ball after 3.33 seconds.
- Let the initial distance between P and Q be x.
- Skater P throws the ball every 5 seconds with a speed of 2 m/s relative to the ground.
- The first ball is thrown at t=0 seconds.
- The time taken for the ball to reach Q can be calculated using the formula:
T1=xspeed of the ball=x2 seconds
- After 5 seconds, P will have moved towards Q:
Distance covered by P=speed×time=1 m/s×5 s=5 m
- The new distance between P and Q after 5 seconds will be:
x−5 m
- The second ball is thrown at t=5 seconds.
- The time taken for the second ball to reach Q is:
T2=x−52 seconds
- The total time for the first ball to reach Q is:
T1=x2
- The total time for the second ball to reach Q is:
T2=5+x−52
- The time difference between when Q receives the first and second ball is:
T2−T1=(5+x−52)−x2
- Simplifying this gives:
T2−T1=5+x−5−x2=5−52=5−2.5=2.5 seconds
- Again, let the initial distance between P and Q be x.
- The speed of the ball is still 2 m/s.
- The first ball is thrown at t=0 seconds.
- The effective speed of the ball relative to Q is:
Speed of the ball relative to Q=2+1=3 m/s
- The time taken for the first ball to reach Q is:
T1=x3 seconds
- After 5 seconds, Q will have moved towards P:
Distance covered by Q=1 m/s×5 s=5 m
- The new distance between P and Q after 5 seconds will be:
x−5 m
- The second ball is thrown at t=5 seconds.
- The time taken for the second ball to reach Q is:
T2=x−53 seconds
- The total time for the first ball to reach Q is:
T1=x3
- The total time for the second ball to reach Q is:
T2=5+x−53
- The time difference between when Q receives the first and second ball is:
T2−T1=(5+x−53)−x3
- Simplifying this gives:
T2−T1=5+x−5−x3=5−53=5−1.67=15−53=103≈3.33 seconds
- In Case I, Q receives the first ball after 2.5 seconds.
- In Case II, Q receives the first ball after 3.33 seconds.
Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-I ( PHYSICS)
20 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( PHYSICS)
10 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( PHYSICS)
10 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
19 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-I : PHYSICS
50 Videos
Similar Questions
An object moves with 5ms−1 toward right while the mirror moves with 1ms−1 toward the left as shown in Figure. Find the velocity of image.

View SolutionTwo persons (P) and (Q) are standing 54m apart on a long moving belt. Person (P) rolls a round staone towards person (Q) with a speed of 9ms−1 with respect to belt . If the belt is moving with a speed of 4ms−1 in the direction from (P) to (Q) (a) What will be the speed of the stone with respect to an obsever on a stationary platform if person (Q) rolls the stone with a velocity of 9ms−1 with respect to the belt towards person (P) and the time taken by the stoine to travel from (Q) to (P) ?
View Solution
Knowledge Check
Two persons start running towards each other from two points that arc 120m apart. First person ruins with a speed of 5ms−1 and the other wi9th a speed of 7ms−1. Both the persons meet after
A10 sB24 sC1 minD48 sAn observer moves towards a stationary plane mirror at a speed of 4 ms−1 . With what speed will his image move towards him?
A2ms−1B4ms−1C8ms−1Dthe image will stay at restTwo particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is
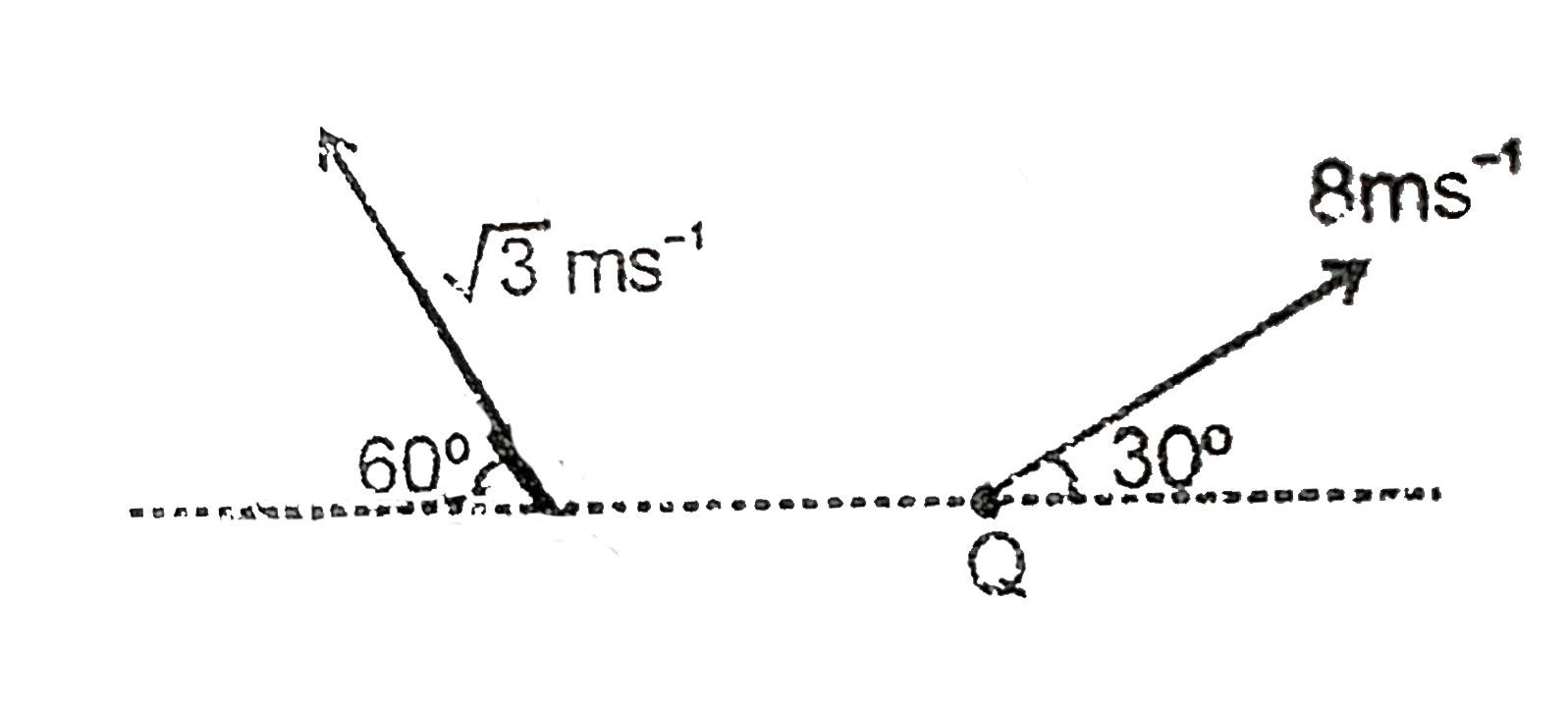 A5 rads−1B4 rads−1C2 rads−1D1 rads−1
A5 rads−1B4 rads−1C2 rads−1D1 rads−1
A ship is steaming towards east with a speed of 8 m/s. A women runs across the deck at a speed of 6ms−1 towards north. What is the velocity of the women relative to the sea ?
View SolutionAdil is running at speed of 2.5ms−1 for five minutes. He then completes the remaining distance by walking for another five minutes at speed of 1ms−1. Find the average speed of Adil.
View SolutionTwo masses of 0.25 kg each moves toward each other with speed 3 ms−1 collide and stick together. Find the final velocity
View SolutionA fish rising up vertically toward the surface of water with speed 3ms−1 observes a bird diving down vertically towards it with speed 9ms−1 . The actual velocity of bird is

View SolutionTwo particles P and Q move in a straight line AB towards each other. P starts from A with velocity u1 and an acceleration a1 Q starts they pass each other at the midpoint of AB and arrive at the other ends of AB with equal velocities.
View Solution
