If m1,m2,m3 and m4 are masses of four bodies 0.3 kg, 0.3 mg, 0.3×10−6g nad 3000 g respectively. The above in increasing order of masses are as sollows
m1>m2>m3>m4
m4>m2>m3>m4
m4>m1>m2>m3
m3>m2>m4>m1
To solve the problem of arranging the masses m1,m2,m3, and m4 in increasing order, we need to convert all the masses to the same unit. Here’s the step-by-step solution:
Step 1: Identify the masses
The given masses are:
- m1=0.3kg
- m2=0.3mg
- m3=0.3×10−6g
- m4=3000g
Step 2: Convert all masses to grams
1. Convert m1 (0.3 kg) to grams:
m1=0.3kg×1000g/kg=300g
2. Convert m2 (0.3 mg) to grams:
m2=0.3mg×10−3g/mg=0.3×10−3g=3×10−4g
3. Convert m3 (0.3 x 10−6 g) to grams:
m3=0.3×10−6g=3×10−7g
4. m4 is already in grams:
m4=3000g
Step 3: List the masses in grams
Now we have:
- m1=300g
- m2=3×10−4g
- m3=3×10−7g
- m4=3000g
Step 4: Compare the masses
To arrange them in increasing order, we compare the values:
- m3=3×10−7g (smallest)
- m2=3×10−4g
- m1=300g
- m4=3000g (largest)
Step 5: Write the increasing order
The increasing order of the masses is:
m3<m2<m1<m4
In terms of their original labels:
m3(0.3×10−6g),m2(0.3mg),m1(0.3kg),m4(3000g)
Final Answer
The increasing order of masses is:
m3<m2<m1<m4
---
The given masses are:
- m1=0.3kg
- m2=0.3mg
- m3=0.3×10−6g
- m4=3000g
1. Convert m1 (0.3 kg) to grams:
m1=0.3kg×1000g/kg=300g
m2=0.3mg×10−3g/mg=0.3×10−3g=3×10−4g
m3=0.3×10−6g=3×10−7g
m4=3000g
Now we have:
- m1=300g
- m2=3×10−4g
- m3=3×10−7g
- m4=3000g
To arrange them in increasing order, we compare the values:
- m3=3×10−7g (smallest)
- m2=3×10−4g
- m1=300g
- m4=3000g (largest)
The increasing order of the masses is:
m3<m2<m1<m4
In terms of their original labels:
m3(0.3×10−6g),m2(0.3mg),m1(0.3kg),m4(3000g)
The increasing order of masses is:
m3<m2<m1<m4
Similar Questions
Knowledge Check
Two bodies of mass 2 kg and 5 kg have position (1 m, 2 m, 1 m) and (3 m, 2 m, -1 m) respectively. The position vector of centre of mass is
A(177ˆi+2ˆj−37ˆk)mB(17ˆi+14ˆj−3ˆk)mC(2ˆi+177ˆj−37ˆk)mD(14ˆi+17ˆj−3ˆk)mTwo blocks of mass m1=6kg and m2=3kg are as shown in the diagram. Coefficient of friction between m1 and m2 and between m1 and m2 and between m1 and the surface is 0.5 and 0.4 , respectively . The maximum horizontal force that can be applied to the mass m1 so that they move without separation is
 A41NB61NC81ND101N
A41NB61NC81ND101NThe centres of three spherical masses of 1 kg, 2 kg and 3 kg have co-orinates (4,0) m,(0,3)m and (-2,5)m respectively. What is the position vector of its centre of mass is terms of its x and y co-ordinates?
A→Rcm=2ˆi+3ˆjB→RcM=13ˆi+52ˆjCveRcm=≡−13ˆi+3.5ˆjD→rcm=23ˆi−53ˆj
Four particle of masses m1=2kg,m2=4kg,m3=1kg and m4 are placed at four corners of a square as shown in figure. Can mass of m4 be adjusted I such a way that the centre of mass of system will be at the centre of the square C.
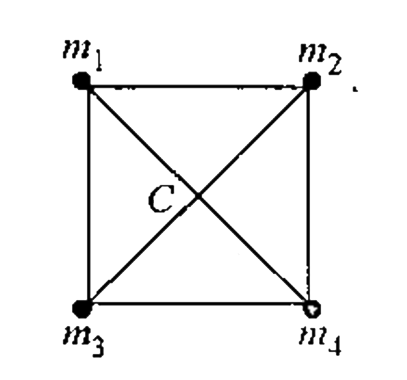
View SolutionAn aluminium wire is wound on a piece of cork of mass mcork. The densities ρcork, ρa1, and ρw, of cork, aluminium, and water are 0.5×103kg/m3,2.7×103kg/m3, and 1×103kg/ms respectively. Determine the minimum mass ma t of the wire that should be wound on the cork so that the cork with the wire is completely submerge 1 in water.
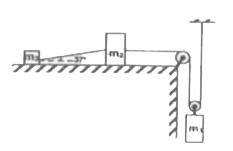
View SolutionA system consisting of light wires and blocks is released from rest as shown in figure. The coefficient of kinetic friction between the blocks and surfaces is 0.1 and masses of blocks m1,m2 & m3 are 4 kg,4kg and 2 kg respectively. The cross section of the wire between m2 and m3 is 0.003 cm2 and its Young's Modulus is 2×1011N/m2. Calculate
the acceleration of the block m2.
(b) the longitudinal strain developed in the wire m2 and m3.
View SolutionAt 800 K in a sealed vessel for the equilibrium N2(g)+O2(g)⇔2NO(g), the equilibrium concentrations of N2(g),O2(g) and NO(g) are respectively 0.36×10−3M,4.41×10−3Mand1.4×10−3M. Calculate the value of Kc for the reaction NO(g)⇔1/2N2(g)+1/2O2(g)at800Kis:
View SolutionThree blocks of masses m1,m2andm3 are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, then tension T2 will be

View Solution
