Question

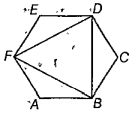
If ABCDEF is a regular hexagon, then what is the value (in degrees) of $\angle ADB$?

Options

A. 15
B. 30
C. 45
D. 60

Explanation

To find the value of angle ADB in a regular hexagon ABCDEF, we can follow these steps:

Step 1: Understand the properties of a regular hexagon.
A regular hexagon has six equal sides and six equal angles. Each internal angle of a regular hexagon can be calculated using the formula:
\( \text{Internal angle} = \frac{(n-2) \times 180}{n} \)
where \( n \) is the number of sides. For a hexagon, \( n = 6 \).

Step 2: Calculate the internal angle of the hexagon.
Substituting \( n = 6 \) into the formula:
\( \text{Internal angle} = \frac{(6-2) \times 180}{6} = \frac{4 \times 180}{6} = \frac{720}{6} = 120 \text{ degrees} \)
So, each internal angle of the regular hexagon is 120 degrees.

Step 3: Identify the points A, D, and B in the hexagon.
In the hexagon ABCDEF:
- Point A is at the top,
- Point B is to the right,
- Point D is directly across from A.

Step 4: Visualize triangle ADB.
To find angle ADB, we can observe that triangle ADB is formed by connecting points A, D, and B. Since A and B are adjacent vertices and D is directly across from A, triangle ADB is an isosceles triangle.

Step 5: Calculate angle ADB.
In triangle ADB:
- Angle ADB is the angle we want to find.
- Angles A and B are both 120 degrees (the internal angles of the hexagon).

Since the sum of angles in a triangle is 180 degrees:
\( \text{Angle A} + \text{Angle B} + \text{Angle ADB} = 180 \)
Substituting the known angles:
\( 120 + 120 + \text{Angle ADB} = 180 \)
\( 240 + \text{Angle ADB} = 180 \)
\( \text{Angle ADB} = 180 - 240 = -60 \)
Since this result doesn't make sense in the context of angles, we need to reconsider the configuration.

Step 6: Correct the approach.
Instead, we can observe that angle ADB is actually the exterior angle at point D. The exterior angle of a regular hexagon is supplementary to the internal angle:
\( \text{Exterior angle} = 180 - \text{Internal angle} = 180 - 120 = 60 \text{ degrees} \)

Final Answer:
Thus, the value of angle ADB is:
\( \text{Angle ADB} = 60 \text{ degrees} \)