In trapezium ABCD, AB||DC and CD = 2AB, EF drawn parallel to AB cuts AO in F and BC in F such that BEEC=34, diagonal DB intersects EF at Q. The find the relation between FE and AB?
9EF = 10AB
7EF = 10AB
3FE = 5AB
None of these
To solve the problem, we need to establish the relationship between the segments in trapezium ABCD, where AB is parallel to DC, and CD is twice the length of AB. We will follow these steps:
Step 1: Understand the given information
We have a trapezium ABCD with:
- AB || DC
- CD = 2AB
- EF is drawn parallel to AB, intersecting AD at F and BC at E.
- The ratio of BE to EC is given as 3:4.
Step 2: Set up the trapezium and label the lengths
Let:
- AB = x
- CD = 2x (since CD = 2AB)
- Let BE = 3k and EC = 4k for some k (from the ratio BE:EC = 3:4).
Step 3: Use the properties of parallel lines
Since EF is parallel to AB and CD, we can use the property of similar triangles. The segments created by the parallel lines will divide the non-parallel sides proportionally.
From the triangle similarity, we have:
- AF / FD = BE / EC = 3 / 4
Step 4: Express AF and FD in terms of a common variable
Let AF = 3m and FD = 4m for some m. Therefore, we can express the entire length AD as:
- AD = AF + FD = 3m + 4m = 7m.
Step 5: Establish relationships using similar triangles
From the similar triangles formed by the parallel lines:
1. Triangle DFQ ~ Triangle DAB
- DF / AD = FQ / AB
- DF / 7m = FQ / x
2. Triangle BQE ~ Triangle BDC
- QE / CD = BE / BC
- QE / 2x = 3k / (3k + 4k) = 3/7
Step 6: Solve for FQ and QE
From triangle DFQ ~ DAB:
- DF = 4m, AD = 7m
- Thus, FQ = (4/7)x
From triangle BQE ~ BDC:
- QE = (3/7)(2x) = (6/7)x
Step 7: Relate FQ and QE to EF
Since EF = FQ + QE:
- EF = (4/7)x + (6/7)x = (10/7)x
Step 8: Establish the final relationship
We can express the relationship between EF and AB:
- EF = (10/7)AB
Conclusion
Thus, the relationship between FE and AB is:
7⋅EF=10⋅AB
We have a trapezium ABCD with:
- AB || DC
- CD = 2AB
- EF is drawn parallel to AB, intersecting AD at F and BC at E.
- The ratio of BE to EC is given as 3:4.
Let:
- AB = x
- CD = 2x (since CD = 2AB)
- Let BE = 3k and EC = 4k for some k (from the ratio BE:EC = 3:4).
Since EF is parallel to AB and CD, we can use the property of similar triangles. The segments created by the parallel lines will divide the non-parallel sides proportionally.
- AF / FD = BE / EC = 3 / 4
Let AF = 3m and FD = 4m for some m. Therefore, we can express the entire length AD as:
- AD = AF + FD = 3m + 4m = 7m.
From the similar triangles formed by the parallel lines:
1. Triangle DFQ ~ Triangle DAB
- DF / AD = FQ / AB
- DF / 7m = FQ / x
- QE / CD = BE / BC
- QE / 2x = 3k / (3k + 4k) = 3/7
From triangle DFQ ~ DAB:
- DF = 4m, AD = 7m
- Thus, FQ = (4/7)x
- QE = (3/7)(2x) = (6/7)x
Since EF = FQ + QE:
- EF = (4/7)x + (6/7)x = (10/7)x
We can express the relationship between EF and AB:
- EF = (10/7)AB
Thus, the relationship between FE and AB is:
7⋅EF=10⋅AB
Topper's Solved these Questions
Similar Questions
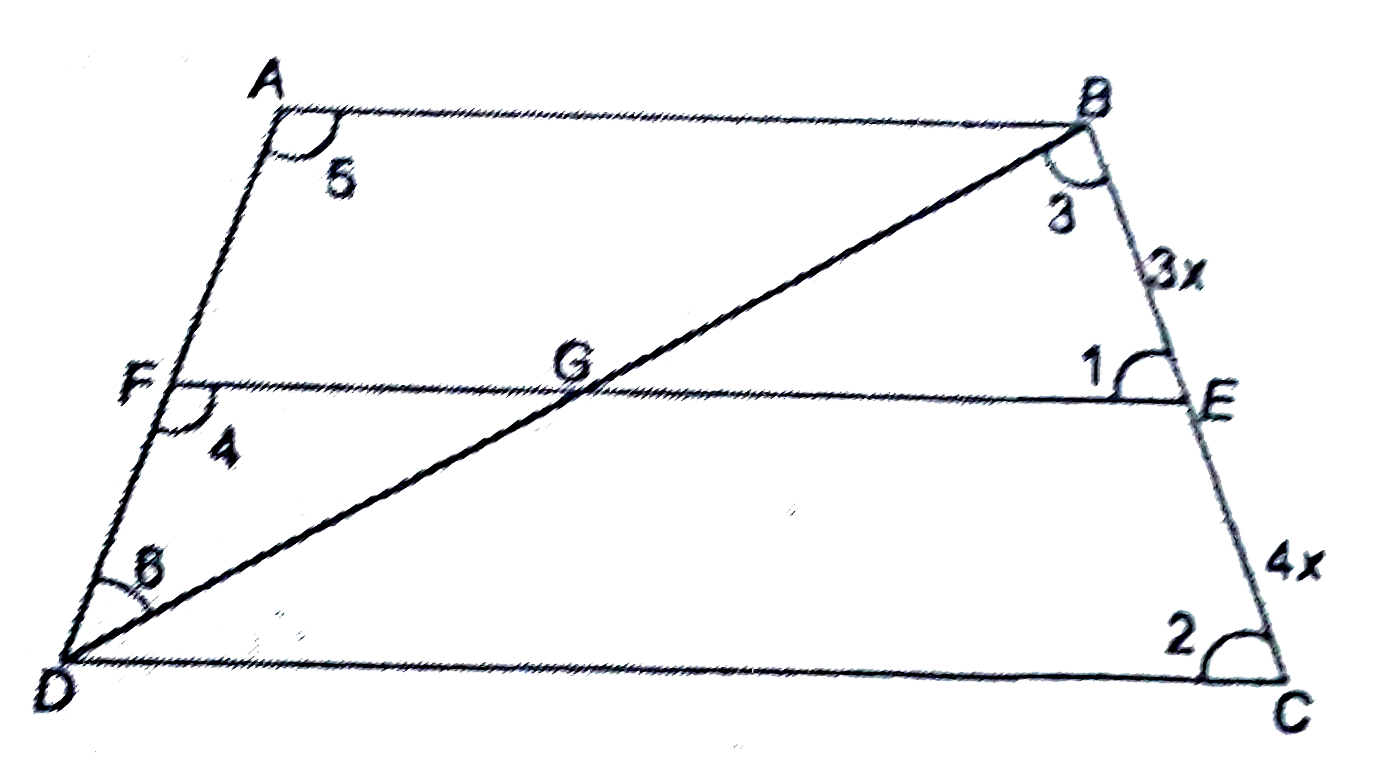
In a trapezium ABCD, AB||DC and DC=2AB. EF drawn parallel to AB cuts AD in F and BC in E such that BEBC=34 .Diagonals DB intersects EF at G. Prove that 7EF=10AB.
View SolutionIn trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parallel to AB cuts AD in F and BC in E such that BEEC=34 .
Diagonal DB intersects EF at G. prove that &EF= 10AB.
View Solution
Knowledge Check
In a trapezium ABCD ,AB||CDandDC=3AB.EF||AB intersects DA and CB at E and F such that BFFC=23 . Then 3DC=
A4EFB2EFC5EfDEFIn the given figure, AB \\ CD and EF // GH. Find the relation between a and b.
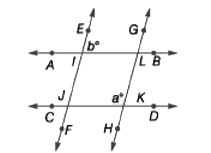 A2a +b = 180= fBa + b = 180Ca-o = 180∘Da+ 2o = 180∘
A2a +b = 180= fBa + b = 180Ca-o = 180∘Da+ 2o = 180∘
ABCD is a trapezium with AB || DC.A parallel to AC cuts the line AB at X and BC at Y. Prove that ar (ADX) = ar (ACY)
View SolutionConstruct a trapezium ABCD in which AB||DC, ∠A = 105°, AD = 3 cm, AB = 4 cm and CD = 8 cm.
View SolutionABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View SolutionABCD is a trapezium with AB||DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).
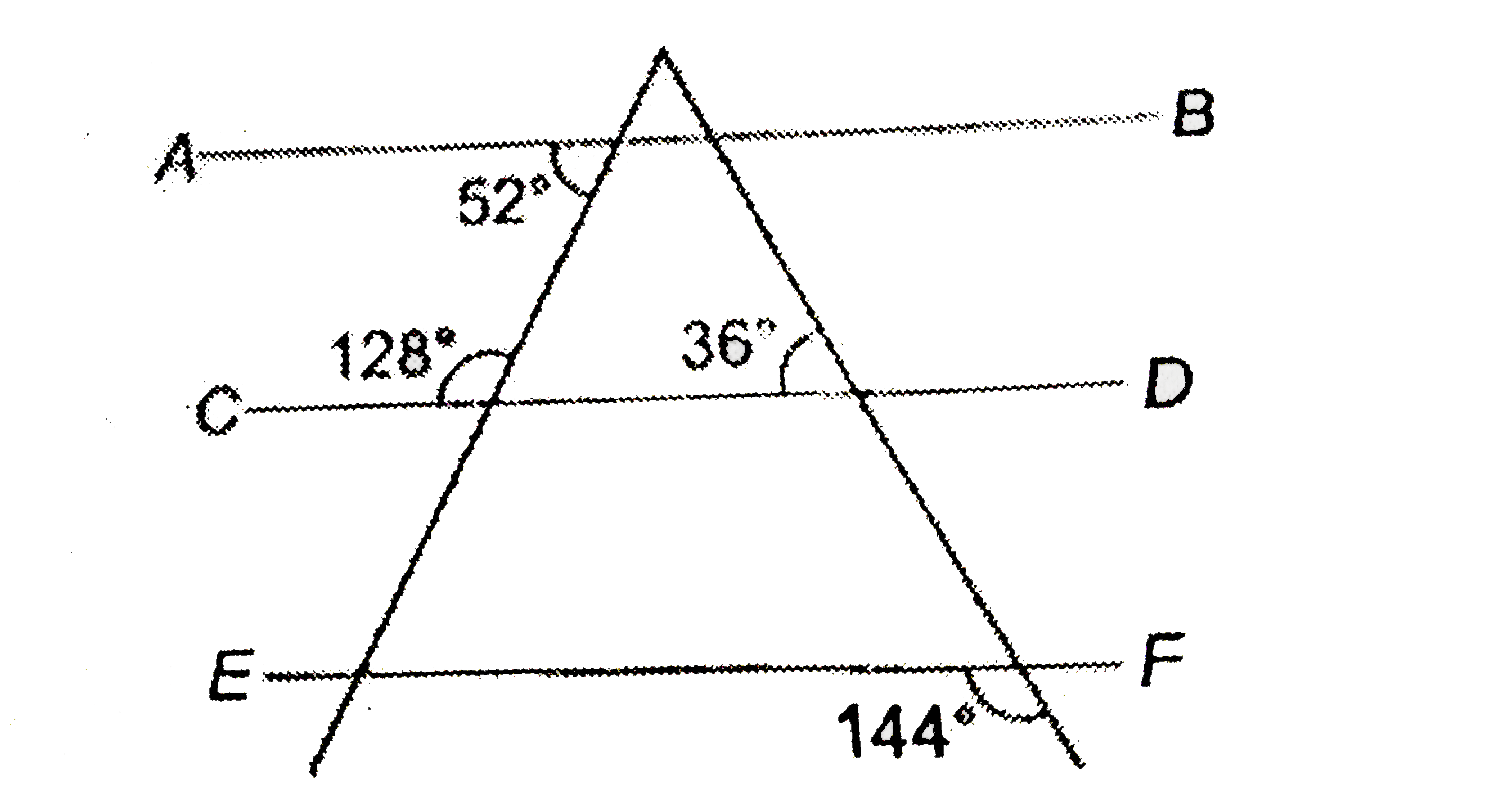
View SolutionState giving reason whether AB, CD and EF are parallel
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View Solution
