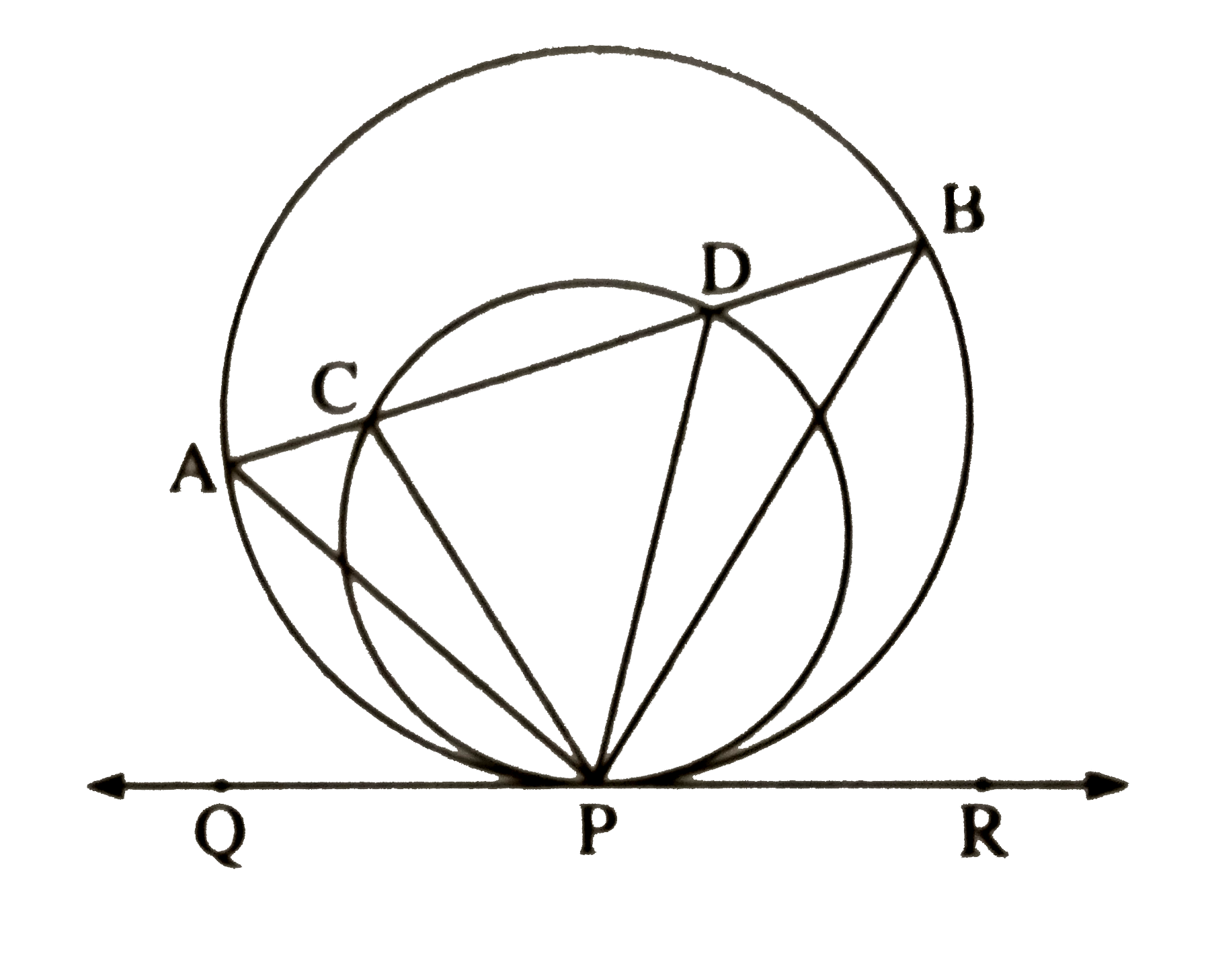
C1andC2 are two circle which touch internally at point P. Two lines PCA and PDB meet circle C1 at C and D and circle C2 at A and B respectively. If ∠BDC=120∘ then what is value of ∠ABP. (If CD||AB)
60∘
80∘
100∘
120∘
Step by step video & image solution for C_(1) and C_(2) are two circle which touch internally at point P. Two lines PCA and PDB meet circle C_(1) at C and D and circle C_(2) at A and B respectively. If angleBDC=120^(@) then what is value of angleABP. (If CD||AB) by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two circles touch each other externally at P. Two secants APB and CPD are drawn through P to meet the circle at A, C and B, D respectively. Then, which one of the following is correct ?
View SolutionIn the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
View Solution
Knowledge Check
C1andC2 are two circle which touch internally at point P. Two lines PCA and PDB meet circle C1 at C and D and circle C2 at A and B respectively. If ∠BDC=120∘ then what is value of ∠ABP. (If CD||AB)
A60∘B80∘C100∘D120∘Let C1,C2 be two circles touching each other externally at the point A and let AB be the diameter of circle C1. Draw a secant BA3 to circle C2, intersecting circle C1 at a point A1(≠A), and circle C2 at points A2 and A3 . If BA1=2, BA2=3 and BA3=4, then the radii of circles C1 and C2 are respectively
A√305,3√3010B√52,7√510C√62,√62D√103,17√1030
Given two concetric circles with centre O. A line cut the circle at A,B,C and D respectively. If AB=10cm, then find the length of CD.
View SolutionLet C1andC2 be externally tangent circles with radius 2 and 3 respectively. Let C1andC2 both touch circle C3 internally at point A and B respectively. The tangents to C3 at A and B meet at T and TA = 4, then radius of circle C3 is :
View SolutionCircles C1 and C2 are externally tangent and they are both internally tangent to the circle C3. The radii of C1 and C2 are 4 and 10, respectively and the centres of the three circles are collinear. A chord of C3 is also a common internal tangent of C1 and C2. Given that the length of the chord is m√np where m, n and p are positive integers, m and p are relatively prime and n is not divisible by the square of any prime, find the value of (m + n + p).
View SolutionIf radius of circle C1 is 2 times the radius of circle C2, then ratio of area C1 to that of C2 is
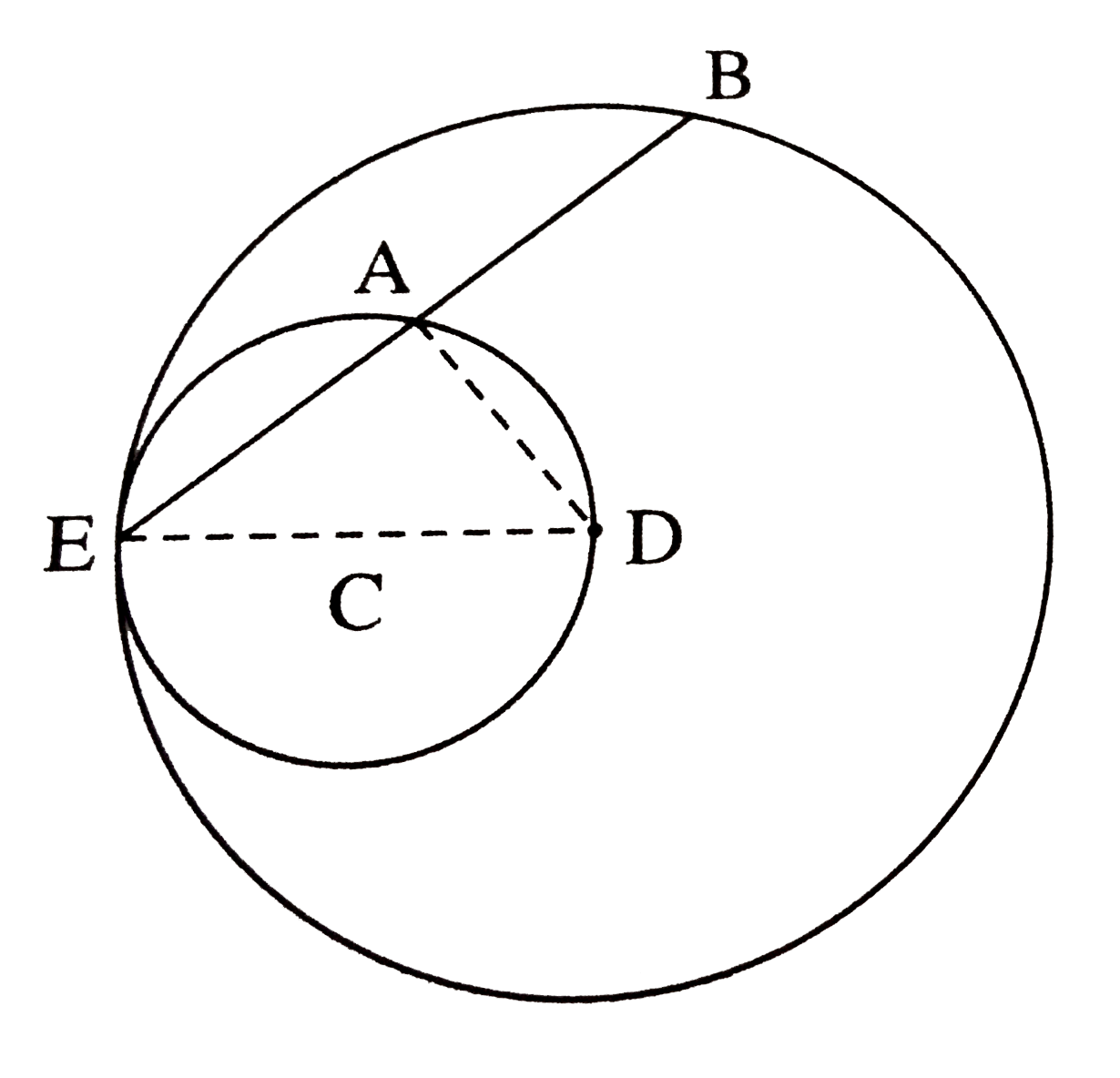
View SolutionIn figure, circles with centers C and D touch internally at point E. D lies on the inner circle. Chrd EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.
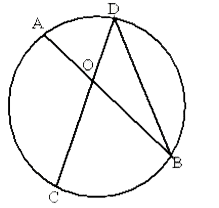
View SolutionAB is a diameter of the circle. Two points C and D are such point that CD = BD. AB and CD intersect at O. If angle ∠AOD=45∘. Find ∠ADC
View Solution
