The acceleration of a particle, moving in a straight line, at time t is (2t+1)m/sec2 . If 4m/sec is the initial velocity of the particle then its velocity after 2 sec. is
10cm/sec
8cm/sec
4cm/sec
None of these
The correct Answer is:A
To find the velocity of the particle after 2 seconds, we need to integrate the acceleration function to obtain the velocity function. Here’s the step-by-step solution:
Step 1: Write down the acceleration function
The acceleration a(t) of the particle is given by:
a(t)=2t+1(in m/s2)
Step 2: Integrate the acceleration to find the velocity
To find the velocity v(t), we integrate the acceleration function with respect to time t:
v(t)=∫a(t)dt=∫(2t+1)dt
Step 3: Perform the integration
Carrying out the integration:
v(t)=∫(2t+1)dt=2⋅t22+t+C=t2+t+C
where C is the constant of integration.
Step 4: Determine the constant of integration
We know the initial velocity v(0)=4m/s. Plugging t=0 into the velocity equation:
v(0)=02+0+C=C
Thus, C=4.
Step 5: Write the complete velocity function
Now we can write the complete velocity function:
v(t)=t2+t+4
Step 6: Calculate the velocity after 2 seconds
To find the velocity after 2 seconds, substitute t=2 into the velocity function:
v(2)=22+2+4=4+2+4=10m/s
Final Answer
The velocity of the particle after 2 seconds is:
10m/s
---
The acceleration a(t) of the particle is given by:
a(t)=2t+1(in m/s2)
To find the velocity v(t), we integrate the acceleration function with respect to time t:
v(t)=∫a(t)dt=∫(2t+1)dt
Carrying out the integration:
v(t)=∫(2t+1)dt=2⋅t22+t+C=t2+t+C
where C is the constant of integration.
We know the initial velocity v(0)=4m/s. Plugging t=0 into the velocity equation:
v(0)=02+0+C=C
Thus, C=4.
Now we can write the complete velocity function:
v(t)=t2+t+4
To find the velocity after 2 seconds, substitute t=2 into the velocity function:
v(2)=22+2+4=4+2+4=10m/s
The velocity of the particle after 2 seconds is:
10m/s
Similar Questions
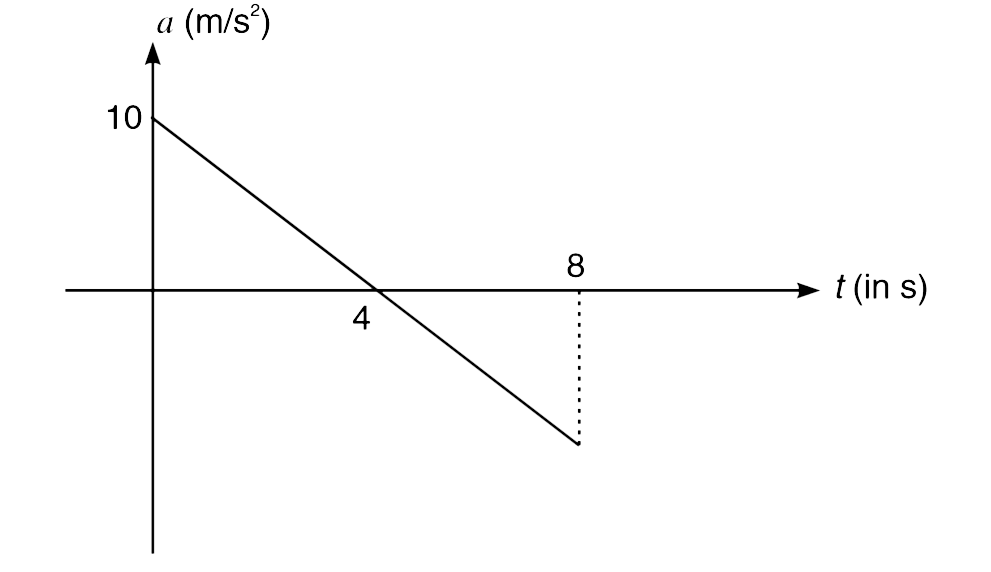
Acceleration vs time graph for a particle moving along a straight line is as shown. If the initial velocity of the particle is u=10m/s, draw a plot of its velocity vs time for 0<t<8.
View SolutionThe acceleration of a moving body at any time 't' is given by →a=(4t)ˆi+(3t2)ˆj m/sec2.If→U=0 then find the velocity of the prticle at 4 sec.
View Solution
Knowledge Check
The distance s travelled by a particle moving on a straight line in time t sec is given by s=2t3−9t2+12t+6 then the initial velocity of the particle is
A6B−9C12D11The acceleration-time graph of a particle moving in a straight line is as shown in figure. The velocity of the particle at time t=0 is 2m/s. The velocity after 2 seconds will be
 A6m/sB4m/sC2m/sD8m/s
A6m/sB4m/sC2m/sD8m/sA particle is moving on a straight line with constant retardation of 1m/s2. Its initial velocity is 10m/s.
AThe distance travelled by the particle till it comes to rest is 50 m.BThe average velocity till it comes to rest is 5m/s.CIt comes to rest in 5 sec.DIts velocity after 5 sec is 5m/s
A particle moves in a straight line as s=α(t−4)+β(t−4)2. Find the initial velocity and acceleration.
View SolutionPosition of a particle moving in a straight line is given as y = 3t^3 + t^2 (y in cm and t in second) then find acceleration of particle at t = 2sec
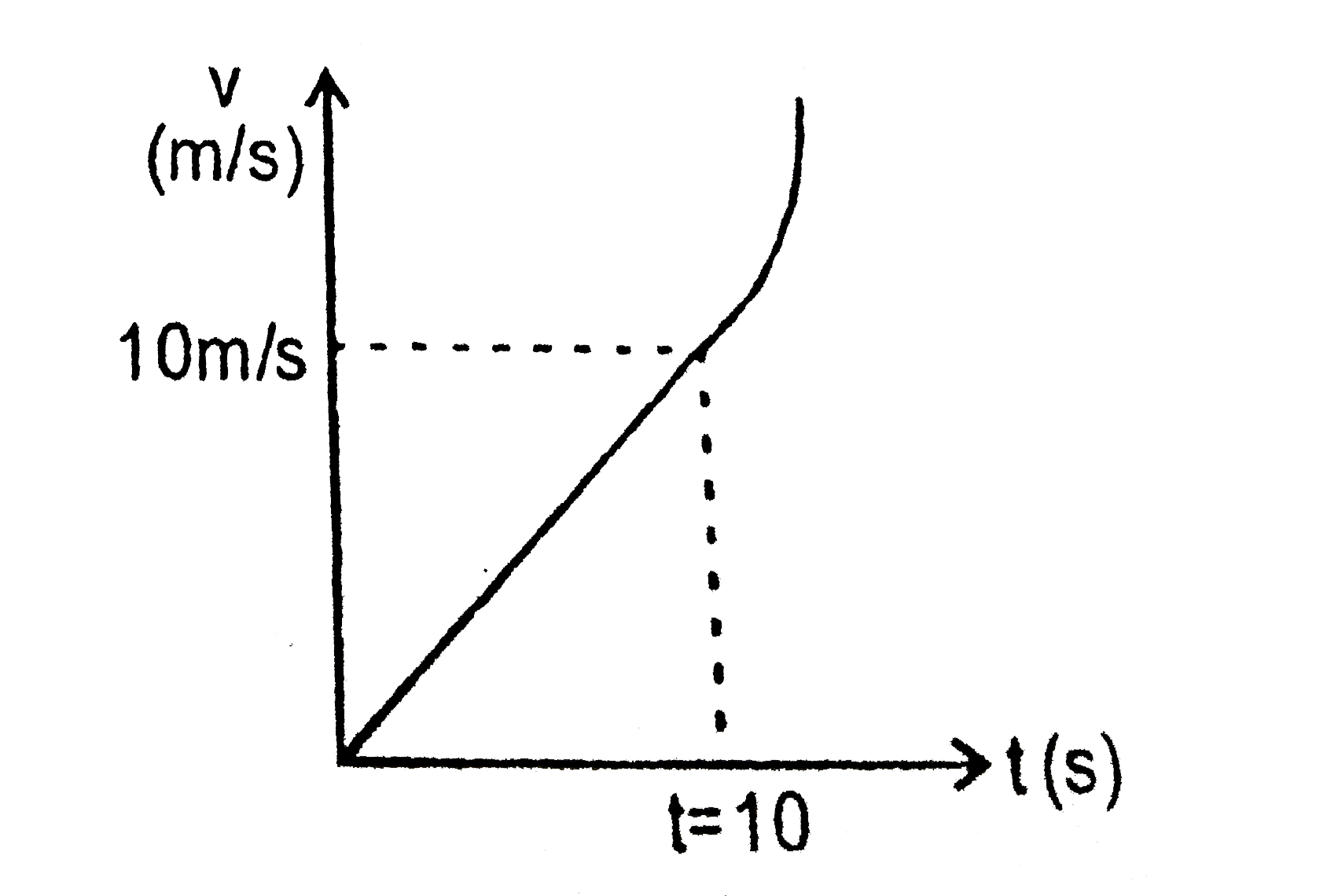
View SolutionA particle is moving in a straight line as :
a=1m/s20≤t≤10
a=2tt>10
where t is the time and a is the acceleration. If initial velocity of the particla is zero then :
View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.
View SolutionPosition of a particle moving along a straight line is given by x=2t2+t . Find the velocity at t = 2 sec.
View Solution
