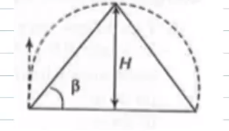
The angular elevation of any enemy's position on a hill h feet high is β. In order to shell it the velocity of the projection must not be less than [gh(1+cosecβ)]1/2.
The correct Answer is:T
Similar Questions
The angle of elevation of the top of a hill from each of the verticles A,B,C of a horizontal triangle is α. The height of the hill is 1.btanαcosecβ2.12atanαcosecA3.12ctanαcosecC 4. none of these
View SolutionA ball is projecte with a velocity 20ms−1 at an angle to the horizontal. In order to have the maximum range. Its velocity at the highest position must be
View Solution
Knowledge Check
The angular elevation of an enemy's position on a hill h feet high is β. Show that is order to shell it the initial velocity of the projectile must not be less than
A[gh(1+sinβ)]1/2B[gh(1−sinβ)]1/2C[gh(1+cosecβ)]1/2D[gh(1−cosecβ)]1/2The angular elevation of an enemy's position on a hill 'h' ft height is α.Wha should be the minimum velocity of the projectile in order to hit the enemy?
Au=√gh(cosα+1)Bu=√gh(sinα+1)Cu=√gh(cossecα+1)Du=√gh(secα+1)A ball is projecte with a velocity 20ms−1 at an angle to the horizontal. In order to have the maximum range. Its velocity at the highest position must be
A10ms−1B14ms−1C18ms−1D16ms−1
A projectile aimed at a mark, which is in the horizontal plane through the point of projection, falls a cm short of it when the elevation is α and goes b cm far when the elevation is β. Show that, if the speed of projection is same in all the cases the proper elevation is
12sin−1[bsin2α+asin2βa+b] .
View SolutionA projectile aimed at a mark, which is in the horizontal plane through the point of projection, falls a cm short of it when the elevation is α and goes b cm far when the elevation is β. Show that, if the speed of projection is same in all the cases the proper elevation is
12sin−1[bsin2α+asin2βa+b] .
View SolutionA parrticle projected with velocity u strikes at right angles a plane through the point of projection inclined at angle β to the horizon. Show that the height of the point struck above the horizontal plane through the point of projection is 2u2g.sin2β1+3sin2β and that the time of flight up to that instant is t=2ug√1+3sin2β.
View SolutionIf α,β equations are the roots of x2+px+q=0, then Make the equation whose roots have the roots of the given equation Less than h
View SolutionA shell fired from the base of a mountain just clears it. If α is the angle of projection, then the angular elevation of the summit β is
View Solution
