A ball is thrown from a point at a distance c from a smooth vertical wall and after striking against the wall it returns to the point of projection. Take 'e' to be the coefficient of restitution between the ball and the wall. If be the angle of projection with the horizontal and u the velocity of projection, then
and time of flight
The correct Answer is:T
Similar Questions
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View Solution
Knowledge Check
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is
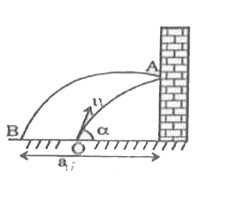 Aaeucosα,u2sin2α2gBaucosα,u2sin2α2gCaeucosα,u2sin2α2gDaucosα,u2sin2α2g
Aaeucosα,u2sin2α2gBaucosα,u2sin2α2gCaeucosα,u2sin2α2gDaucosα,u2sin2α2gA ball is projected from a point in a horizontal plane so as to strike a vertical wall at right angle A.after rebounding from the wall it strikes the horizontal plane once and returns to the point of projection just before second collision at horizontal surface. Find co-efficient of restitution for the two collisions, assuming it to be same for both the collision.
A1/2B1/3C1/4D1/5An inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
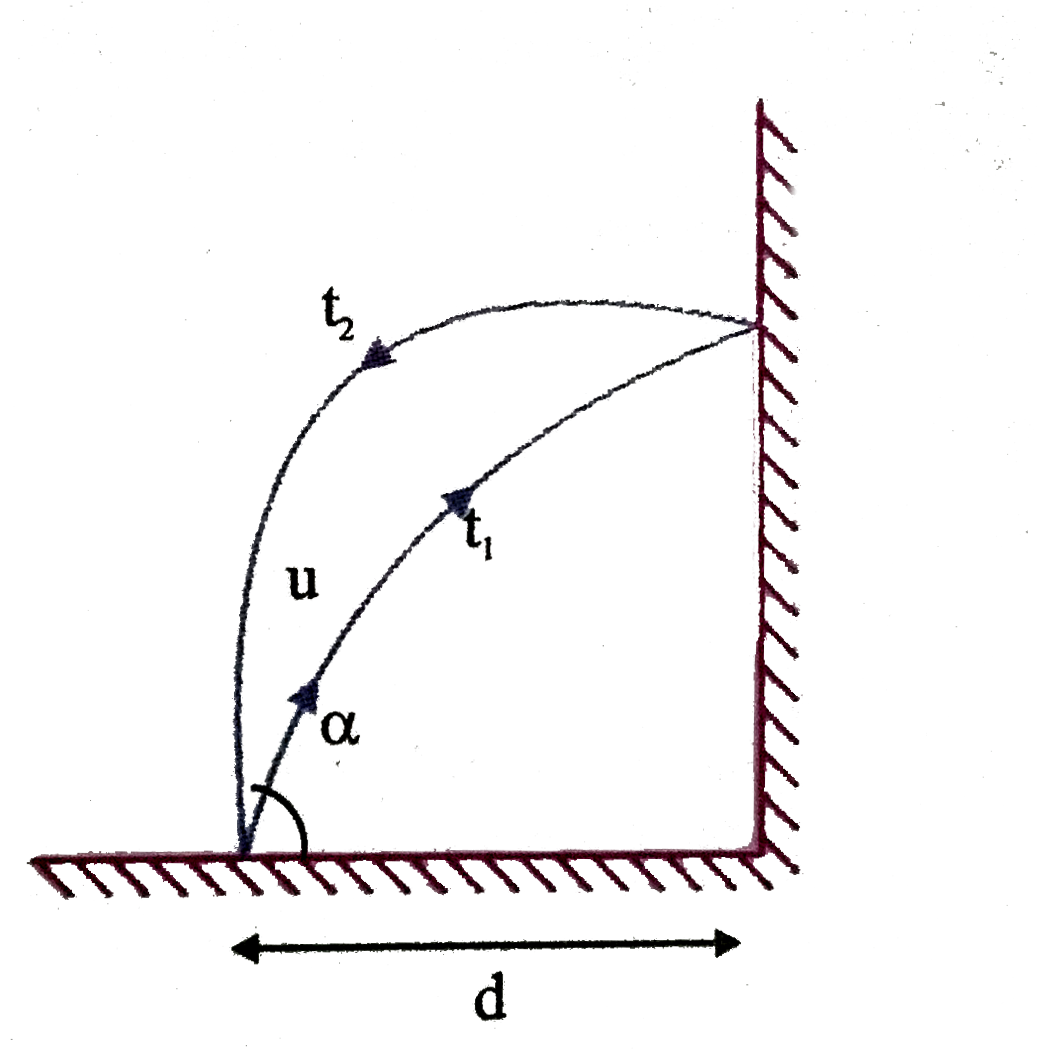
The horizontal distance 'd' from the wall isAu2sin2αg(e1+e)Bu2sinαg(e1+e)Cu2cos2αg(e1+e)Du2sin2α2g(e1+e)
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is

View SolutionA ball projected from the ground with speed 10m/s at an angle of 45∘ with horizontal. It collides with a wall at a distance 2 m from the point of projection and returns to its original position. If the coefficient of restitution between the ball and wall is 1/x, find x.
View SolutionFrom a point on a smooth floor of a room a ball is shot to hit a wall. The ball then returns back to the point of projection. If the time taken by the ball in returining is twice the time taken to reach the wall, find twice the time taken to reach the wall, find the coefficient of restitution between was and ball.
View SolutionA small ball is projected with a velocity u at some angle with horizontal towards a smooth vertical wall at a distance d from the point of projection after rebounding from the wall . If e is the coefficient of restitution then find maximum distance d for which ball may return to point of projection .
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
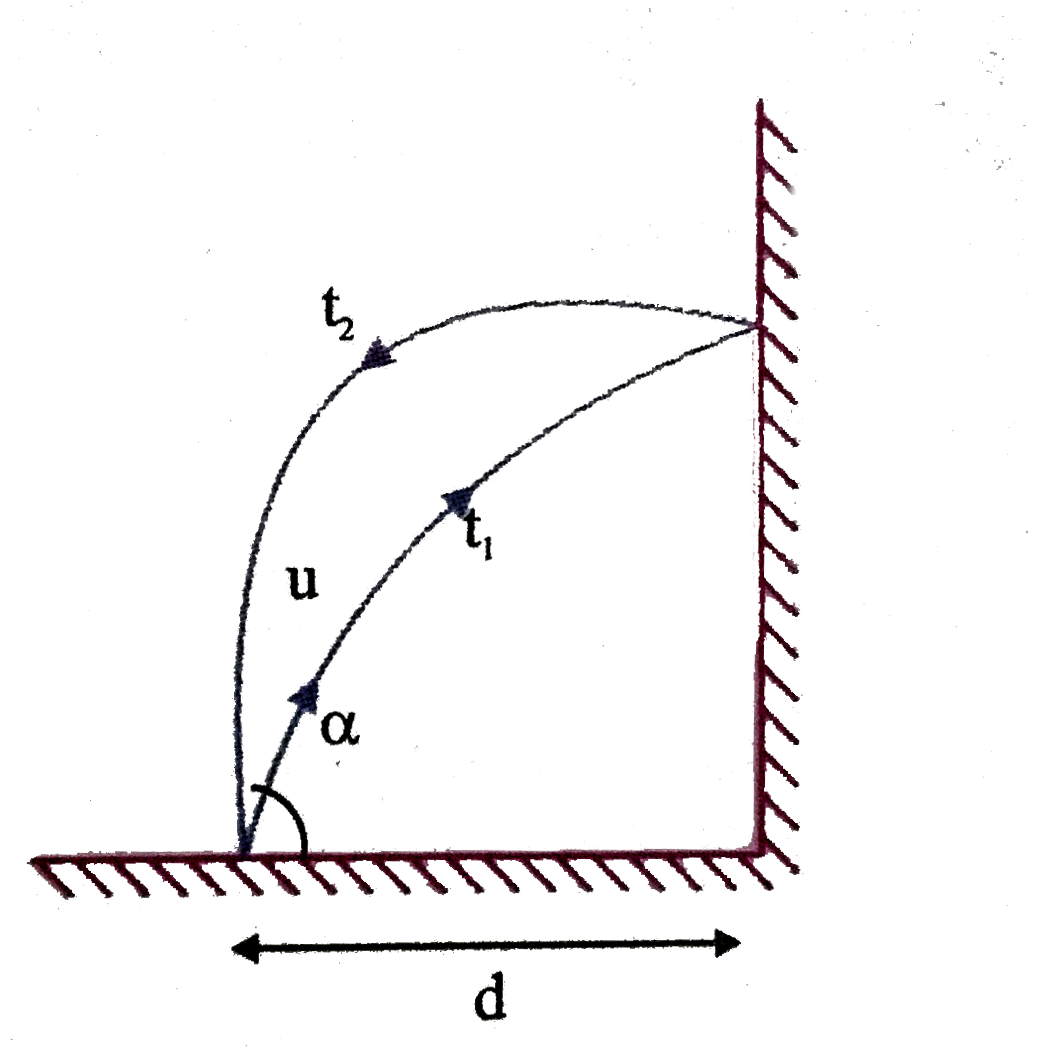
The total time of journey of the ball is
View Solution
