Obtain an expression for potential energy of the configuration of
three charges
Hence generalise the result for a system of n point charges?Solution in Punjabi

Video Solution

Text Solution

Verified by Experts

Electrostatic potential energy : Electrostatic potential energy of a system of point charges is defined as the amount of work done to bring the charges constituting the system of their respective locations.
Electrostatic potential energy of configuration of three point charges :
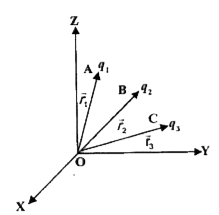
three point charges ( $q_{1}, q_{2}$ and $q_{3}$ lying at positions A, B and C.
Let ${\to r}_{1}, {\to r}_{2}$ and ${\to r}_{3}$ be the position vectors of A, B and C respectively w.r.t. the origin. Suppose initially all the three charges are at infinite distance from each other. Now move the charge $q_{1}$ from infinity to position A.
In doing so, no work has to be done because there is no electric field at A. Now move the charge $q_{2}$ from infinity to point B. In doing so, work done is given by
$W_{12} =$ (Potential at B due to $q_{1}$ at A) $\times q_{2}$
$W_{12} = \frac{1}{4 π \in_{0}} \frac{q_{1} q_{2}}{r_{12}}$
where $r_{12}$ is the distance between $q_{1}$ and $q_{2}$ .
Now move the charge $q_{3}$ from infinity to C.
But there will be some potential at C due to $q_{1}$ and $q_{2}$ lying at A and B. In doing so work done is given by
$W_{13}$ = (Potential at C due to $q_{1}$ ) $\times q_{3}$
$W_{13} = \frac{1}{4 π \in_{0}} \frac{q_{1} q_{3}}{r_{13}}$
$W_{23}$ = ( Potential at C due to $q_{2}$ ) $\times q_{3}$
and $W_{23} = \frac{1}{4 π \in_{0}} \frac{q_{2} q_{3}}{r_{23}}$
Thus total work done to bring all the three charges at their respective locations is given by
$W = W_{12} + W_{13} + W_{23}$
or $W = \frac{1}{4 π \in_{0}} (\frac{q_{1} q_{2}}{r_{12}} + \frac{q_{1} q_{3}}{r_{13}} + \frac{q_{2} q_{3}}{r_{23}})$
This work is stored in the system in the form of its electric P.E.
$∴ U = \frac{1}{4 π \in_{0}} (\frac{q_{1} q_{2}}{r_{12}} + \frac{q_{1} q_{3}}{r_{13}} + \frac{q_{2} q_{3}}{r_{23}})$
$U = \frac{1}{2} [\frac{1}{4 π \in_{0}} 3 \sum i = 1 3 \sum j = 1 \frac{q_{i} q_{j}}{r_{i j}}]$

The factor $\frac{1}{2}$ is introduced because each term counted twice in the above way of writing the expression.
Electric potential energy due to a system of n point charges
Let $q_{1}, q_{2}, q_{3}, q_{4}, ... ... . . q_{n}$ be the n point charges lying in space having position vectors ${\to r}_{1}, {\to r}_{2}, {\to r}_{4} ... ... . {\to r}_{n}$
Electrostatic potential energy of the system of n charges is given as
$U = \frac{1}{2} ⎡ ⎢ ⎢ ⎢ ⎣ \frac{1}{4 π \in_{0}} n \sum i = 1 \sum i = j i \neq j \frac{q_{i} q_{j}}{r_{i j}} ⎤ ⎥ ⎥ ⎥ ⎦$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATIC POTENTIAL

Topper's Solved these Questions

Similar Questions

BETTER CHOICE PUBLICATION-ELECTROSTATIC POTENTIAL-LONG ANSWERTYPE QUESTIONS (5/6 Marks Questions)

Home
Ask Doubt
Profile