Obtain an expression for potential energy due to a collectrion of three point charges which are separated by finite distances.

Text Solution

Verified by Experts

Electrostatic potential energy for collection of point charges : The electric potential at a point at a distance r from charge $q_{1}$ is given by
$V = \frac{1}{4 π ε_{0}} \frac{q_{1}}{r}$
This potential V is the work done to bring a unit positive charge from infinity at a distance r from $q_{1}$ the work done is the product of $q_{2}$ and the electric potential at that point. Thus we have $W = q_{2} V$
This work done is stored as the electrostatic potential energy U of a system of charge $q_{1}$ and $q_{2}$ separated by a distance r. Thus we have
$U = q_{2} V = \frac{1}{4 π ε_{0}} \frac{q_{1}}{q_{2}} / (r)$
The electrostatic potential energy depends only on the distance between the two point charges . In fact the expression (3) is derived by assuming that $q_{1}$ is fixed and $q_{2}$ is brought from infinity. The equation (3) holds true when $q_{2}$ is fixed and $q_{1}$ is brought from infinity or both $q_{1}$ and $q_{2}$ are simultaneously brought from infinity to a distance r between them . Three charges are arranged in the following configuration as shown in Figure . To calculate the total electrostatic potential energy we use the following procedure . We bring all the charges one by one and arrange them according to the configuration .

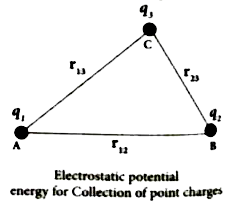
(i) Bringing a charge $q_{1}$ from infinity to the point A requires no work because there are no other charges already present in the vicinity of charge $q_{1}$ .
(ii) To bring the second charge $q_{2}$ to the point B work must be done against the electric field created by the charge $q_{1}$ . So the work done on the charge $q_{2}$ is W= $q_{2} V_{1 B} .$ Here $V_{1 B}$ is the electrostatic potential due to the charge $q_{1}$ at point B.
$U = \frac{1}{4 π ε_{0}} \frac{q_{2} q_{2}}{r_{12}}$
Note that the expression is same when $q_{2}$ is brought first and then $q_{1}$ later.
(iii) Similarly to bring the charge $q_{3}$ to the point C work has to be done against the total electric field due to both charges $q_{1}$ and $q_{2}$ . So the work done to bring the charge $q_{3}$ is = $q_{3} (V_{1 C} + V_{2 C}) .$ Here $V_{1 C}$ is the electrostatic potential due to charge $q_{1}$ at point C and $V_{2 c}$ is the electrostatic potential due to charge $q_{2}$ at point C .
The electrostatic potential is
$U = \frac{1}{4 π ε_{0}} (\frac{q_{1} q_{3}}{r_{13}} + \frac{q_{2} q_{3}}{r_{23}})$
(iv) Ading equations (4) and (5) the total electrostaic potential for the system of three charges $q_{1}, q_{2}$ and $q_{3}$ is
$U = \frac{1}{4 π ε_{0}} (\frac{q_{1} q_{2}}{r_{12}} + \frac{q_{1} q_{3}}{r_{13}} + \frac{q_{2} q_{3}}{r_{23}})$
Note that this stored potential energy U is equal to the total external work done to asemble the three charges at the given locations . The epression (6) is same if the charges are brought to their poitions in any other order. Since the Coulomb force is a conservative force the electrostatic potential energy is independent of the manner in which the configuration of charges is arrived at .

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two equal and opposite charges separated by a finite distance is
Aelectric dipole
Belectric torque
Celectric dipole moment
Dnone of these

FULL MARKS-ELECTROSTATICS -Textual Evaluation Solved ( III. Long Answer Questions: )

Home
Ask Doubt
Profile