If the density of the material increase, the value of young's modulus
increases
decreases
first increases, then decreases
first decreases, then increases
The correct Answer is:A
To determine how the value of Young's modulus changes with an increase in the density of a material, we can follow these steps:
Step 1: Understand Young's Modulus
Young's modulus (Y) is defined as the ratio of stress (force per unit area) to strain (change in length per original length) in a material. The formula for Young's modulus is given by:
Y=F⋅LA⋅ΔL
where:
- F = force applied,
- L = original length of the material,
- A = cross-sectional area,
- ΔL = change in length.
Step 2: Rearranging the Formula
We can manipulate the formula to express it in terms of volume. We know that:
Volume(V)=A⋅L
Thus, we can express the area A in terms of volume:
A=VL
Substituting this back into the Young's modulus equation gives:
Y=F⋅L(VL)⋅ΔL=F⋅L2V⋅ΔL
Step 3: Relate Volume to Density
Density (ρ) is defined as:
ρ=mV
where m is the mass of the material. Rearranging gives:
V=mρ
Substituting this expression for volume into the Young's modulus equation results in:
Y=F⋅L2⋅ρm⋅ΔL
Step 4: Analyze the Relationship
From the equation derived, we can see that Young's modulus is directly proportional to the density (ρ). This means that as the density of the material increases, the value of Young's modulus also increases, assuming that the force, length, and change in length remain constant.
Conclusion
Therefore, if the density of the material increases, the value of Young's modulus also increases.
Final Answer
The correct answer is: Young's modulus increases with an increase in density.
---
Young's modulus (Y) is defined as the ratio of stress (force per unit area) to strain (change in length per original length) in a material. The formula for Young's modulus is given by:
Y=F⋅LA⋅ΔL
where:
- F = force applied,
- L = original length of the material,
- A = cross-sectional area,
- ΔL = change in length.
We can manipulate the formula to express it in terms of volume. We know that:
Volume(V)=A⋅L
Thus, we can express the area A in terms of volume:
A=VL
Substituting this back into the Young's modulus equation gives:
Y=F⋅L(VL)⋅ΔL=F⋅L2V⋅ΔL
Density (ρ) is defined as:
ρ=mV
where m is the mass of the material. Rearranging gives:
V=mρ
Substituting this expression for volume into the Young's modulus equation results in:
Y=F⋅L2⋅ρm⋅ΔL
From the equation derived, we can see that Young's modulus is directly proportional to the density (ρ). This means that as the density of the material increases, the value of Young's modulus also increases, assuming that the force, length, and change in length remain constant.
Therefore, if the density of the material increases, the value of Young's modulus also increases.
The correct answer is: Young's modulus increases with an increase in density.
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)
40 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
On applying a stress of xN/m2, the length of wire of some material gets doubled. Value of Young's modulus for the material of wire in N/m2, is (assume Hooke's law to be valid and go for approx. results)
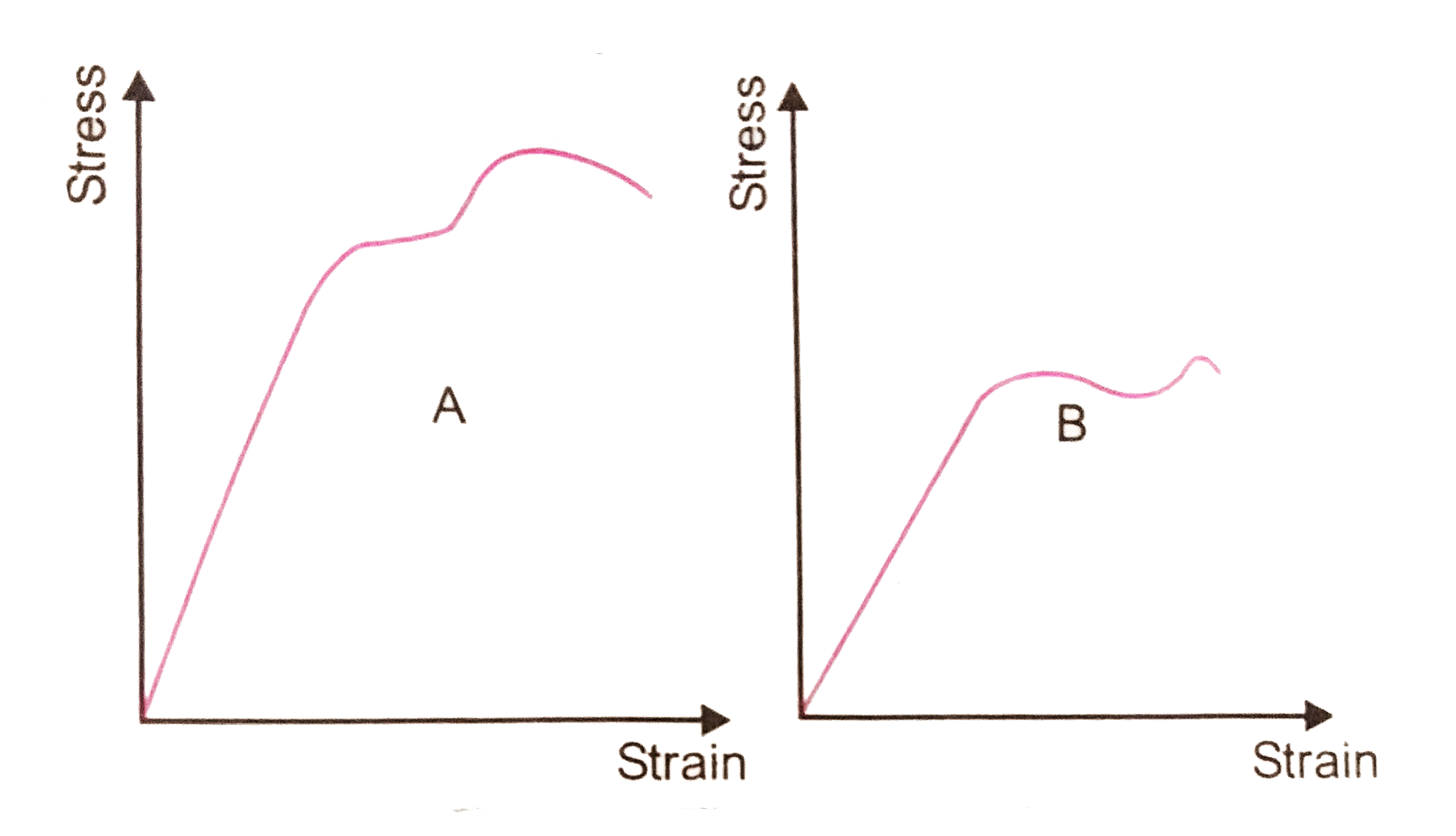
View SolutionIn the figure shown the straing versus stress graph for two values of young's modulus ?
(i) which material is more ductile ? Explain.
(ii) Which material is more brittle ? Explain.
(iii) Which material is stronger ? Explain.
View Solution
Knowledge Check
Which of the following substances has highest value of Young's modulus?
AAluminiumBIronCCopperDSteel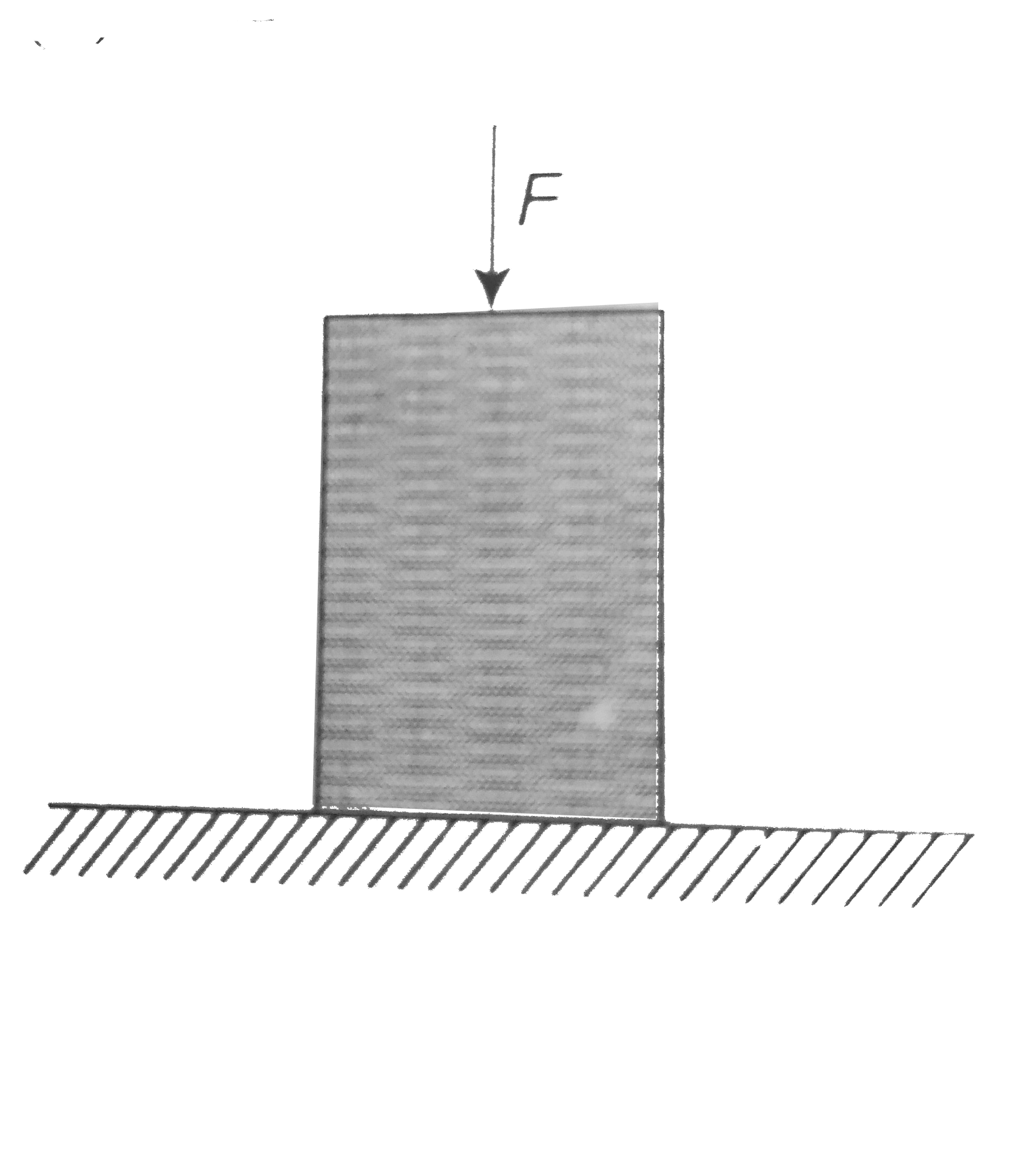
A metal cylinder of length L is subjected to a uniform compressive to a uniform compressive force F as shown in the figure. The material of the cylinder has Young's modulus Y and poisson's ratio σ The change in volume of the cylinder isAsigamFLYB(1−σ)FLYC(1+2σ)FLYD(1−2σ)FLY
In the figure shown the straing versus stress graph for two values of young's modulus ?

(i) which material is more ductile ? Explain.
(ii) Which material is more brittle ? Explain.
(iii) Which material is stronger ? Explain.
View SolutionIf the load of a wire is increases such that its stress is twice as that of previous, then the new value of Youngs modulus is
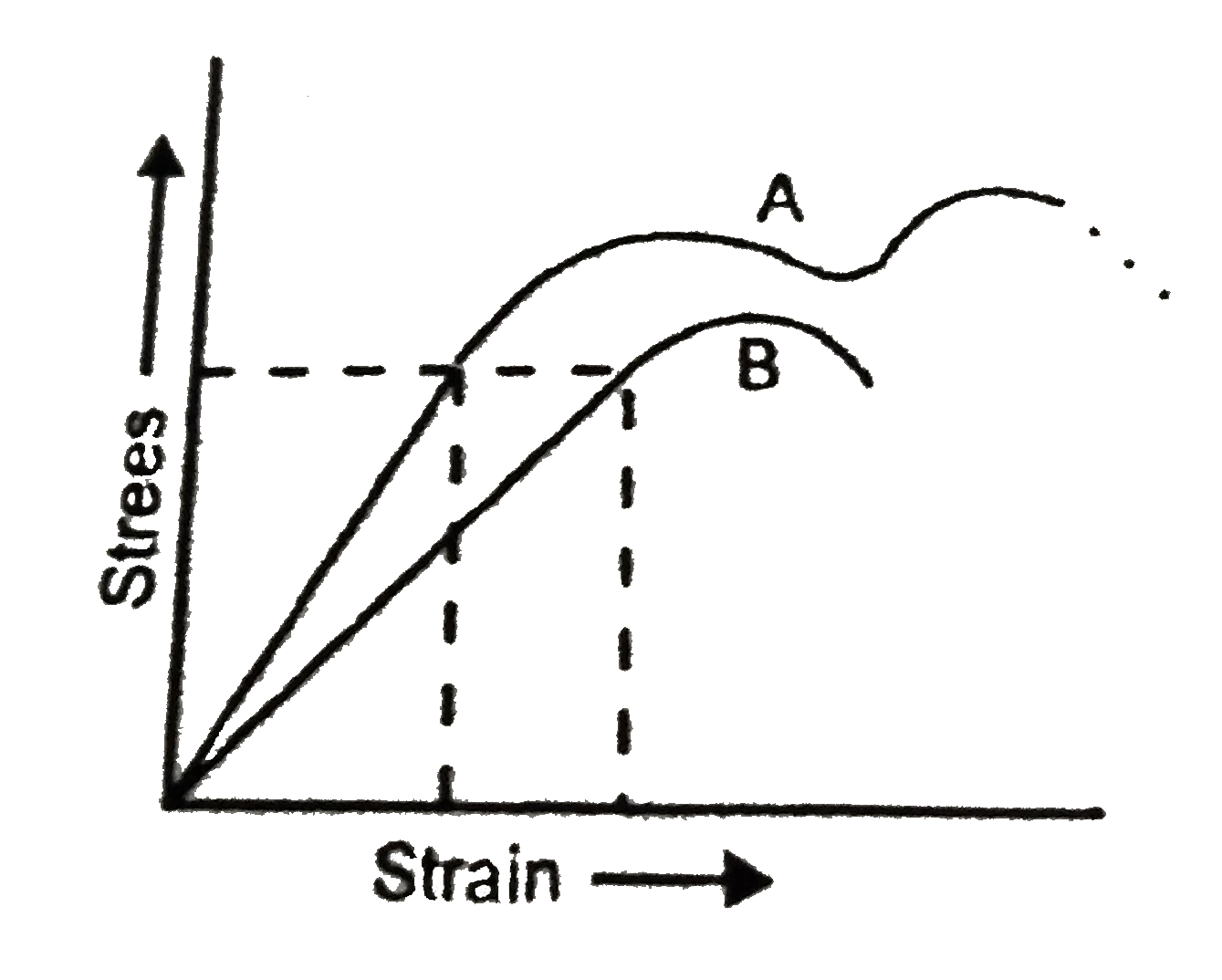
View SolutionThe stress versus strain graph for two materials A and B are shown in fig. the graph are on the same scale. ltbr> (a) Which material has greater Young's modulus?
(b) which of the two is stronger material?
View SolutionA ring of radius 0.1m is made out of thin metallic wire of area of cross section 10−6m2. The ring has a uniform charge of π coulombs. Find the change in the radius of the rig when a charge of 10−8C is placed at the center of the ring. Young's modulus of the metal is 2×1011Nm−2.
View SolutionWhich one the following is not a unit of Young's modulus ?
View SolutionAssertion The materials having low value of Young's modulus of elasticity are more ductile.
Reason If Young's modulus is less, they can be easily stretched as wires.
View Solution
