If the load of a wire is increases such that its stress is twice as that of previous, then the new value of Youngs modulus is
Increases
Remain same
Decreases
May increases or decreases
The correct Answer is:B
To solve the problem, we need to understand the relationship between stress, strain, and Young's modulus.
1. Understanding Young's Modulus:
Young's modulus (E) is defined as the ratio of stress (σ) to strain (ε):
E=σϵ
where stress (σ) is the force (F) applied per unit area (A), and strain (ε) is the change in length (ΔL) divided by the original length (L).
2. Initial Conditions:
Let the initial stress be σ₁ and the corresponding strain be ε₁. Therefore, we can write:
E=σ1ϵ1
3. New Conditions:
According to the problem, the new stress (σ₂) is twice the initial stress:
σ2=2σ1
4. Effect on Strain:
If the stress is doubled, we need to consider how strain changes. In many materials, especially those that follow Hooke's law (which is applicable for small deformations), strain is directly proportional to stress. Therefore, if stress is doubled, strain will also double:
ϵ2=2ϵ1
5. Calculating New Young's Modulus:
Now, we can calculate the new Young's modulus (E₂) using the new stress and strain:
E2=σ2ϵ2=2σ12ϵ1=σ1ϵ1=E
6. Conclusion:
The new value of Young's modulus remains the same as the original value:
E2=E
Final Answer:
The new value of Young's modulus is the same as the previous value.
Young's modulus (E) is defined as the ratio of stress (σ) to strain (ε):
E=σϵ
where stress (σ) is the force (F) applied per unit area (A), and strain (ε) is the change in length (ΔL) divided by the original length (L).
Let the initial stress be σ₁ and the corresponding strain be ε₁. Therefore, we can write:
E=σ1ϵ1
According to the problem, the new stress (σ₂) is twice the initial stress:
σ2=2σ1
If the stress is doubled, we need to consider how strain changes. In many materials, especially those that follow Hooke's law (which is applicable for small deformations), strain is directly proportional to stress. Therefore, if stress is doubled, strain will also double:
ϵ2=2ϵ1
Now, we can calculate the new Young's modulus (E₂) using the new stress and strain:
E2=σ2ϵ2=2σ12ϵ1=σ1ϵ1=E
The new value of Young's modulus remains the same as the original value:
E2=E
The new value of Young's modulus is the same as the previous value.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl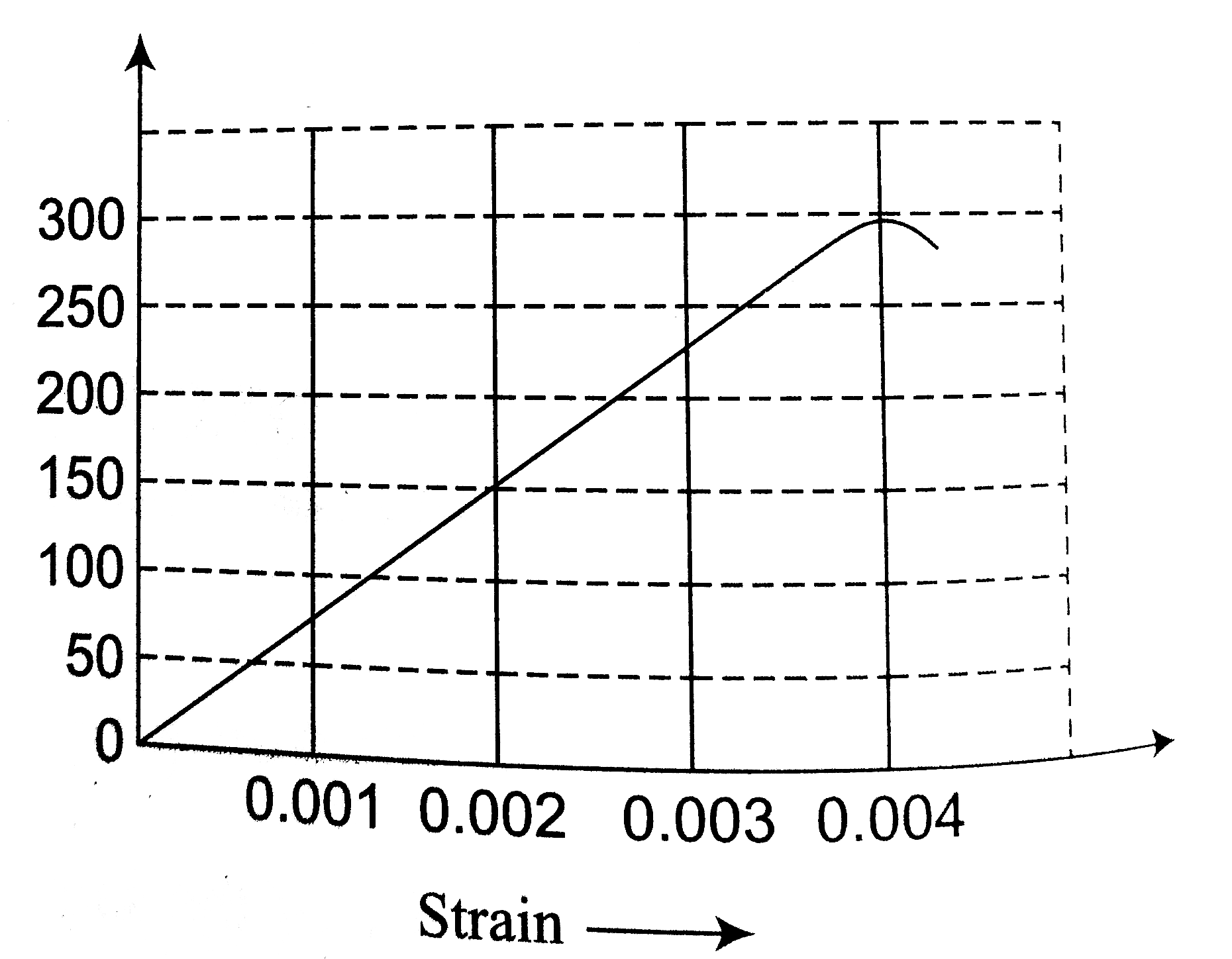
Figure shows the strain stress curve for a given material. The Young's modulus of the material isA5×109Nm−2B5×1010Nm−2C7.5×109Nm−2D7.5×1010Nm−2
With a rise of temperature, the Young’s modulus :
View SolutionA load of 4kg is suspended from a ceiling through a steel wire of length 20m and radius 2mm. It is found that the length of the wire increases by 0.031mm, as equilibrium is achieved. If g=3.1×πms(−2), the value of young's modulus of the material of the wire (in Nm−2) is
View SolutionA load of 4 kg is suspended from a ceiling through a steel wire of length 2 m and radius 2 mm. It is found that the length of the wire increase by 0.032 mm as equilibrium is achieved. What would be the Young's modulus of steel ? (Take , g=3.1πms−2)
View SolutionA steel wire is stretched by 1kgwt. If the radius of the wire is doubled, its Young's modulus will
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionWhen 1m long metallic wire is stressed, an extension of 0.02m is produced. An organ pipe 0.5m long and open at both ends, when sounded with this stressed metallic wire, produced 8 beats in its fundamental mode. By decreasing the stress in the wire, the number of beats are found to decrease. Find the Young's modulus of the wire. The density of metallic wire is 104kg/m3 and velocity of sound in air is 292m/s.
View Solution
