_E01_111_Q01.png)
Water coming out of the mouth of a tap and falling vertically in stream line flwo forms a tapering column. i.e., the area of cross-section of the liquid column decreases as it moves down which of the following is the most accurate explanantion for this-
As the moves down, its speed increases and hence its pressure decreases. It is then compressed by the atmosphere.
Falling water tries to to reach a terminal velocity and hence reduced the area of cross-section to balance upward and downward force.
The mass of water flowing past and cross-section must remain constant. Also, water is almost incompressible. Hence the rate of volume flow must remain constant. As this is equal to velocity x area, the area decreases as velocity increases.
The surface tension causes the exposed surface area of the liquid to decrease continuously.
The correct Answer is:C
Step by step video & image solution for Water coming out of the mouth of a tap and falling vertically in stream line flwo forms a tapering column. i.e., the area of cross-section of the liquid column decreases as it moves down which of the following is the most accurate explanantion for this- by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)
32 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Comprehension based questions)
24 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A cylindrical container of cross-section area, A is filled up with water upto height 'h' Water may exit through a tap of cross sectional area 'a' in the bottom of container. Find out

(a) Velocity of water just after opening of tap.
(b) The area of cross-section of water stream coming out of tape at depth h0 below tap in terms of 'a' just after opening of tap.
(c) Time in which conainer becomes empty.
(Given : (aA)1/2=0.22,h=20cm,h0=20cm
View SolutionTwo very large open tanks A&F both contain the same liquid. A horizontal pipe BCD, having a small constriction at C, leads out of the bottom of tank A, and a vertical pipe E containing air opens into the constriction at C and dips into the liquid in tank F. Assume stremline flow and no viscosity. If the cross section area at C is one-half that at D, and if D is at distance h1 below the level of the liquid in A, to what height h2 will liquid rise in pipe E? Express your answer in terms of h1.
[Neglect changes in atmosphere pressure with elevation. In the containers there is atmosphere above the water surface and D is also open to atmosphere.]

View SolutionA conical section of a pipe is shown in figure through which water is flowing. Let A be the area of crosss-section, r be the radius of cross-section, P be the pressure at a point difference and v be the velocity of water.

Match the column-I with column-II containing values of ratio of quantities given in Column-I
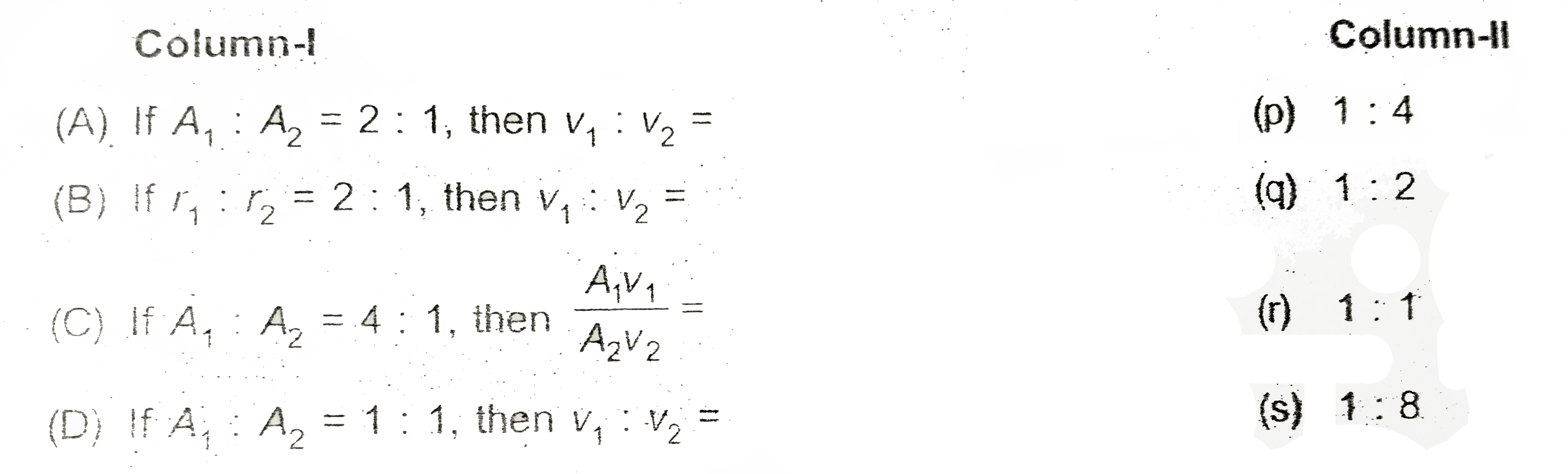
View SolutionA person in a lift is holding a water jar, which has a small hole at the lower end its side. When the lift is at rest, the water jet coming out of the hole hits the floor of the lift at a distance d of 1.2 m from the person. In the following, state of the lift’s motion is given in Column I and the distance where the water jet hits the floor of the lift is given in Column II. Match the statements from list I with those in list II and select the correct answer using the code given below the lists.

View Solution_E01_229_Q01.png)
A cylinderical tank having cross sectional area ∧=0.5m2 is filled liquids of densities ρ1=900kgm3&ρ2=600kgm3 to a height h=60cm as shown in the figure a small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom calculate.
(i). velocity of efflux
(ii). horizontal force F to keep the cylinder in static equilibrium if it is placed on a smooth horizontal plane
(iii). minimum and maximum value of F to keep the cylinder at rest. The coefficient of friction between cylinder and the plane is μ=0.1
(iv). velocity of the top most layer of the liquid column and also the velocity of the boundary separating the two liquids.
View SolutionIf a body moves through a liquid or a gas then the fluid applies a force on the body which is called drag force. Direction of the drag force is always opposite to the motion of the body relative to the fluid. At low speeds of the body, drag frog (FP) is directly proportional to the speed.
FD=kv
What K is a proportionally constant and it depends upon the dimension of the body moving in air at relatively high speeds, the drag force applied by air an the body is proportional to v2
Where this proportionally constant K can be given by
K2ρCA
Where ρ is the density of air
C is another constant givig the drag property of air
A is area of cross-section of the body
Consider a case an object of mass m is released from a height h and it falls under gravity. As it's speed increases the drag force starts increasing on the object. Due to this at some instant, the object attains equilibrium. The speed attained by the body at this instant is called "terminal speed" of the body.
Assume that the drag force applied by air on the body follows the relation FD=kv,neglect the force by buoyancy applied by air on the body then answer the following questions.
What is the pattern of acceleration change of the body ?
View SolutionIf a body moves through a liquid or a gas then the fluid applies a force on the body which is called drag force. Direction of the drag force is always opposite to the motion of the body relative to the fluid. At low speeds of the body, drag frog (FP) is directly proportional to the speed.
FD=kv
What K is a proportionally constant and it depends upon the dimension of the body moving in air at relatively high speeds, the drag force applied by air an the body is proportional to v2
Where this proportionally constant K can be given by
K2ρCA
Where ρ is the density of air
C is another constant givig the drag property of air
A is area of cross-section of the body
Consider a case an object of mass m is released from a height h and it falls under gravity. As it's speed increases the drag force starts increasing on the object. Due to this at some instant, the object attains equilibrium. The speed attained by the body at this instant is called "terminal speed" of the body.
Assume that the drag force applied by air on the body follows the relation FD=kv,neglect the force by buoyancy applied by air on the body then answer the following questions.
What is the terminal speed of the object ?
View SolutionA block is released on the slant face of a wedge of equal mass placed on a horizontal floor. The slant face of the wedge makes an angle of 45∘ with the floor. Coefficient of friction between all surfaces in contact is the same. Different value/ range of coefficient of friction is given in column I and corresponding consequences in column II and III (wedge is fress to move)

Column-IColumn-IIColumn-III(I)μ=0(i)Work done by friction on block and wedge is negative (on each)(P)Centre of mass of system (block+wedge) moves rightward and downward(II)μ>1(ii)Work done by friction on block is negative but on wedge it is zero(Q)Centre of mass of system (block+wedge) moves leftward and downward(III)√5−2<μ<1(iii)Work done by friction on block and wedge is zero (on each)(R)Centre of mass of system (block+wedge) remains at rest(IV)μ<√5−2(iv)Friction between the block and wedge is static and between the wedge and ground it is kinetic in nature.(S)Centre of mass of system (block+wedge) moves vertically downward
Which of the following options is the correct representaion of the case that the block slides down the wedge and wedge slide on the floor
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A constant potential difference is maintained between the ends of a conductor having nonuniform cross-section. Which of the following quantities will not change along the length of the conductor
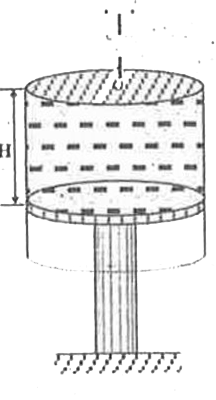
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is
View Solution
