A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
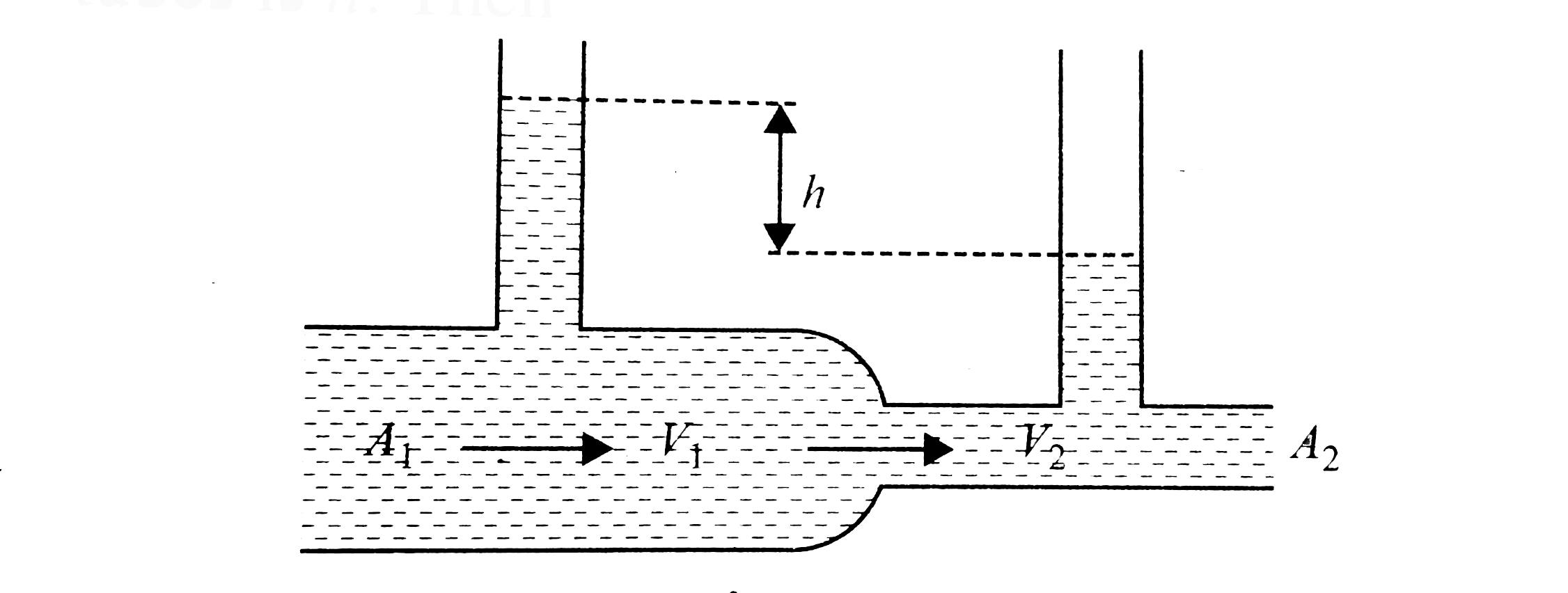
The volume of the liquid flowing through the tube in unit time is A1v1
v2−v1=√2gh
v22−v21=2gh
The energy per unit mass of the liquid is the same in both sections of the tube.
The correct Answer is:A, C, D
Step by step video & image solution for A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A_(1) and A_(2) are v_(1) and v_(2) respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)
32 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Comprehension based questions)
24 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
An incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:

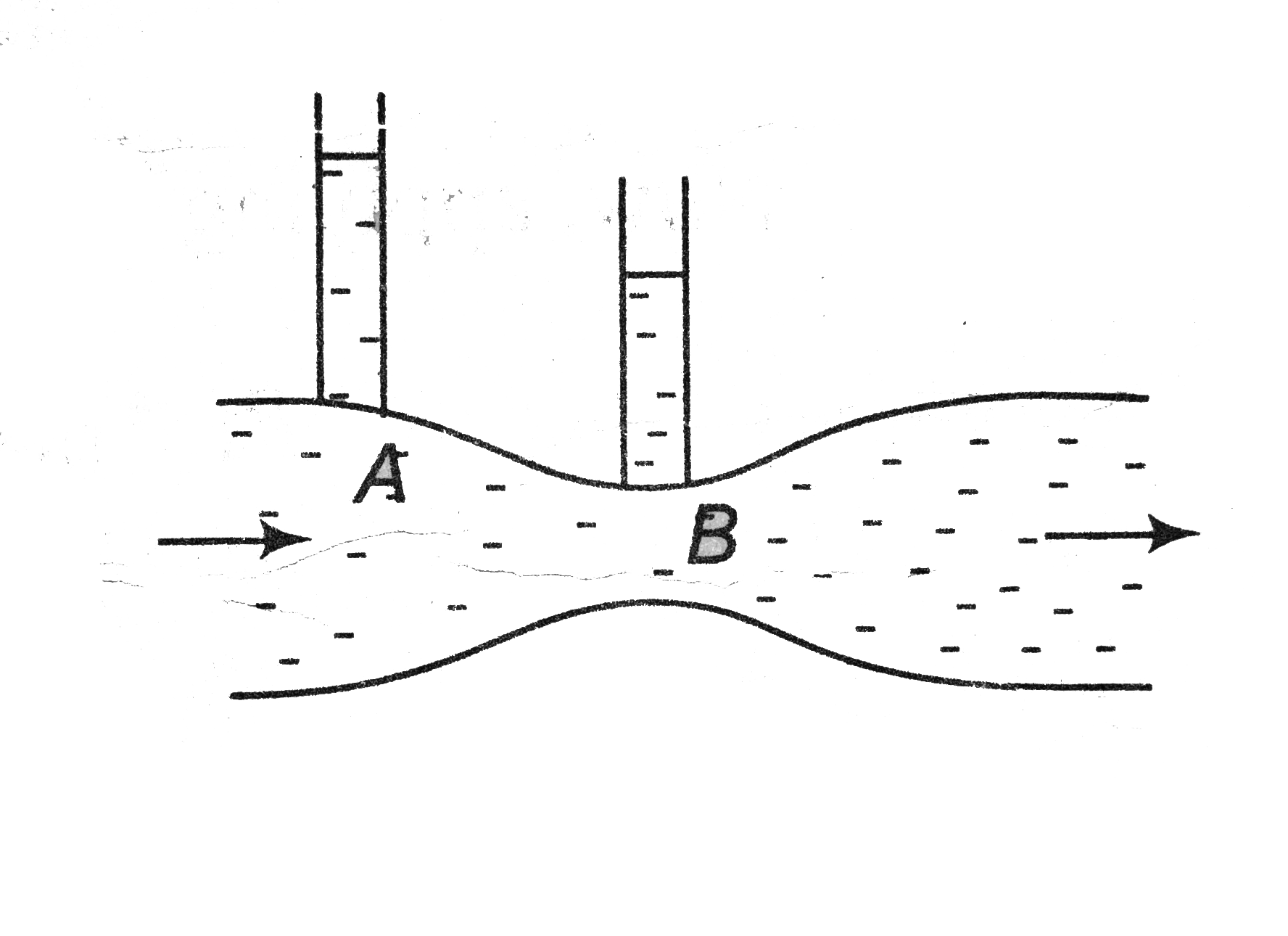
View SolutionWater flows through a horizontal tube as shown in figure. If the difference of heights of water colun in the vertical tubes is 2 cm and the area of cross section at A and B are 4cm2and2cm2 respectively, find the rate of flow of water across any section.

View Solution
Knowledge Check
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Water flows through a horizontal tube as shown in figure. If the difference of height of water column in the vertical tubes in 2cm and the areas of corss-section at A and B are 4cm2 and 2cm2 respectively. Find the rate of flow of water across any section.
 .
.
View SolutionWater flows through a horizontal tube of variable cross-section. The area of cross section at A and B are 4mm2and2mm2 respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference PA−PB.

View SolutionWater flows through a horizontal tube of variable cross section.The area of cross section at A and B are 4 mm2and2mm2 respectively. If 1 cc of water enters per second through A find
a) The speed of water at A
b) the speed of river at B
c) the pressure difference PA−PB.

View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :
View SolutionIn a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -
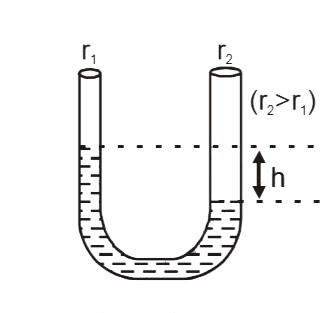
View SolutionA horizontal tube has different cross sections at points A and B. The areas of cross section are a1 and a2 respectively, and pressures at these points are p1=ρgh1 and p2=ρgh2 where ρ is the density of liquid flowing in the tube and h1 and h2 are heights of liquid columns in vertical tubes connected at A and B. If h1−h2=h, then the flow rate of the liquid in the horizontal tube is
View SolutionA pipe of non uniform cross section has two distinct section 1 and 2 with areas 2cm2 and 4cm2 respectively. If the velocity of flowing liquid at section 1 is 5cm/s, determine the velocity at section 2.
View Solution
