A vertical U−tube contains a liquid. The total length of the liquid column inside the tube is 1. When the liquid is in equilibrium, the liquid surface in one of the arms of the U−tube is pushed down slightly and released. The entire liquid column will undergo a periodic motion.
The motion is not simple harmonic motion.
the motion is simple harmonic motion
if it undergoes simple harmonic motion the time period will be 2π√lg
It is undergoes simple harmonic motion the time period will be 2π√l2g
The correct Answer is:B, D
To solve the problem, we need to analyze the motion of the liquid in the U-tube when it is disturbed slightly from its equilibrium position. Here’s a step-by-step solution:
Step 1: Understanding the Setup
We have a U-tube filled with a liquid of density ρ and total length L. Initially, the liquid levels in both arms of the U-tube are equal. When one side is pushed down by a small distance y, the liquid in the other arm rises by the same distance y.
Hint: Visualize the U-tube and the liquid levels before and after the disturbance.
Step 2: Determine the Mass of the Liquid Column
The mass of the liquid in the U-tube can be calculated using the formula:
mi=ρ⋅V=ρ⋅A⋅L
where A is the cross-sectional area of the tube.
Hint: Remember that the volume of the liquid is the product of the cross-sectional area and the height of the liquid column.
Step 3: Analyzing the Displacement
When the liquid is pushed down by y in one arm, the height of the liquid in that arm becomes L+y, while the height in the other arm becomes L−y. The effective height of the liquid column that contributes to the restoring force is 2y.
Hint: Consider how the liquid levels change in both arms when one side is pushed down.
Step 4: Calculating the Restoring Force
The restoring force F acting on the liquid column due to the weight of the displaced liquid can be expressed as:
F=−Weight of the liquid column=−ρ⋅A⋅(2y)⋅g
This can be simplified to:
F=−2ρAgy
Hint: The negative sign indicates that the force acts in the opposite direction to the displacement.
Step 5: Relating Restoring Force to Simple Harmonic Motion
According to Hooke's law, the restoring force is proportional to the displacement:
F=−ky
where k is the spring constant. From our expression for F:
k=2ρAg
Hint: Recognize that the form of the restoring force indicates that the motion is simple harmonic.
Step 6: Finding the Time Period
The time period T of simple harmonic motion is given by:
T=2π√mk
Substituting m=ρAL and k=2ρAg:
T=2π√ρAL2ρAg=2π√L2g
Hint: Simplify the expression by canceling out common terms.
Final Result
The time period of the oscillation of the liquid column in the U-tube is:
T=2π√L2g
Summary
The liquid in the U-tube undergoes simple harmonic motion when disturbed, and the time period of this motion is T=2π√L2g.
---
We have a U-tube filled with a liquid of density ρ and total length L. Initially, the liquid levels in both arms of the U-tube are equal. When one side is pushed down by a small distance y, the liquid in the other arm rises by the same distance y.
The mass of the liquid in the U-tube can be calculated using the formula:
mi=ρ⋅V=ρ⋅A⋅L
where A is the cross-sectional area of the tube.
When the liquid is pushed down by y in one arm, the height of the liquid in that arm becomes L+y, while the height in the other arm becomes L−y. The effective height of the liquid column that contributes to the restoring force is 2y.
The restoring force F acting on the liquid column due to the weight of the displaced liquid can be expressed as:
F=−Weight of the liquid column=−ρ⋅A⋅(2y)⋅g
This can be simplified to:
F=−2ρAgy
According to Hooke's law, the restoring force is proportional to the displacement:
F=−ky
where k is the spring constant. From our expression for F:
k=2ρAg
The time period T of simple harmonic motion is given by:
T=2π√mk
Substituting m=ρAL and k=2ρAg:
T=2π√ρAL2ρAg=2π√L2g
The time period of the oscillation of the liquid column in the U-tube is:
T=2π√L2g
The liquid in the U-tube undergoes simple harmonic motion when disturbed, and the time period of this motion is T=2π√L2g.
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)
32 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Comprehension based questions)
24 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
Motion of an oscillating liquid column in a U-tube is
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.

View Solution
Knowledge Check
Motion of an oscillating liquid column in a U-tube is
Aperiodic but not simple harmonic.Bnon-periodicCsimple harmonic and time period is independent of the density of the liquid.Dsimple harmonic and time period is directly proportional to the density of the liquid.Motion of an oscillating liquid column in a U-tube is
Aperiodic but not simple harmonic.Bnon-periodicCsimple harmonic and time period is independent of the density of the liquid.Dsimple harmonic and time period is directly proportional to the density of the liquid.When a capillary tube is dipped in a liquid, the liquid rises to a height H in the tube. The free liquid surface inside the tube is hemispherical in shape. The tube is now pushed down sothat the height of the tube outside the liquid is less than H. Then the
Aliquid will come out of the tube like in a small fountainBliquid will ooze out of the tube slowlyCfree liquid surface inside the tube is hemisphericalDthe liquid will fill the tube but not come out its upper end.
An ideal liquid having length of liquid column l is column in V-shape take as shown. If liquid is displaced, then its time period is
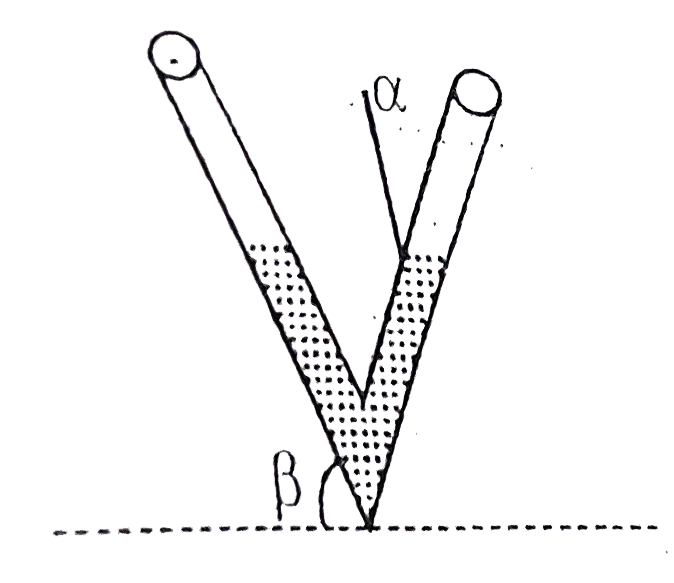
View SolutionA U-tube contains a liquid to a height of 9.8 cm in one of the limbs. The tube is vertical. If the liquid on one side is depressed a little and released its motion in the tube is simple harmonic motion. Find its period.
View SolutionFind time period of liquid column of length l in the shown tube.

View SolutionA vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
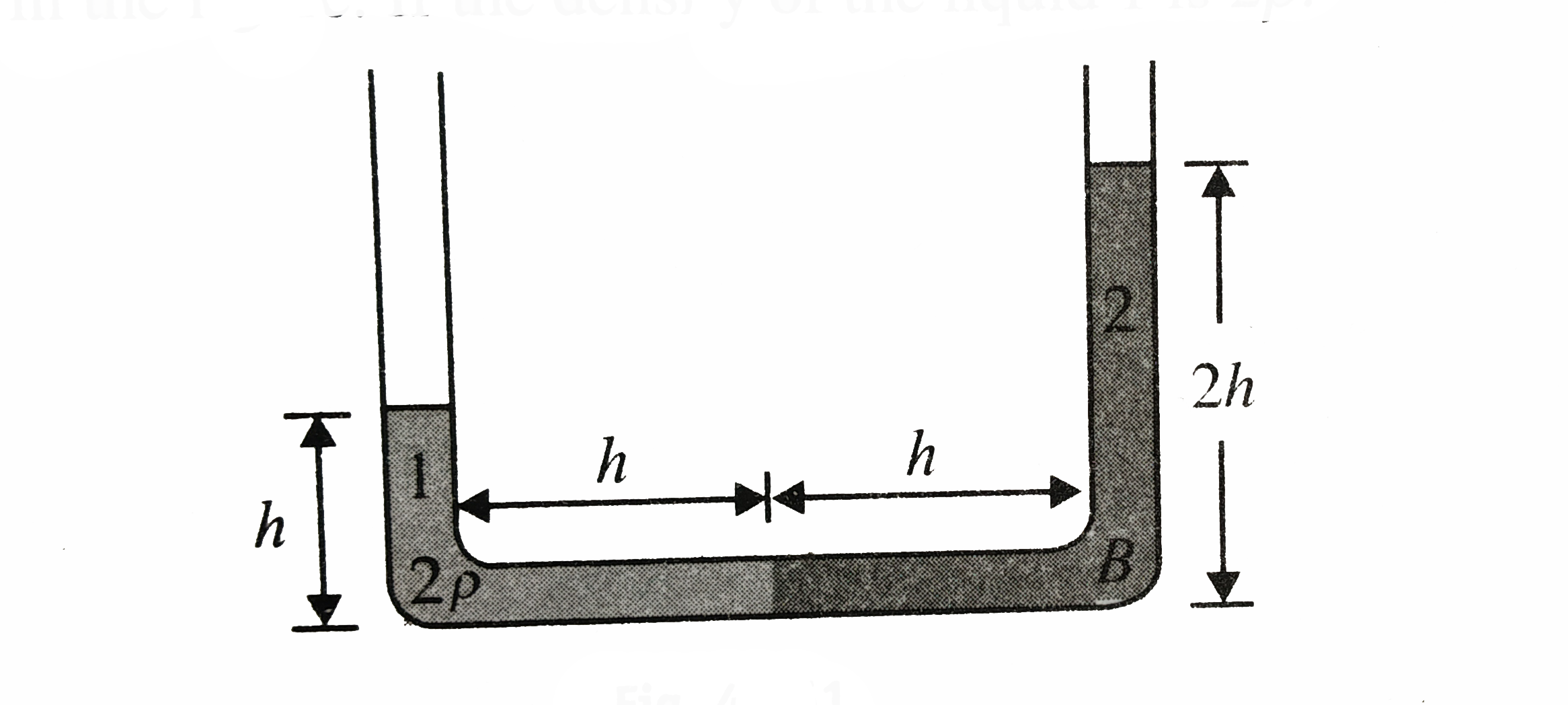
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.
View SolutionMotion of a liquid in a tube is describe by
View Solution
