A bottle has an opening of radius a and length b. A cork of length b and radius (a+ΔA) is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is then the force needed to push the cork into the bottle is :
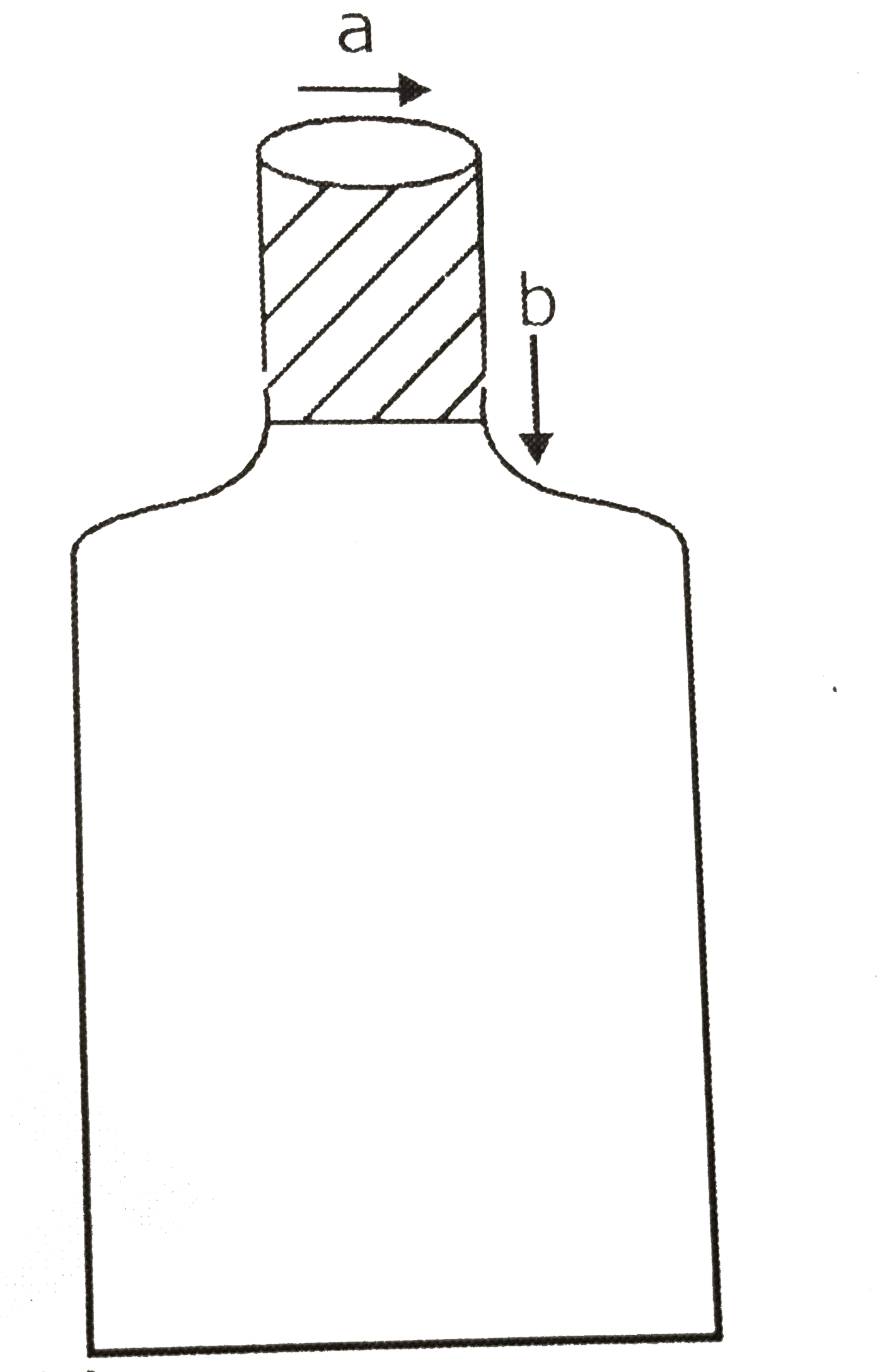
(2πμBb)Δa
(πμBb)Δa
(4πμBb)Δa
(πμBb)a
The correct Answer is:C
Step by step video & image solution for A bottle has an opening of radius a and length b. A cork of length b and radius (a+Delta A) is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is then the force needed to push the cork into the bottle is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (MCQ)13videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Multiple correct answers)2videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 B (Bran storming Subjective Exercise)15videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
Similar Questions
The neck and bottom of a bottle are 3 cm and 15 cm in radius respectively. If the cork is pressed with a force 12 N in the neck of the bottle, then force exerted on the bottom of the bottle is :-
View SolutionA man of mass m walks from end A to the other end B of a boat of mass M and length l. The coefficient of friction between the man and the boat is μ an neglect any resistive force between the boat and the water.
View Solution
Knowledge Check
- Question 1 - Select One
In a triangle with sides of lengths 3,4, and 5, the smallest angle is 37.87∘. In the figure, O is the center of the circle of radius 5. A and B are two points on the circle , and the distance between the points is 6. what is the value of x?
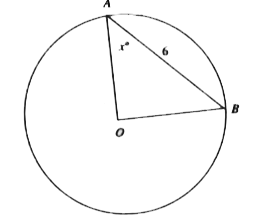 A36.87B45C53.13D116.85
A36.87B45C53.13D116.85
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road figure. A small bock of mass 100 g is kept on the seat which rests against the plate. The friction coefficient between the block and the plate is μ=0.58. a. Find the normal contact force exerted by the plate on the block. b. The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases Find the angle at which the block will just start sliding on the plate.
 View Solution
View SolutionFigure shown a small block A of mass m kept at the left end of a plank B of mass M=2m and length l . The system can slide on a horizontal road. The system is started towards right with the initial velocity v. The friction coefficient between the road and the plank is 1/2 and that between the plank and the block is 1/4 . Find

(a) the time elapsed before the block separates from the plank
(b) displacement of block and plank relative to ground till that moment.View SolutionTwo blocks A and B of mass m and 2m are intially at rest. Length of block B is L and the block A is placed at the right end corner of block B and the friction coefficient between them is μ=1/2. At t=0 a constant force F =5mg2 begins to act on block B towards right. just when the block A leaves B, wind begins to below along y-direction which exerts a constant force mg2 on A. assume that size block A is small compared to B and neglect any rotational effects and toppling of block B. (given h=1/2m, L=1 m and g=10m/s2)
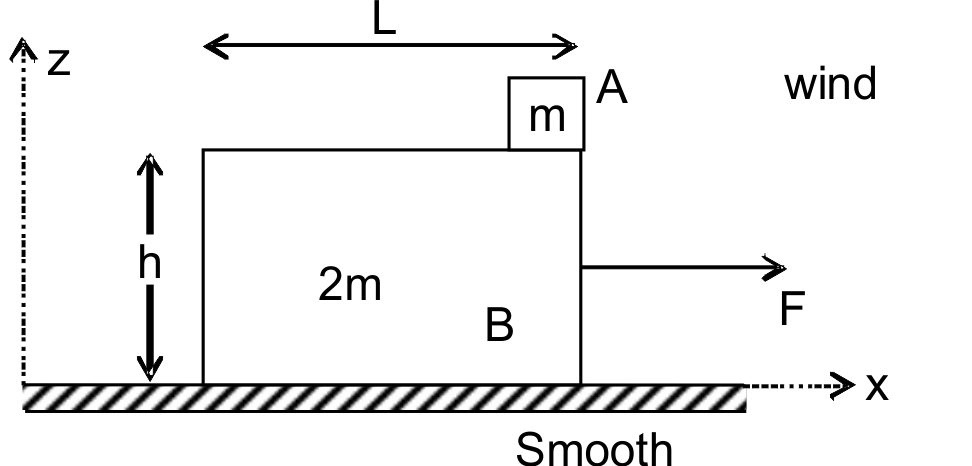
The magnitude of relative acceleration of A with respect to B ( in m/s2) just after the block A leaves B is (assume wind does not effects motion of B)View SolutionA block is mass m moves on as horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v write a. the normal force by the wall on the block. b. the frictional force by the wall and c. the tangential acceleration of the block. d. Integrate the tangential acceleration (dvdt=vdvds) to obtain the speed of the block after one revoluton.
View SolutionA track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2
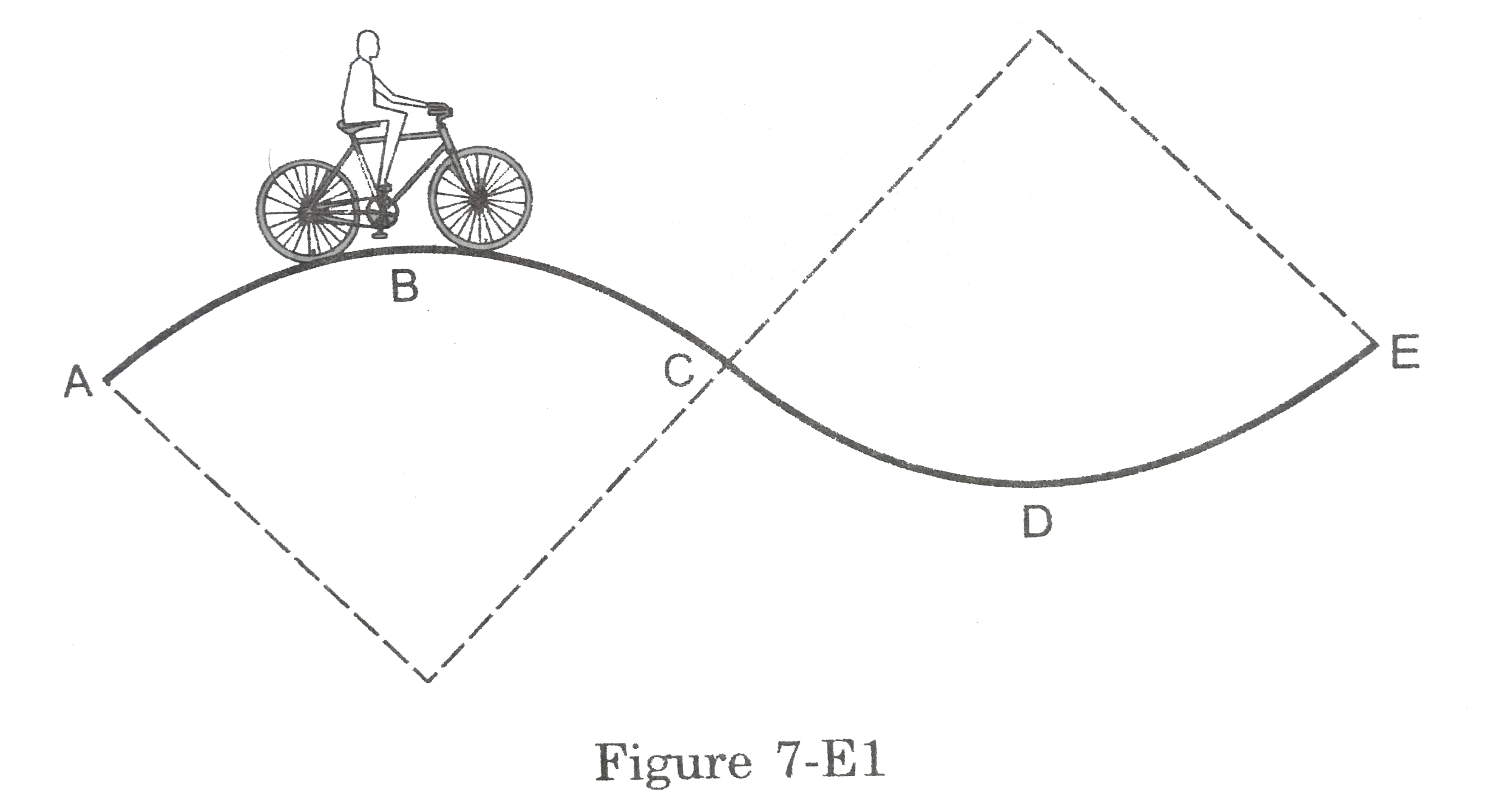 View Solution
View SolutionA block of mass 5kg is (i) pushed in case (A) and (ii) pulled in case (B), by a force F=20N, making an angle of 30∘ with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is μ=0.2. The difference between the accelerattion of the block, in case (B) and case (A) will be : (g=10ms−2).
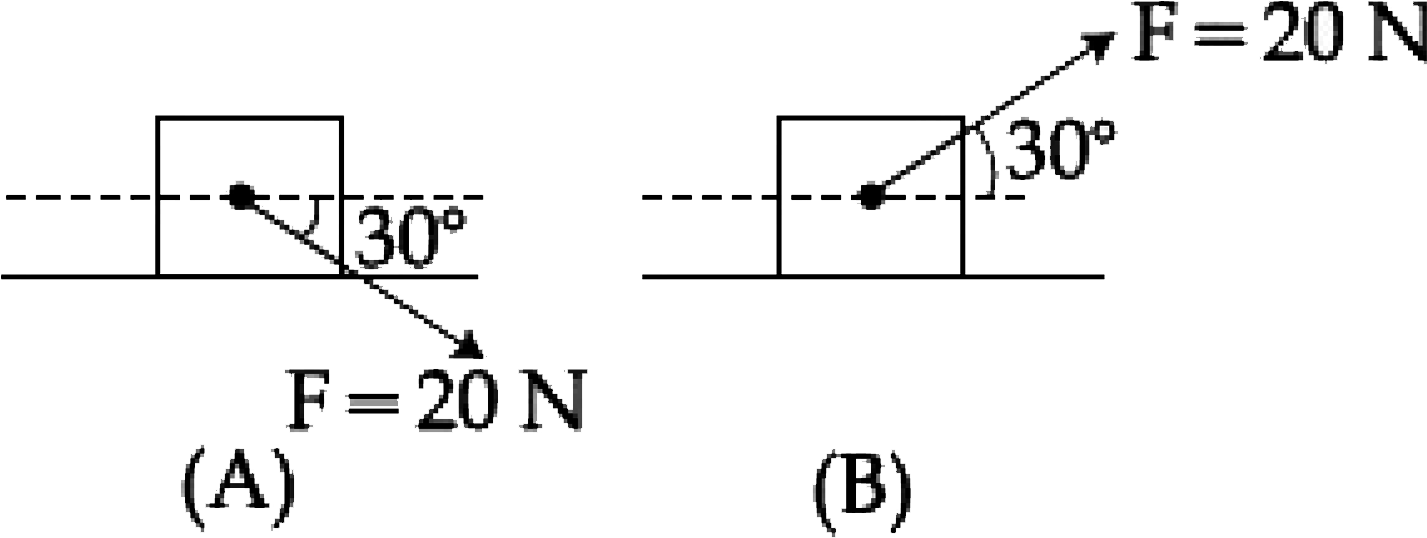 .View Solution
.View Solution
Charge 'q' is uniformly distributed along the length of a non-coducting circular ring of mass m and radius 'a'. The ring is placed concentrically magnetic field B=kt (where k is constant) is existing perpendicular to the plane of circular region of radius 'R' as shown. The minimum coefficient of friction between the ring and the surface required to keep the ring stationary isView Solution

