A satellite is in a circular orbit very close to the surface of a planet. At some point it is given an impulse along its direction of motion, causing its velocity to increase n times . It now goes into an elliptical orbit. The maximum possible value of n for this to occur is
2
√2
√2+1
1√2−1
The correct Answer is:B
To solve the problem, we need to determine the maximum value of n such that a satellite, initially in a circular orbit, can still remain in an elliptical orbit after its velocity is increased n times.
1. Determine the Initial Velocity of the Satellite:
The initial velocity Vi of a satellite in a circular orbit very close to the surface of a planet is given by:
Vi=√GMR
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
2. Determine the Escape Velocity:
The escape velocity Ve from the surface of the planet is given by:
Ve=√2GMR
3. Condition for Elliptical Orbit:
For the satellite to remain in an elliptical orbit after the velocity is increased n times, the new velocity Vf must be less than or equal to the escape velocity:
Vf=nVi≤Ve
4. Substituting the Expressions for Velocities:
Substituting the expressions for Vi and Ve:
n√GMR≤√2GMR
5. Simplifying the Inequality:
We can simplify this inequality by squaring both sides (since both sides are positive):
n2GMR≤2GMR
Canceling GMR from both sides (assuming GM/R≠0):
n2≤2
6. Finding the Maximum Value of n:
Taking the square root of both sides gives:
n≤√2
Therefore, the maximum possible value of n is:
n=√2
Conclusion:
The maximum possible value of n for the satellite to still remain in an elliptical orbit after the impulse is:
√2
The initial velocity Vi of a satellite in a circular orbit very close to the surface of a planet is given by:
Vi=√GMR
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
The escape velocity Ve from the surface of the planet is given by:
Ve=√2GMR
For the satellite to remain in an elliptical orbit after the velocity is increased n times, the new velocity Vf must be less than or equal to the escape velocity:
Vf=nVi≤Ve
Substituting the expressions for Vi and Ve:
n√GMR≤√2GMR
We can simplify this inequality by squaring both sides (since both sides are positive):
n2GMR≤2GMR
Canceling GMR from both sides (assuming GM/R≠0):
n2≤2
Taking the square root of both sides gives:
n≤√2
Therefore, the maximum possible value of n is:
n=√2
The maximum possible value of n for the satellite to still remain in an elliptical orbit after the impulse is:
√2
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)
20 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 4 A (Conceptual Subjective Exercise)
14 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 1 (Check your Grasp)
28 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
If a satellite is orbiting the earth very close to its surface, then the orbital velocity mainly depends on
View SolutionA satellite is revolving around earth in a circular orbit. At some instant the speed of the satellite is increased √2 times its orbital speed keeping its direction unchanged. Then, the new path of the satellite is :
View Solutionsatellite revolving in circular orbit suppose V0 is the orbital speed, T its time period, u its potential energy and K the kinetic energy. Now value of G is decreasesd. Then
View SolutionA small satellite revolves around a heavy planet in a circular orbit. At certain point in its orbit a sharp impulse acts on it and instantaneously increases its kinetic energy to 'k' (<2) times without change in its direction of motion show that in its subsequent motion the ratio of its maximum and minimum distance from the planet is k2−k assuming the mass of the satellite is negligibly small as compared to that of the planet.
View SolutionA satellite is revolving very close to the earth surface in a circular orbit has potential energy U. Find the change in its mechanical energy if it is made to move away from earth such that its velocity becomes half while going around the earth in a larger circular orbit.
View SolutionAn artificial satellite (mass m) of a planet (mass M) revolves in a circular orbit whose radius is n times the radius R of the planet in the process of motion the satellite experiences a slight resistance due to cosmic dust. Assuming the force of resistance on satellite to depend on velocity as F=av2 where 'a' is a constant caculate how long the satellite will stay in the space before it falls on to the planet's surface.
View SolutionA light satellite is initially rotating around a planet in a circular orbit of radius r. Its speed in this circular orbit was u0. It is put in an elliptical orbit by increasing its speed form u0 to vQ ( instantaneously). In the elliptical orbit, the satellite reaches the farthest point P, which is at a distance R from the planet. Satellite's speed at farthest point is vP. At point Q, the speed required by satellite to escape the planet's gravitational pull is vesc
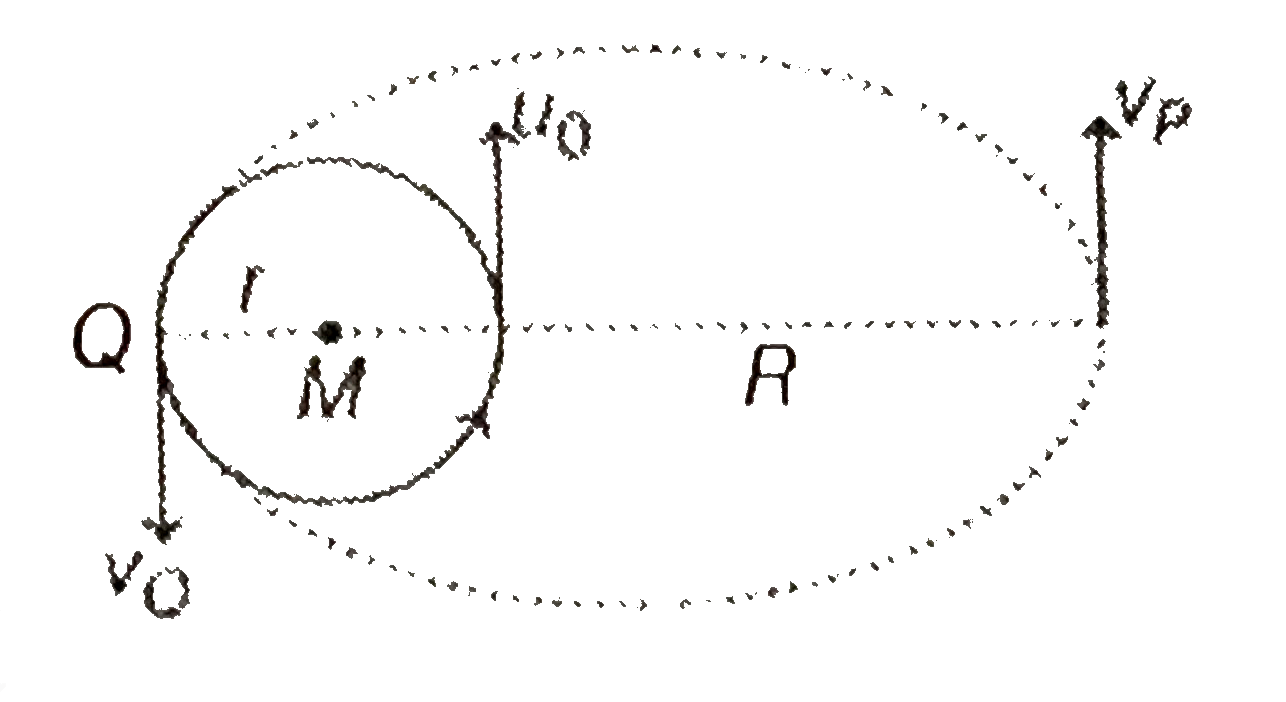
View SolutionA satellite is orbiting around the earth in a circular orbit of radius r. A particle of mass m is projected from the satellite in a forward direction with a velocity v=2/3 times the orbital velocity (this velocity is given w.r.t. earth). During subsequent motion of the particle, its minimum distance from the centre of earth is
View SolutionSTATEMENT -1 : If a body is projected from a satellite so as to escape then its velocity of projection with respect to the satellite depends upon the direction of projection.
STATEMENT -2 : Speed of a planet revolving around the sun in an elliptical orbit is maximum at perigee and minimum at apogee.
STATEMENT - 3 : Gravitational field is conservative in nature.
View SolutionA satellite is orbiting around the earth in a circular orbit and in this orbit magnitude of its acceleration is a1 . Now a rocket is fired in the direction of motion of satellite from the satellite due to which its speed instantaneously becomes half of initial, just after the rocket is fired acceleration of satellite has magnitude a2 . Then the ratio a1a2 is (Assume there is no external force other than the gravitational force of earth before and after the firing of rocket from the satellite)
View Solution
