A Young's double slit interference arrangement with slits S1 and S2, where S2 is immersed in water (refractive index =4/3). Surface of water is exactly between the two slits. The positions of maxima on the surface of water are given by x2=p2m2λ2−d2, where λ is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........

The correct Answer is:3
_E01_143_S01.png)
x1=√x2+d2
x2=43√x2+d2
Δx=(43−1)√x2+d2=nλ
13√x2+d2=nλ
(x2+d2)=9n2λ2
∴(P=3)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)7videos
WAVE OPTICS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 5 A (Previous Years Questions)17videos
WAVE OPTICS
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
A Young's double slit interference arrangement with slits S1 and S2, where S2 is immersed in water (refractive index =4/3). Surface of water is exactly between the two slits. The positions of maxima on the surface of water are given by x2=p2m2λ2−d2, where λ is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........
 View Solution
View SolutionIn Young's double slit experiment, how many maxima can be obtained on a screen (including central maxima). If d=5λ2 (where λ is the wavelength of light)?
View Solution
Knowledge Check
- Question 1 - Select One
In Young's double slit experiment, the distance d between the slits S1 and S2 is 1 mm. What should the width of each slit be so as to obtain 10 maxima of the double slit pattern within the central maximum of the single slit pattern ?
A0.9 mmB0.8 mmC0.2 mmD0.6 mm
Determine what happens to the double slits interference pattern if one of the slits is covered with a thin, transparent film whose thickness is λ2(μ−1), where λ is the wavelength of the incident light and mu is the index of refraction of the film.
View SolutionIn a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec μ is placed in front of the slit S1, then the path difference (S1P−S2P) is
 View Solution
View SolutionDraw a neat labelled diagram of Young.s Double Slit experiment. Show that β=λDd, where the terms have their usual meaning (either for bright or dark fringe).
View SolutionIf Young.s double slit apparatus is shifted from air to water, then
View SolutionIn young's double slit experiment, distance between the slit S1andS2 is d and the distance between slit and screen is D . Then longest wavelength that will be missing on the screen in front of S1 is
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionYoung's double slit experiment is conducted in a liquid of refractive index μ1 as shown in figure. A thin transparent slab of refractive index μ2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is
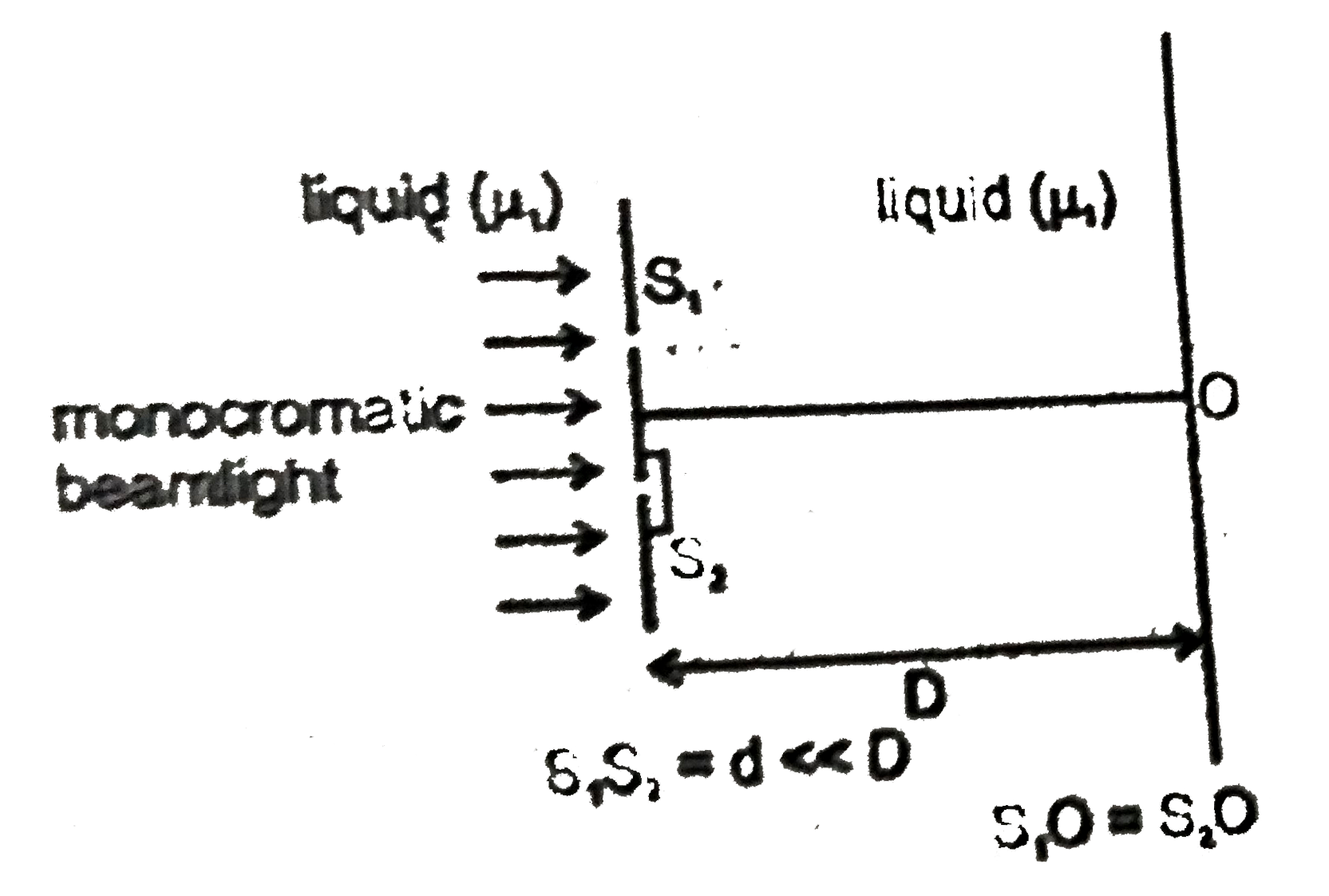 View Solution
View Solution

