A string with tension T and mass per unit length μ is clamped down at x=0 and at x=L. at t=0, the string is at rest and displaced in the y-direction
y(x,0)=2sin2πxL+2sinπxL
Q. The string is released at t=0, and it starts to oscillate. the displacement of string at time t is
The correct Answer is:A2π2T4l
l=λ2⇒λ=2l,k=2πλ=πl
The amplitude at a distance x from x = 0 is given
Total mechanical energy at x of length dx is
dE=12(dm)A2ω2=12(μdx)(asinkx)2(2πf)2
⇒dE=2π2μf2a2sin2kxdx
Here, f=v2λ2=(Tμ)(4l2)andk=πl
Substituting these values in equation (i) adn integrating it from x=0 to x=l, we get total energy of string.
E=π2a2T4l
_E01_211_S01.png)
Topper's Solved these Questions
Similar Questions
A string with tension T and mass per unit length μ is clamped down at x=0 and at x=L. at t=0, the string is at rest and displaced in the y-direction
y(x,0)=2sin2πxL+3sinπxL
Q. What is the total energy at t=0?
View SolutionA standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
View Solution
Knowledge Check
The transverse displacement of a string clamped at its both ends is given by
y(x,t)=2sin(2π3x)cos(100πt)
where x and y are in cm and t is in s.
Which of the following statements is correct?AAll the points on the string between two consecutive nodes vibrate with same frequency, phase and amplitude.BAll the points on the string between two consecutive nodes vibrate with same frequency and phase but different amplitude.CAll the points on the string between two consecutive nodes vibrate with different frequency and phase but same amplitude.DAll the points on the string between two consecutive nodes vibrate with different frequency, phase and amplitude
A string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).

View SolutionThe equation of a standing wave produced on a string fixed at both ends is y=0.4sinπx10cos600πt where y' is measured in om 10 What could be the smallest length of string?
View SolutionThe displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given by f(t)=Asin(tT). The wave speed is v. Write the wave equation.
View SolutionThe displacement of a string is given by y(x,t)=0.06sin(2πx/3)cos(120πt) where x and y are in m and t in s. The lengthe of the string is 1.5m and its mass is 3.0×10−2kg.
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given by
View SolutionThe wave-function for a certain standing wave on a string fixed at both ends is y(x,t)=0.5sin(0.025πx)cos500t where x and y are in centimeters and t is seconds. The shortest possible length of the string is :
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
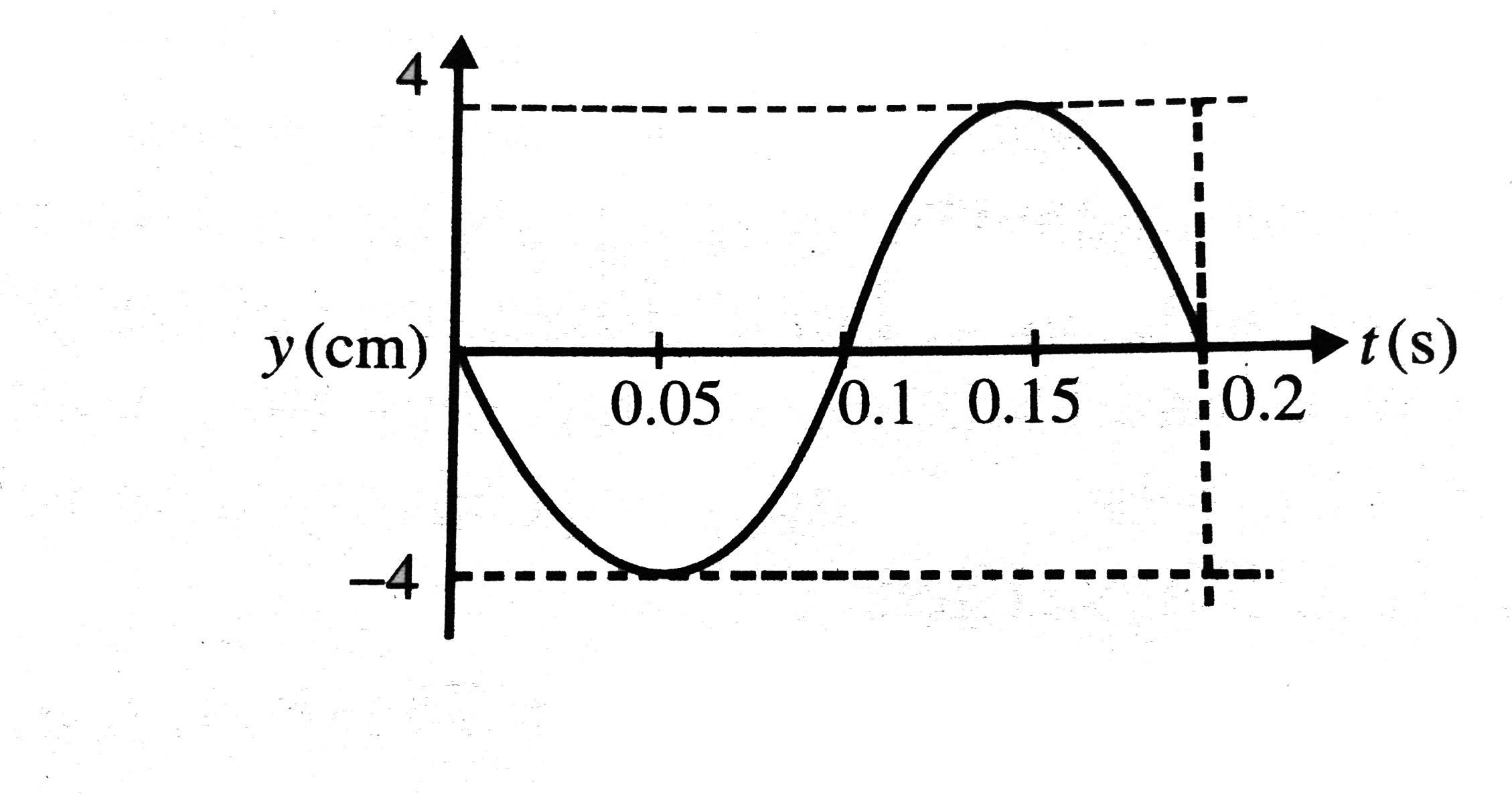
View Solution
