In the following figure, a sphere of radius 3m rolls on a plank. The accelerations of the sphere and the plank. The accelerations of the sphere and the plank are indicated. The value of α is

3rad/s2
6rad/s2
3rad/s2 (opposite to the direction shown in figure)
1rad/s2
The correct Answer is:A
α1=Rα−α2⇒3=α×3−6⇒α=3rad/s2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 260videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 399videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS44videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
A sphere rolls down on an inclied plane of inclination θ. What is the acceleration as the sphere reaches bottom ?
View SolutionA sphere rolls down on an inclined plane of inclination θ. What is the acceleration as the sphere reaches bottom?
View SolutionA sphere of mass m rolls without slipping on an inclined plane of inclination θ. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
View SolutionA man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
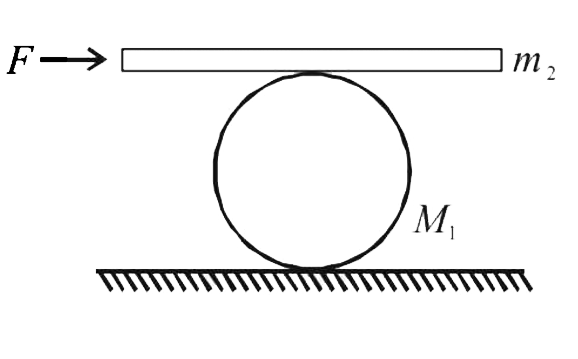
(b) the magnitudes and direction of frictional force at contact points.View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
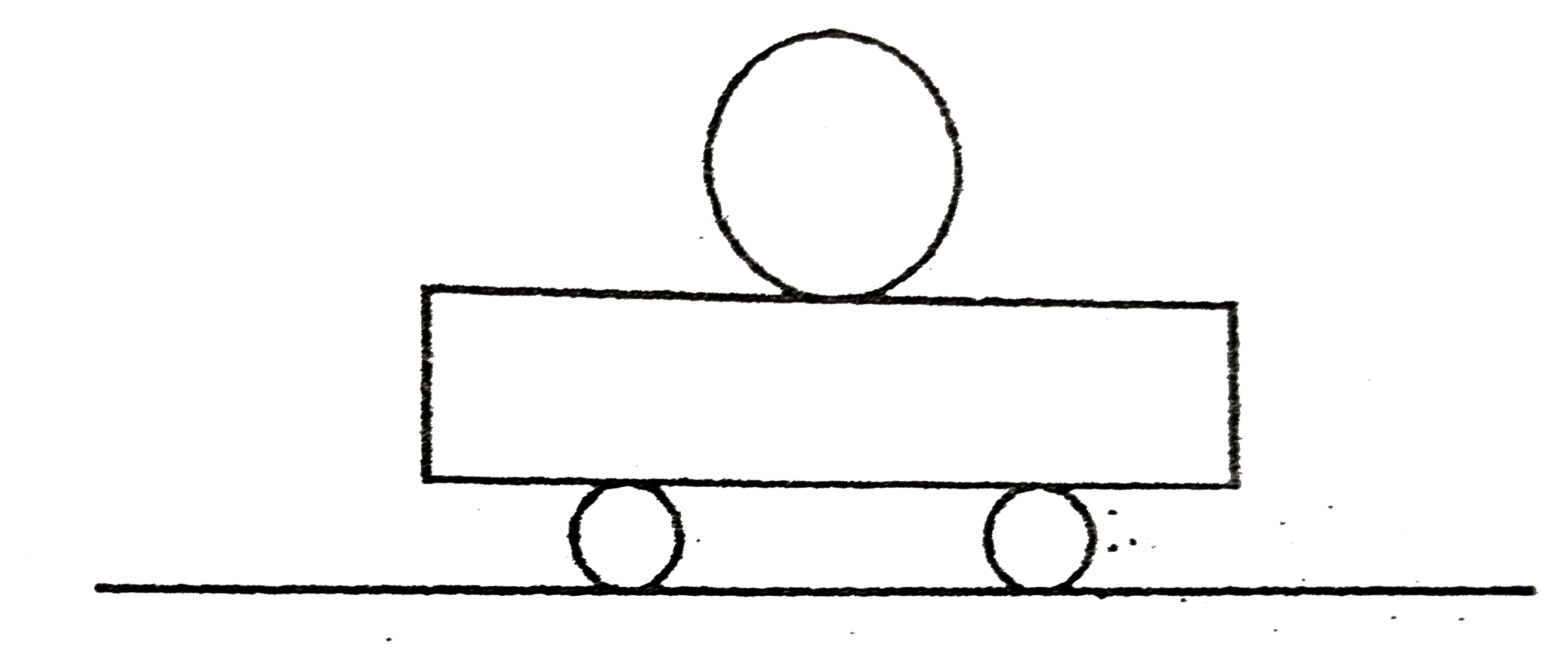
Angular acceleration of sphere isView SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
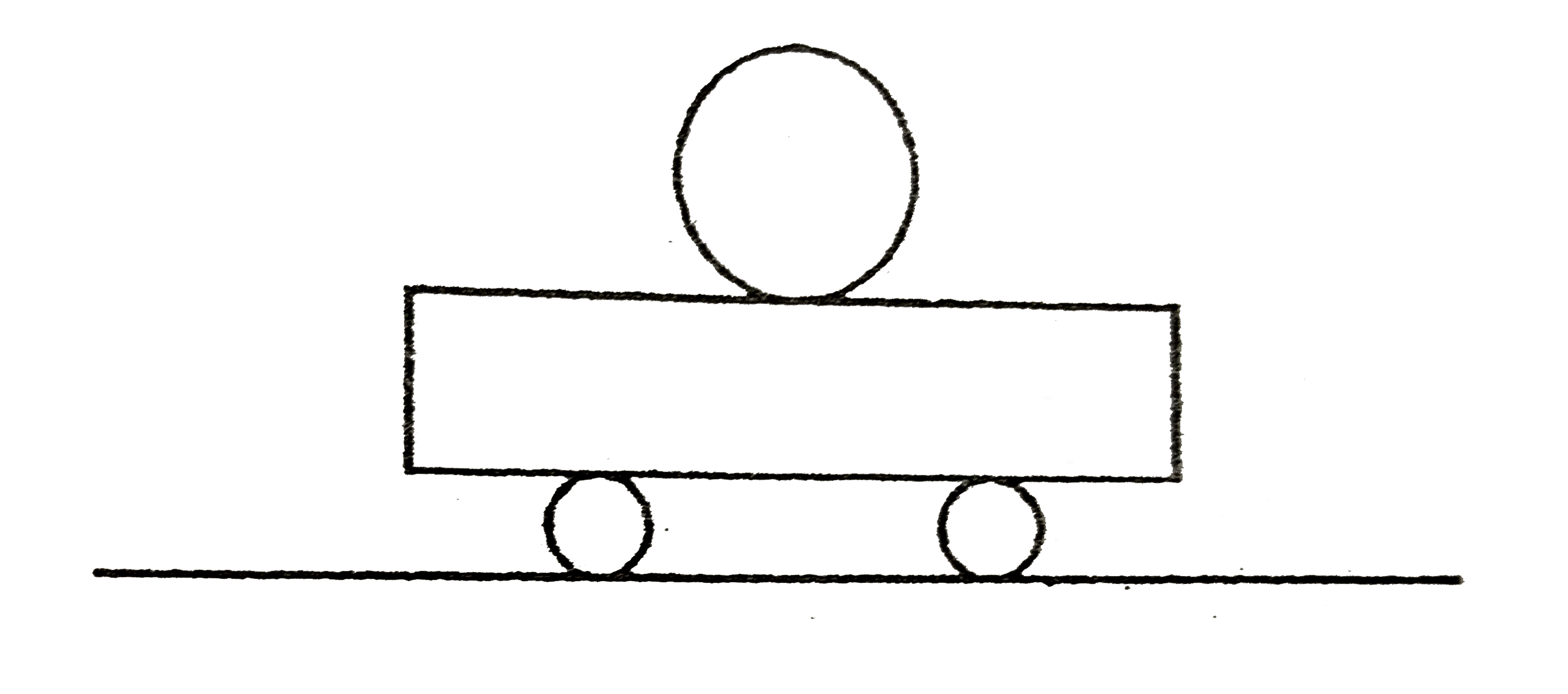
Acceleration of centre of mass of sphere isView Solution


