A man of mass 80kg pushes box of mass 20kg horizontaly. The man moves the box with a constant acceleration of 2m/s2 but his foot does not slip on the ground. There is no friction between the box and the ground. There is no friction between the box and the ground. whereas there is sufficient friction between the man's foot and the ground to prevent him from slipping.
Assertion:- The force applied by the man on the box is equal and opposite to the force applied by the force applid by the box on the man.
Reason:- Friction force applied by the ground on the man is 200N.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are False.
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on both the man and the box, and then apply Newton's laws of motion.
Step 1: Identify the forces acting on the box
The box has a mass of 20 kg and is being pushed by the man with a constant acceleration of 2m/s2. According to Newton's second law, the net force acting on the box can be calculated using the formula:
F=m⋅a
where:
- m is the mass of the box (20 kg)
- a is the acceleration (2 m/s²)
Calculating the force:
F=20kg⋅2m/s2=40N
Step 2: Apply Newton's Third Law
According to Newton's third law of motion, for every action, there is an equal and opposite reaction. This means that the force applied by the man on the box is equal in magnitude and opposite in direction to the force applied by the box on the man.
Thus, if the man exerts a force of F=40N on the box, the box exerts an equal and opposite force of 40N on the man.
Step 3: Analyze the forces acting on the man
The man has a mass of 80 kg. The frictional force that prevents him from slipping is what allows him to push the box. The frictional force must be equal to the force exerted by the box on the man, which we calculated to be 40N.
Step 4: Calculate the frictional force
The frictional force can be calculated as:
Ffriction=mman⋅aman
However, since the man is not accelerating, we can conclude that the frictional force must balance the force exerted by the box on him. Therefore:
Ffriction=40N
Step 5: Evaluate the assertion and reason
- Assertion: The force applied by the man on the box is equal and opposite to the force applied by the box on the man. This is true based on Newton's third law.
- Reason: The friction force applied by the ground on the man is 200 N. This is false because we calculated the frictional force to be 40 N.
Conclusion
The assertion is true, but the reason is false. Therefore, the correct answer is that the assertion is true and the reason is false.
The box has a mass of 20 kg and is being pushed by the man with a constant acceleration of 2m/s2. According to Newton's second law, the net force acting on the box can be calculated using the formula:
F=m⋅a
where:
- m is the mass of the box (20 kg)
- a is the acceleration (2 m/s²)
F=20kg⋅2m/s2=40N
According to Newton's third law of motion, for every action, there is an equal and opposite reaction. This means that the force applied by the man on the box is equal in magnitude and opposite in direction to the force applied by the box on the man.
The man has a mass of 80 kg. The frictional force that prevents him from slipping is what allows him to push the box. The frictional force must be equal to the force exerted by the box on the man, which we calculated to be 40N.
The frictional force can be calculated as:
Ffriction=mman⋅aman
However, since the man is not accelerating, we can conclude that the frictional force must balance the force exerted by the box on him. Therefore:
Ffriction=40N
- Assertion: The force applied by the man on the box is equal and opposite to the force applied by the box on the man. This is true based on Newton's third law.
- Reason: The friction force applied by the ground on the man is 200 N. This is false because we calculated the frictional force to be 40 N.
The assertion is true, but the reason is false. Therefore, the correct answer is that the assertion is true and the reason is false.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3
99 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A man is running on the ground .It is known that the coefficient of friction between the man and the ground is μ . Then which of the following statements is correct
View SolutionIn the arrangement shown in Fig there is no friction between of mass 2m and ground but there is friction between the block of masses m is stationary with respect to block of mass 2m The value of friction between m and 2mis
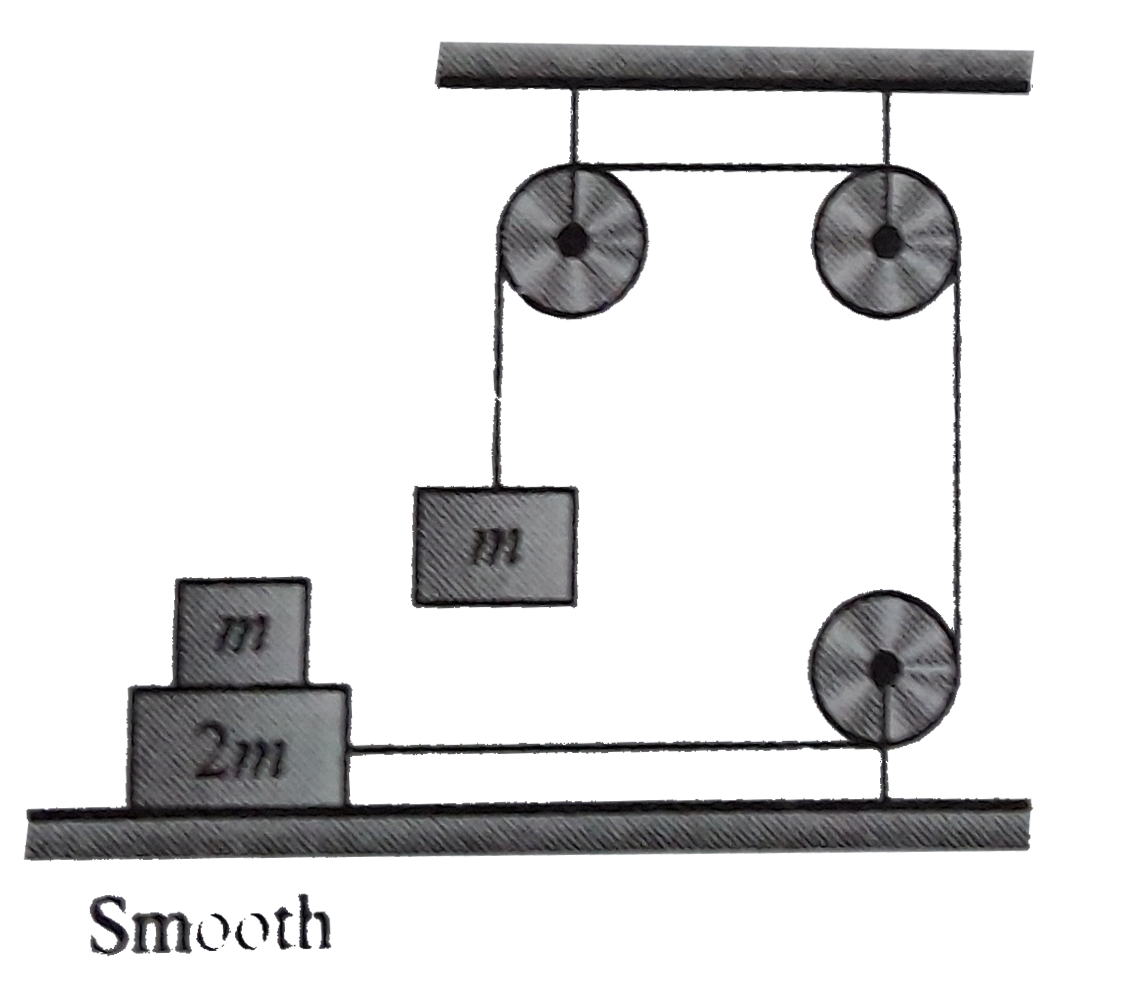
View Solution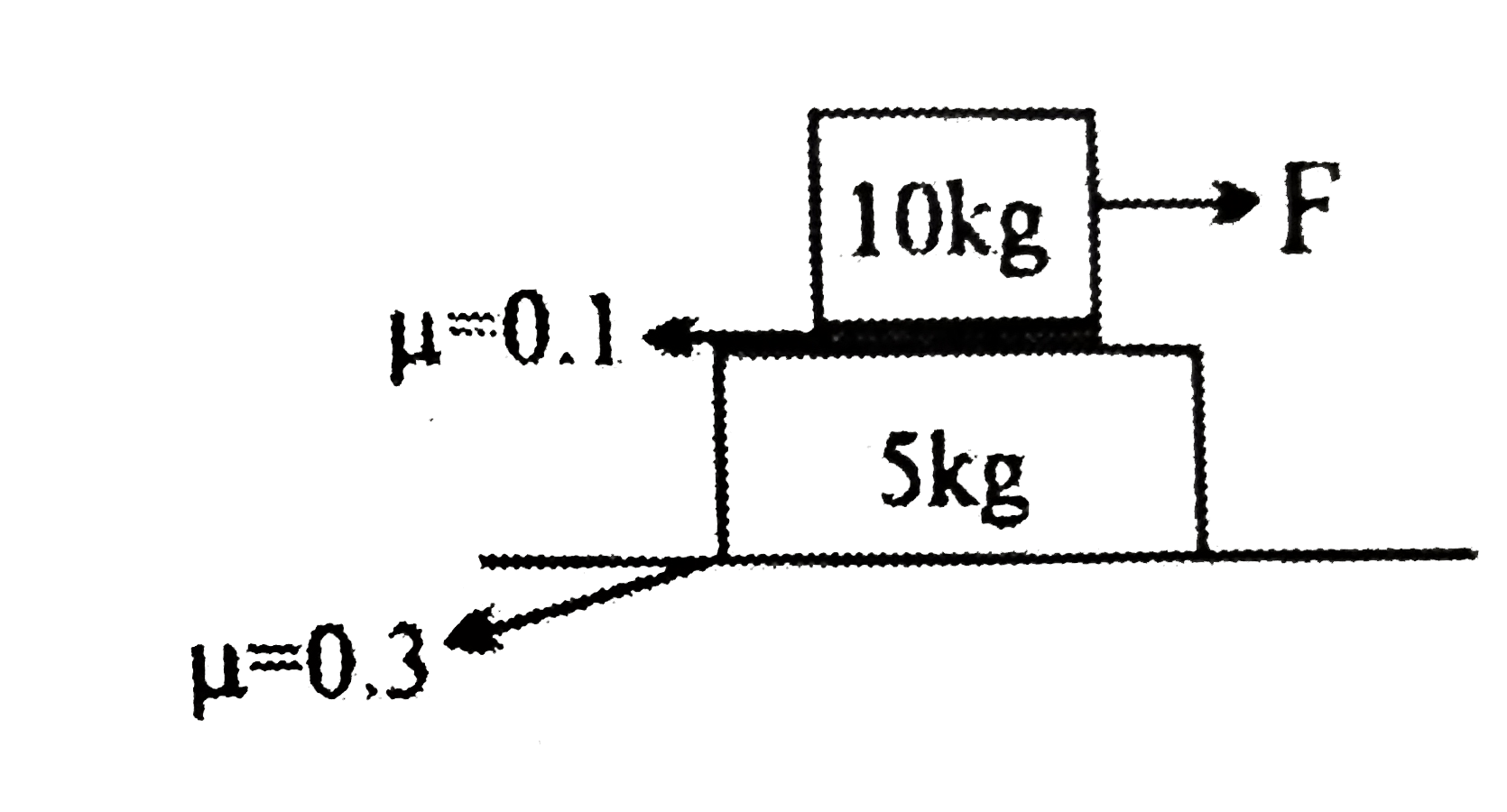
When F = 2N, the frictional force between 5 kg block and ground is
View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is
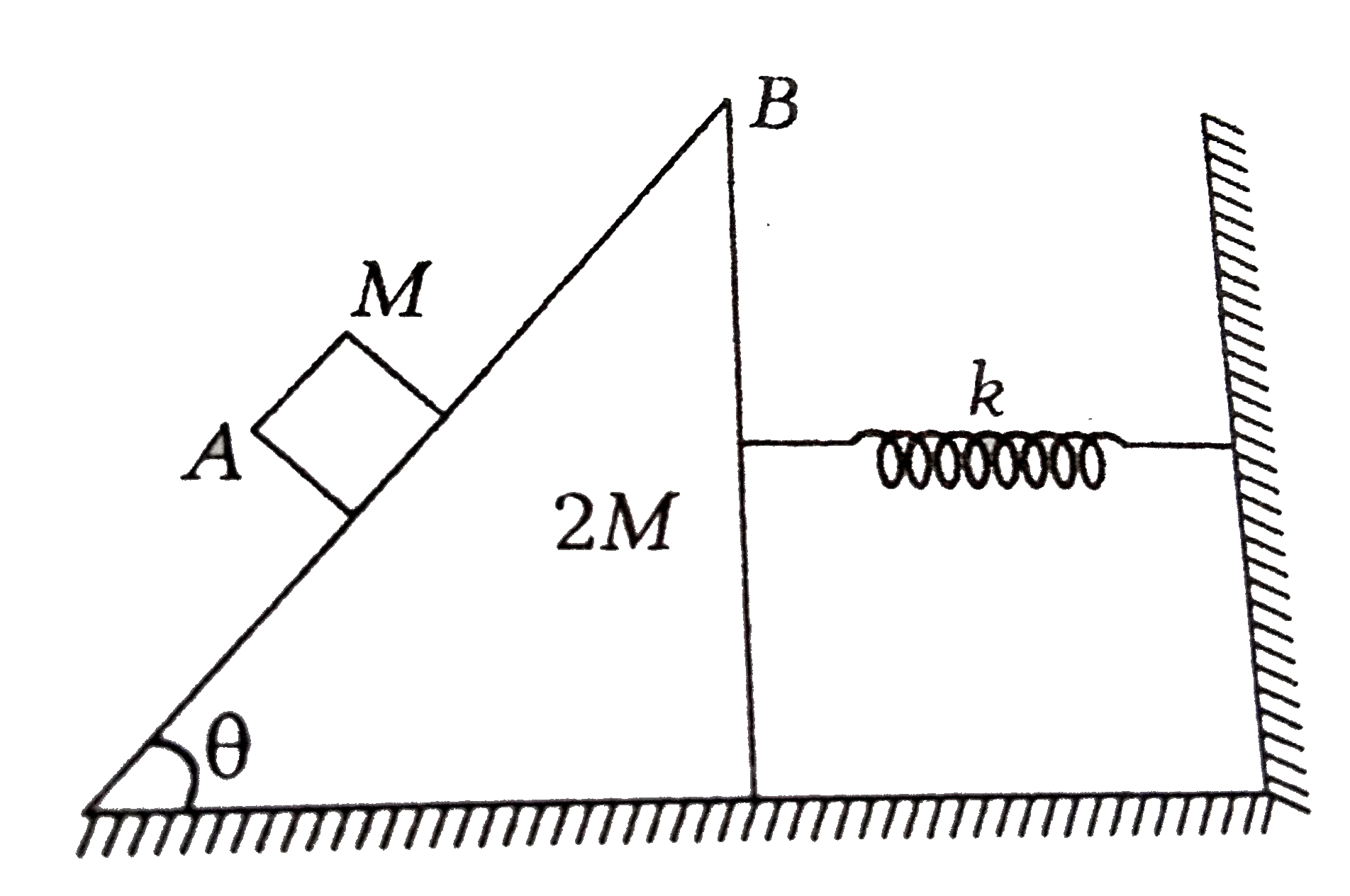
View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
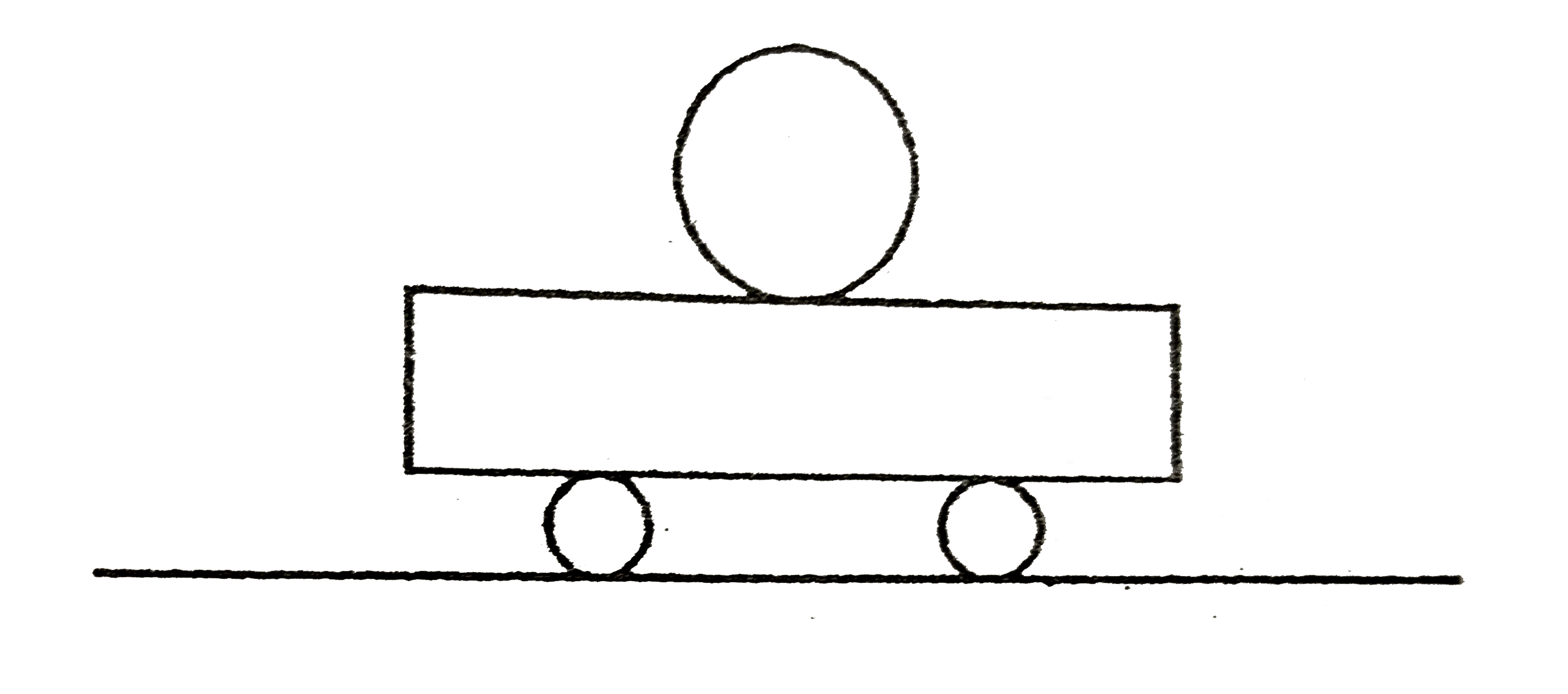
Acceleration of centre of mass of sphere is
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
Angular acceleration of sphere is
View SolutionA ring of mass m and radius R is acted upon by a force Fas shown in figure. There is sufficient friction between the ring and the ground. The force of friction necessary for pure rolling is
View SolutionIn the show arrangement mass of A=1 kg, mass of B= 2kg. Coefficient of friction between A and B =0.2

There is no friction between B and ground. The frictional force exerted by A on B equals.
View Solution
