Mass Center of a sector of a uniform circular plate
Find location of mass center of a sector of a thin uniform plate.
To find the location of the mass center of a sector of a thin uniform circular plate, we can follow these steps:
1. Define the Problem:
We have a sector of a thin uniform circular plate with radius R and subtended angle 2θ. The mass of the plate is m and the mass per unit area is σ.
2. Calculate the Area of the Sector:
The area A of the sector can be calculated using the formula for the area of a circle:
A=12R2θ
where θ is in radians. Since the total angle is 2θ, the area becomes:
A=12R2(2θ)=R2θ
3. Determine the Mass of the Sector:
The mass m of the sector can be expressed in terms of the area and mass per unit area:
m=σ⋅A=σ⋅(R2θ)=σR2θ
4. Set Up the Integral for the Center of Mass:
The center of mass xcm in the x-direction can be calculated using the formula:
xcm=1m∫xdm
For a differential mass element dm at a distance r from the origin, we can express dm in terms of the area element dA:
dm=σdA
The area element dA can be expressed in polar coordinates as:
dA=rdrdθ
5. Integrate to Find the Center of Mass:
The x-coordinate of the center of mass can be expressed as:
xcm=1m∫R0∫θ−θ(rcosθ)σrdrdθ
Since the plate is symmetric about the y-axis, the y-coordinate of the center of mass will be zero.
6. Evaluate the Integral:
The integral simplifies to:
xcm=1σR2θ∫R0∫θ−θr2cosθdrdθ
After evaluating the integral, we find:
xcm=2Rsinθ3θ
7. Final Result:
Thus, the location of the mass center of the sector is:
xcm=2Rsinθ3θ
We have a sector of a thin uniform circular plate with radius R and subtended angle 2θ. The mass of the plate is m and the mass per unit area is σ.
The area A of the sector can be calculated using the formula for the area of a circle:
A=12R2θ
where θ is in radians. Since the total angle is 2θ, the area becomes:
A=12R2(2θ)=R2θ
The mass m of the sector can be expressed in terms of the area and mass per unit area:
m=σ⋅A=σ⋅(R2θ)=σR2θ
The center of mass xcm in the x-direction can be calculated using the formula:
xcm=1m∫xdm
For a differential mass element dm at a distance r from the origin, we can express dm in terms of the area element dA:
dm=σdA
The area element dA can be expressed in polar coordinates as:
dA=rdrdθ
The x-coordinate of the center of mass can be expressed as:
xcm=1m∫R0∫θ−θ(rcosθ)σrdrdθ
Since the plate is symmetric about the y-axis, the y-coordinate of the center of mass will be zero.
The integral simplifies to:
xcm=1σR2θ∫R0∫θ−θr2cosθdrdθ
After evaluating the integral, we find:
xcm=2Rsinθ3θ
Thus, the location of the mass center of the sector is:
xcm=2Rsinθ3θ
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Mass center of a system of a segment of a uniform circular rod(arc)
Find location of mass center of a thin uniform rod bent into shape of an arc.
View SolutionWhat is the location of the centre of mass of a uniform triangular lamina ?
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionFind the centre of mass of a uniform solid cone.
View SolutionFind coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View SolutionIn the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
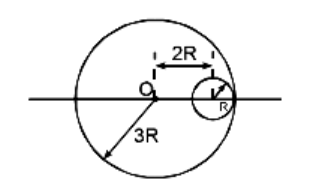
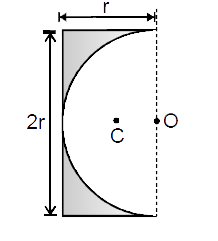
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
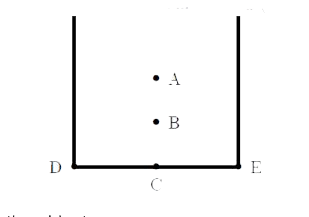
View SolutionA thick uniform wire is bent into the shape of the letter “U” as shown. Which point indicates the location of the center of mass of this wire?
View SolutionThe distance of the centre of mass of T-shaped uniform plate from O is :
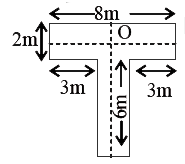
View SolutionThe radius of gyration of a uniform square plate of mass M and sida about its diagonal is
View Solution
