Question

A loaded spring gun, initially at rest on a horizontal frictionless surface, fires a marble at angle of elevation theta. The mass of the gun is M, the mass of the marble is m, and the muzzle velocity of the marble is $v_0$. What is the final motion of the gun ?

Explanation

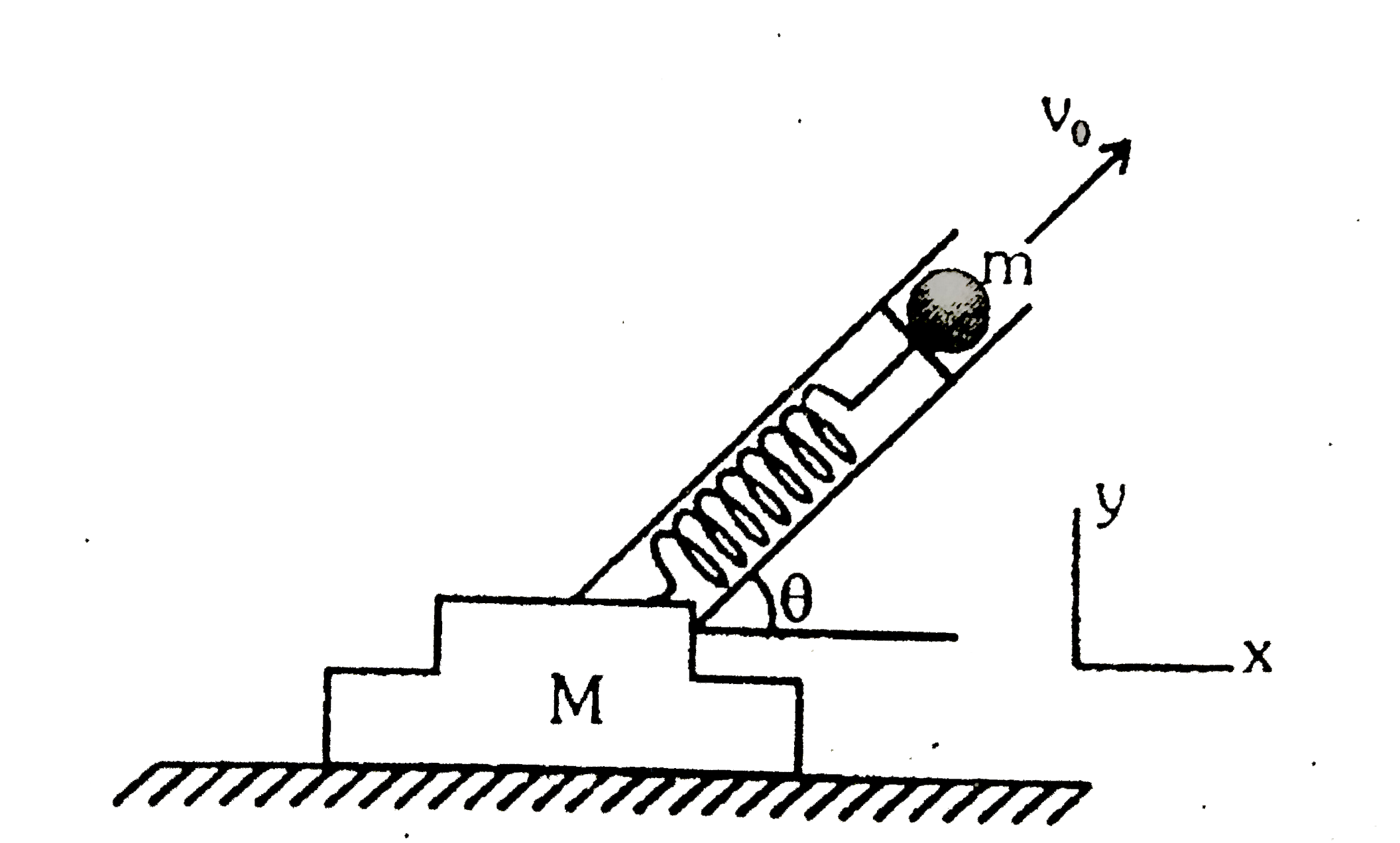
Take the physical system to be the gun and marble. Gravity and the normal force of the table act on the system. Both these forces are vertical. Since there are no horizontal external forces, the x component of the vector equation `F=dP/dt` is `0=dP_x/dt` According to equation (1), `P_x` is conserved:
`P_(x. "initial") = P_(x."final")`
Let the initial time be prior to firing the gun. Then `P_(x."initial") = 0`, since the system is initially at rest. After the marble has left the muzzle, the gun recoils with some speed `V_(1)`, and its final horizontal momentum is `MV_(1)`, to the left. FInding the final velocity of the marble involves a subtle point, however. Physically, the marble's accelaration is due to the force of the gun, and the gun's recoil is due to the reaction force of the marble. The gun stops accelerating once the marble leaves the barrel, so that at the instant the marble and the gun part company, the gun has its final speed `V_(f)`. At that same instant the speed of the marble relative to the gun is `v_(0)`. Hence, the final horizontal speed of the marble relative to the tablet is `v_(0) cos theta-V_(f)`. By conservation of horizontal momentum, we therefore have
`0=m(v_(0)costheta-V_(f))-MV_(f)`
or `V_(f) = (mv_(0)costheta)/(M+m)`
By using conversation of momentum we found the final motion of the system in a few steps. To show the advantage of this method, let us repeat the problem using Newton's laws directly. Let v(t) be the velocity of marble at time t and let `V(t)` be the velocity of the gun. While the marble is going fired, it is acted on by the spring, by gravity, and by friction forces with the muzzle wall. Let the net force on the marble be f(t). The x equation of motion for the marble is
`m(dv_(x))/dt=f_(x)(t)` Formal integration of equation (3) gives
`mv_(x)(t)=mv_(z)(0) + int_(0)^(t) f_(x)dt`
The external forces are all vertical, and therefore the horizontal force `f_(x)` on the marble is due entirely to the gun. By newton's third law, there is a reaction force- `f_(x)` on the gun due to the marble. No other horizontal forces acts on the gun, and the horizontal equation of motion for the gun is therefore `M(dV_x)/(dt)=-f_x(t)`, which can be integrated to give
`MV_(x)(t)=MV_(x)(0) - int_(0)^(t) f_(x)dt` we can eliminate the integral by combining equation (4) and (5).
`MV_(x)(t)+mv_(x)(t)=MV_(x)(0)+mv_(z)(0)`
we have rediscovered that the horizontal component of momentum is conserved. What about the motion of the center of mass? Its horizontal velocity is
`R_(x)(t)=(MV_(x)(t) +mv_(x)(t))/(M+m)` Using equation (6), the numerator can be rewritten to give
`R_(x)(t)=(MV_(x)(0)+mv_(x)(0))/(M+m)=0`
SInce the system is initially at rest. `R_x` is constant, as we expect.
We did not include the small force of air friction. Would the center of mass remain at rest if we had included it? The essential step in our derivation of the law of conservation of momentum was to use Newton's third law. Thus, conservation of momentum appears to be natural consequence of newtonian mechanics. It has been found, however, that conservation of momentum holds true even in areas where newtonian mechanics proves inadequate, including the realms of quantum mechanics and relativity. In addition, conservation of momentumcan be generalized to apply to systems like the electromagnetic field, which possess momentum but not mass. For these reasons, conservation of momentum is generally regarded as being more fundamental than newtonian mechanics. From the point of view, Newton's thitd law is a simple consequance of conservation of momentum for interacting particles. For our present purposes it is purely a matter of taste whether we wish to regard Newton's third law or conservation of momentum as more fundamental.