A block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
A)Angular momentum about A is mvh initially
B)Angular momentum about A is conserved
C)Torque of the forces acting on block is zero about A
D)Block will eventually stop and angular momentum conservation is not applicable here
To solve the problem, we need to analyze the motion of the block on the rough surface and its angular momentum about point A. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
- We have a block of mass m moving with an initial velocity v on a rough horizontal surface.
- The height of the center of mass of the block is h from the surface.
- We need to consider the angular momentum of the block about point A on the surface.
Hint: Identify the parameters given in the problem and visualize the scenario.
Step 2: Calculate the Initial Angular Momentum
- The angular momentum L of a particle about a point is given by the formula:
L=r×p
where r is the distance from the point to the line of action of the velocity vector, and p is the linear momentum of the block.
- The linear momentum p of the block is:
p=mv
- The distance r from point A to the center of mass of the block is equal to h (the height of the center of mass) because point A is on the surface.
Thus, the initial angular momentum L about point A is:
L=m⋅v⋅h
Hint: Use the formula for angular momentum and remember that the distance to the line of action is crucial.
Step 3: Analyze the Effect of Friction
- As the block moves, it experiences friction, which will cause it to decelerate.
- The frictional force acts opposite to the direction of motion, reducing the velocity v over time.
- Eventually, the block will stop due to the work done against friction.
Hint: Consider how friction affects the motion of the block and its velocity over time.
Step 4: Determine the Conservation of Angular Momentum
- Angular momentum is conserved only when there is no net external torque acting on the system.
- In this case, since the block is experiencing friction, which is an external force, the angular momentum about point A is not conserved.
- Initially, the angular momentum is mvh, but as the block slows down, this value will change.
Hint: Recall the conditions for conservation of angular momentum and apply them to the presence of external forces.
Step 5: Conclusion
- The initial angular momentum of the block about point A is mvh.
- However, due to friction, the angular momentum is not conserved as the block will eventually stop.
Final Statement: The angular momentum of the block about point A is initially mvh, but it is not conserved due to the external torque caused by friction.
- We have a block of mass m moving with an initial velocity v on a rough horizontal surface.
- The height of the center of mass of the block is h from the surface.
- We need to consider the angular momentum of the block about point A on the surface.
- The angular momentum L of a particle about a point is given by the formula:
L=r×p
where r is the distance from the point to the line of action of the velocity vector, and p is the linear momentum of the block.
- The linear momentum p of the block is:
p=mv
- The distance r from point A to the center of mass of the block is equal to h (the height of the center of mass) because point A is on the surface.
L=m⋅v⋅h
- As the block moves, it experiences friction, which will cause it to decelerate.
- The frictional force acts opposite to the direction of motion, reducing the velocity v over time.
- Eventually, the block will stop due to the work done against friction.
- Angular momentum is conserved only when there is no net external torque acting on the system.
- In this case, since the block is experiencing friction, which is an external force, the angular momentum about point A is not conserved.
- Initially, the angular momentum is mvh, but as the block slows down, this value will change.
- The initial angular momentum of the block about point A is mvh.
- However, due to friction, the angular momentum is not conserved as the block will eventually stop.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - E) Assertion-Reason Type Questions
12 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)
60 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
Asseration : A block of mass m starts moving on a rough horizontal surface with a velocity v. It stops due to friction between the block and the surface after moving through a ceratin distance. The surface is now tilted to an angle of 30∘ with the horizontal and same block is made to go up on the surface with the same initial velocity v. The decrease in the mechanical energy in the second situation is small than the first situation.
Reason : The coefficient of friction between the block and the surface decreases with the increase in the angle of inclination.
View SolutionA solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
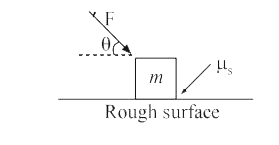
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
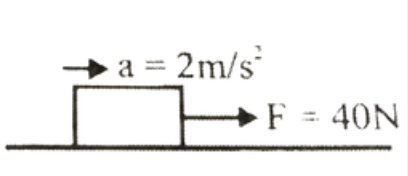
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
View SolutionA uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
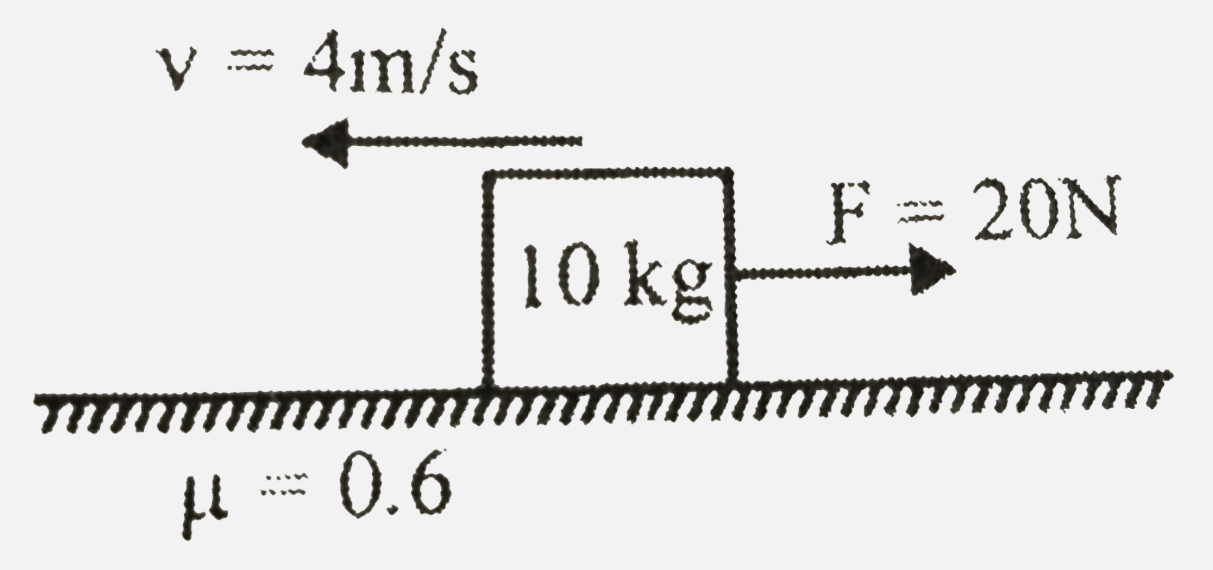
View SolutionA block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution
