A disk sliding with velocity u on a smooth horizontal plane strikes another identical disk kept at rest as shown in the figure. If the impact between the disks is perfectly elastic impact, find velocities of the disks after the impact.
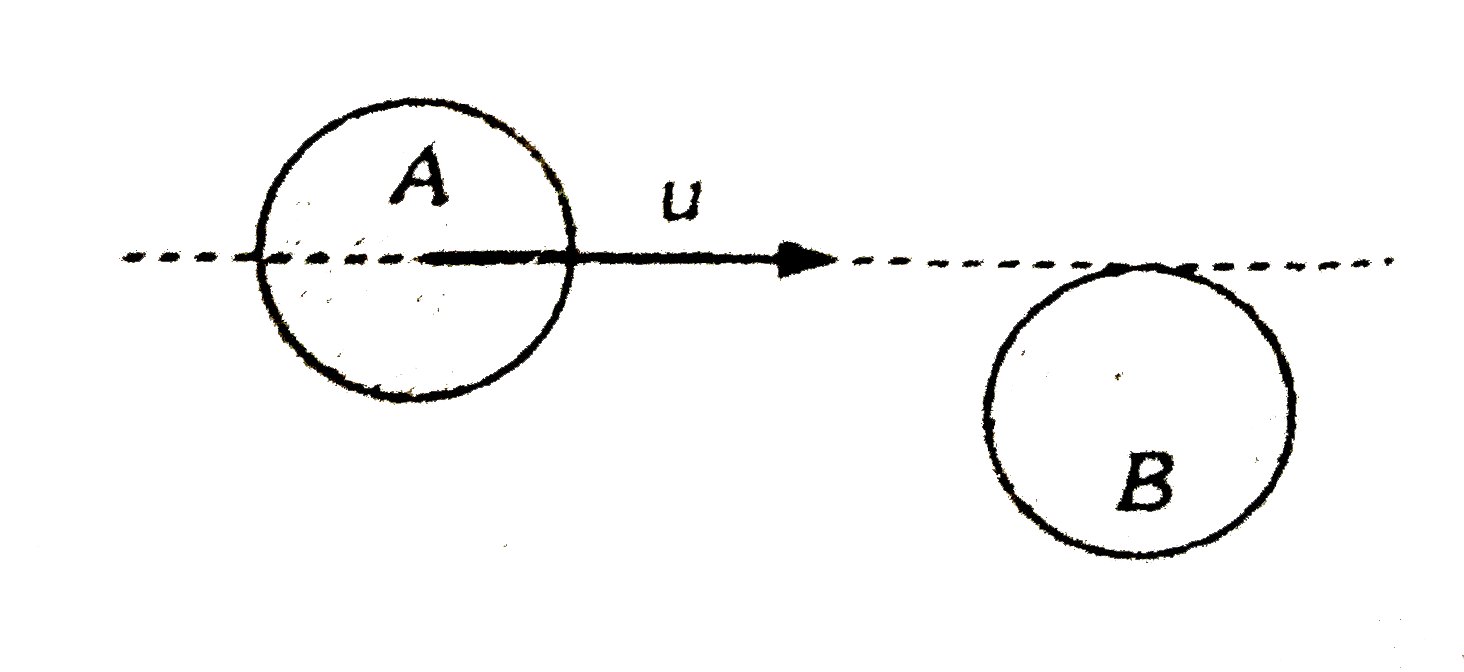
We first show velocity components along the t and the n-axis immediately before and after the impact. Angle that the line of impact makes with velocity u is 30∘

Component along t-axis Components of momentum along the t-axis of each disk, considered separately, is conserved. Hence, t-component of velocities of each of the bodies remains unchanged.
vAt=uAt=u2 and vBt=uBt=0 ...(i)
The component along the n-axis of the total momentum of the two bodies is conserved
mBvBn+mAvAn=mBuBn+mAuAn→mvBn+mvAn=m×0+mu√32
vBn+vAn=u√32 ...(ii)
Concept of coefficient of restitution e is applicable only for the n-component velocities.
vBn−VAn=e(uAn−UBn)→ vBn−VAn=u√32 ...(iii)
From equations (ii) and (iii), we have vAn=0 and vBn=u√32 ...(iv)
From equations (i) and(iv) we can write velocities of both the disks.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II43videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A sphere of mass m slides with velocity v on as frictionless surface towards a smooth inclined wall as shown in figure. If the collision with the wall is perfectly elastic find a. the impulse imparted by the wall on the sphere b the impulse imparted by the floor on the sphere.
 View Solution
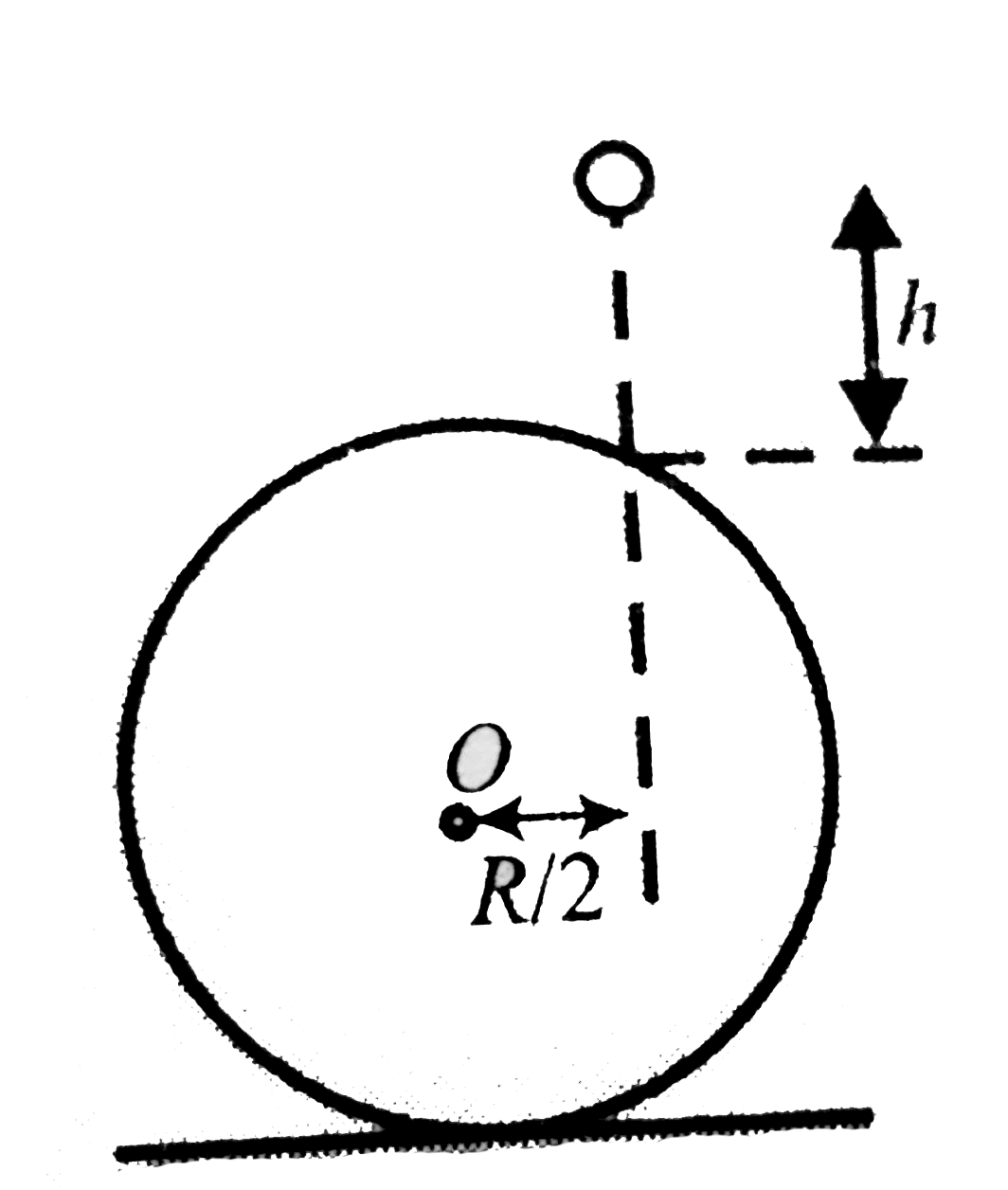
View SolutionA small particle of mass m is released from a height h on a large smooth sphere kept on a perfectly smooth surface as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.
 View Solution
View SolutionA ping-pong ball strikes a wall with a velocity of 10ms−1. If the collision is perfectly elastic, find the velocity if ball after impact
View Solution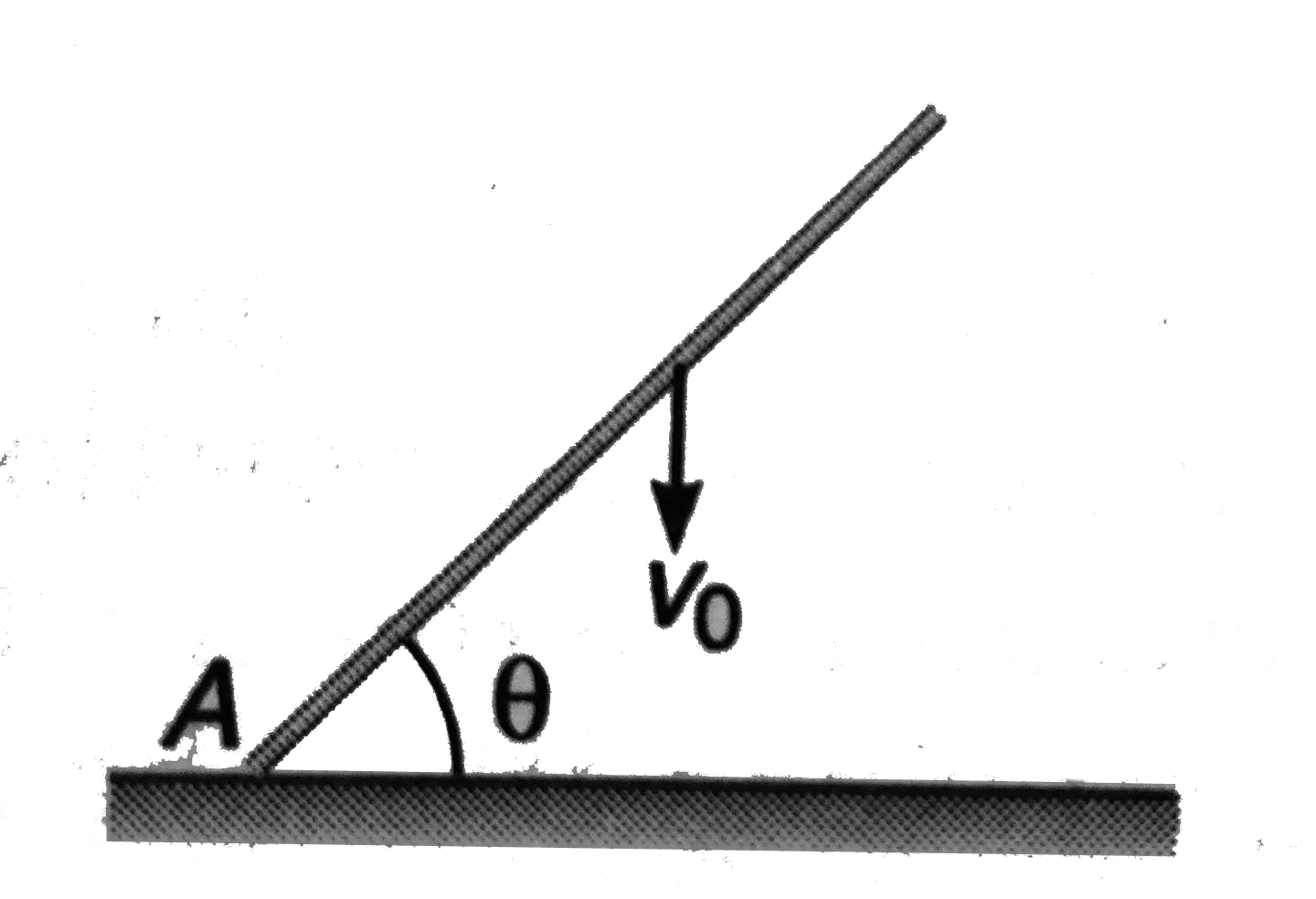
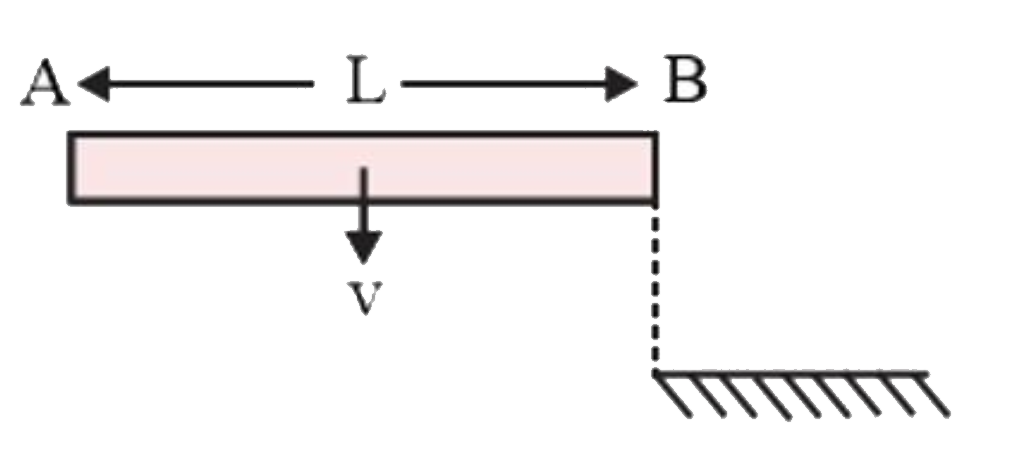
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
 View Solution
View SolutionA triangular wedge of mass M is moving with uniform velocity v0 along a smooth horizontal surface in the leftward direction. A particle of mass m falls from rest from height h onto the inclined face, colliding elastically with it. Find velocity of the ball and wedge after the impact taking M = 2m.
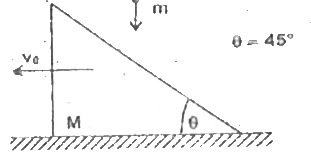 View Solution
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
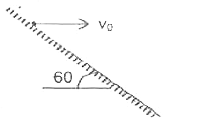 View Solution
View SolutionAn object is moving towards a mirror with a velocity of 10ms−1 as shown in the figure. If the collision between the mirror and the object is perfectly elastic, then the velocity of the image after collision with mirror in vector form is
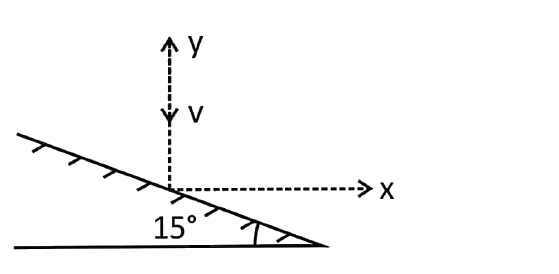 View Solution
View SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
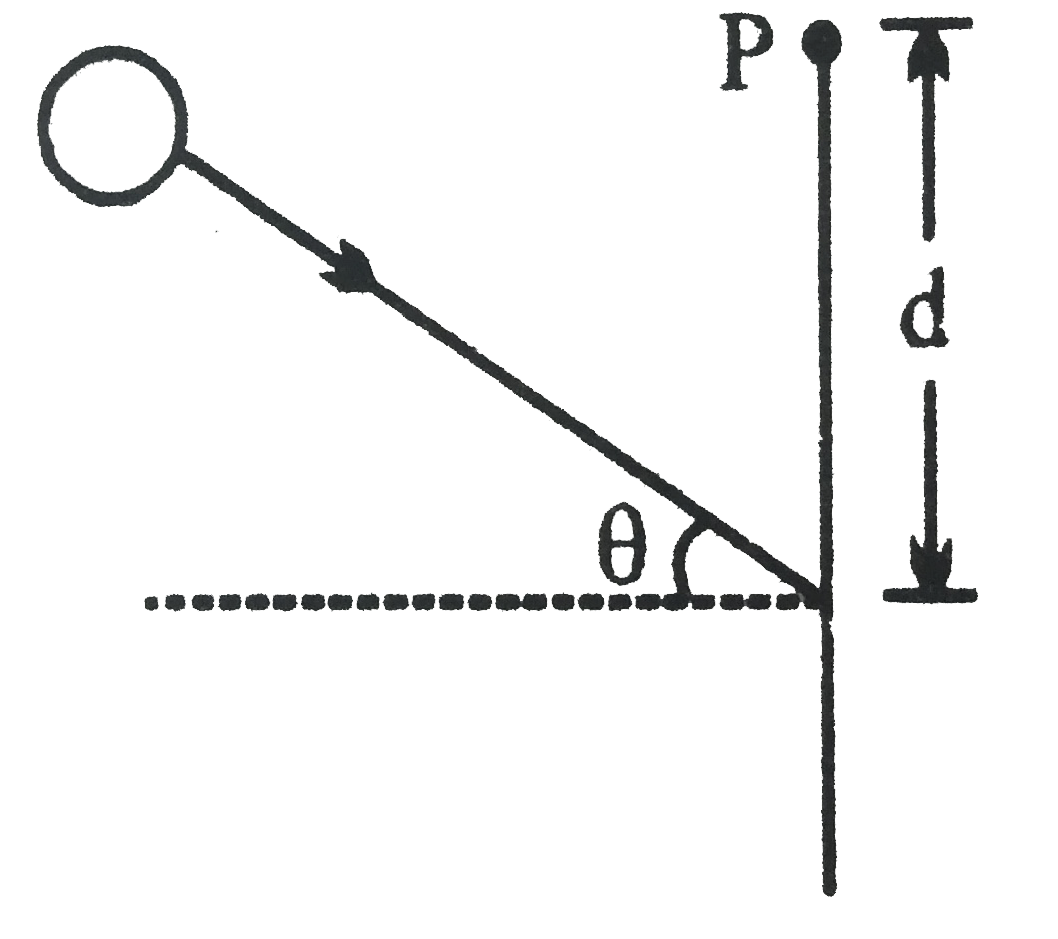 .View Solution
.View SolutionA rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

The distance of point P from centre of the rod which is at rest just after impact isView Solution

