A small particle of mass m is released from a height h on a large smooth sphere kept on a perfectly smooth surface as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.
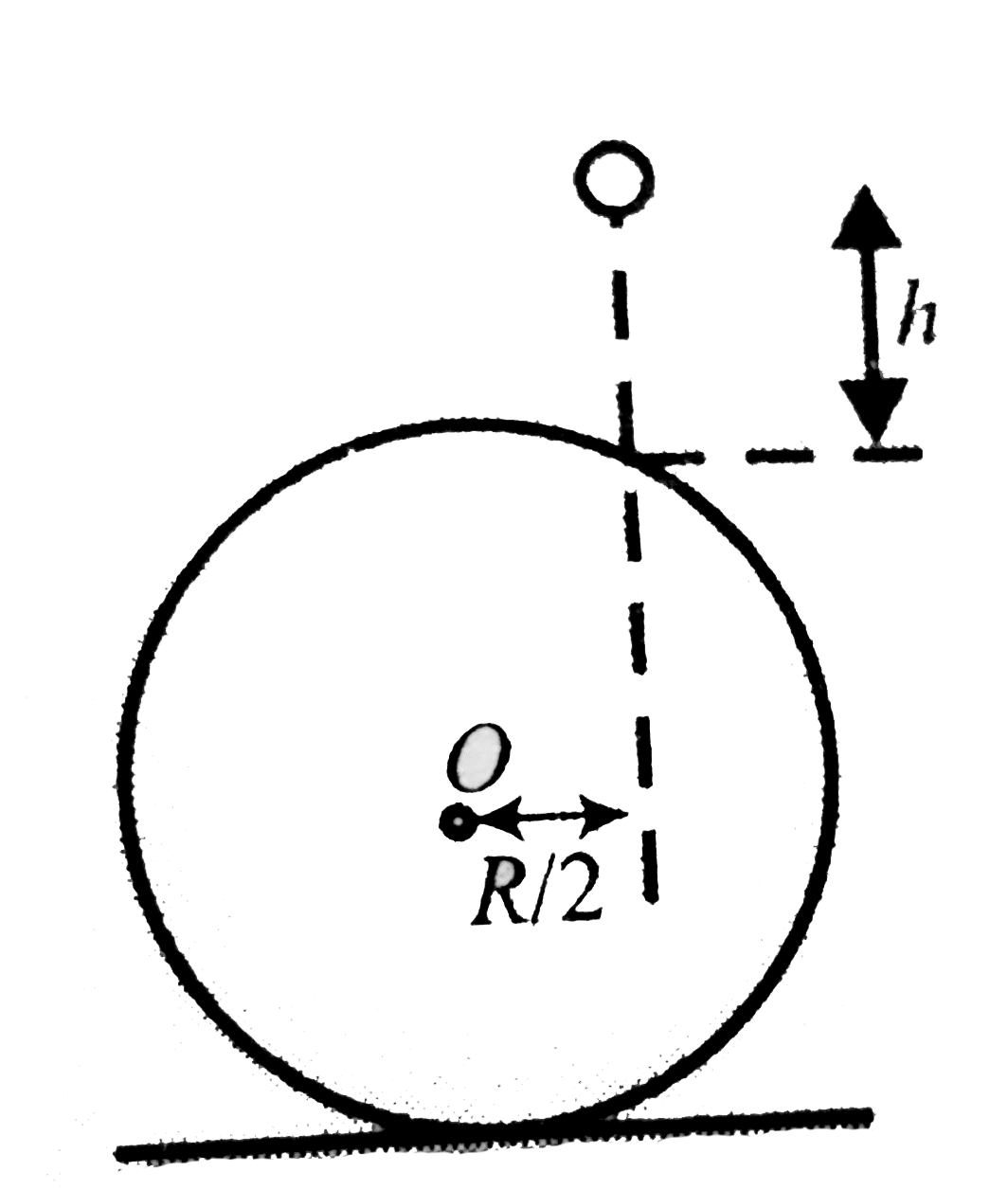
Collision takes lace between smooth bodies, therefore, tangential velocity of particle is unchanged.
vr=usinθ and u=√2gh
when sinθ=R2R=12 or θ=30∘
vt=u2 …………i

From conservation of momentum along x-axis,
Pi=Pf
0+0=MV+mvnsinθ+mvtcosθ..............iii
from the definitation of coefficient of restitution.
e=Vsinθ−(−vn)ucoshtη−0=0
[e=0, for a perfectly inelastic collision]
or, Vsinθ=−vn
vn=−V2 .............iii
On substitution expression for vn and vt in eqn ii we obtain
MV=m(−V2)12+m(u2)√32
(M+m4)V=mu√34
where u=√2gh or V=m√6gh(4M+m)
v=√v2n+v2t=
⎷6m2gh4(4M+m)2+gh2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A particle of mass m is released from a height H on a smooth curved surface which ends into a vertical loop of radius R, as shown. Choose the correct alernative(s) if H=2R.
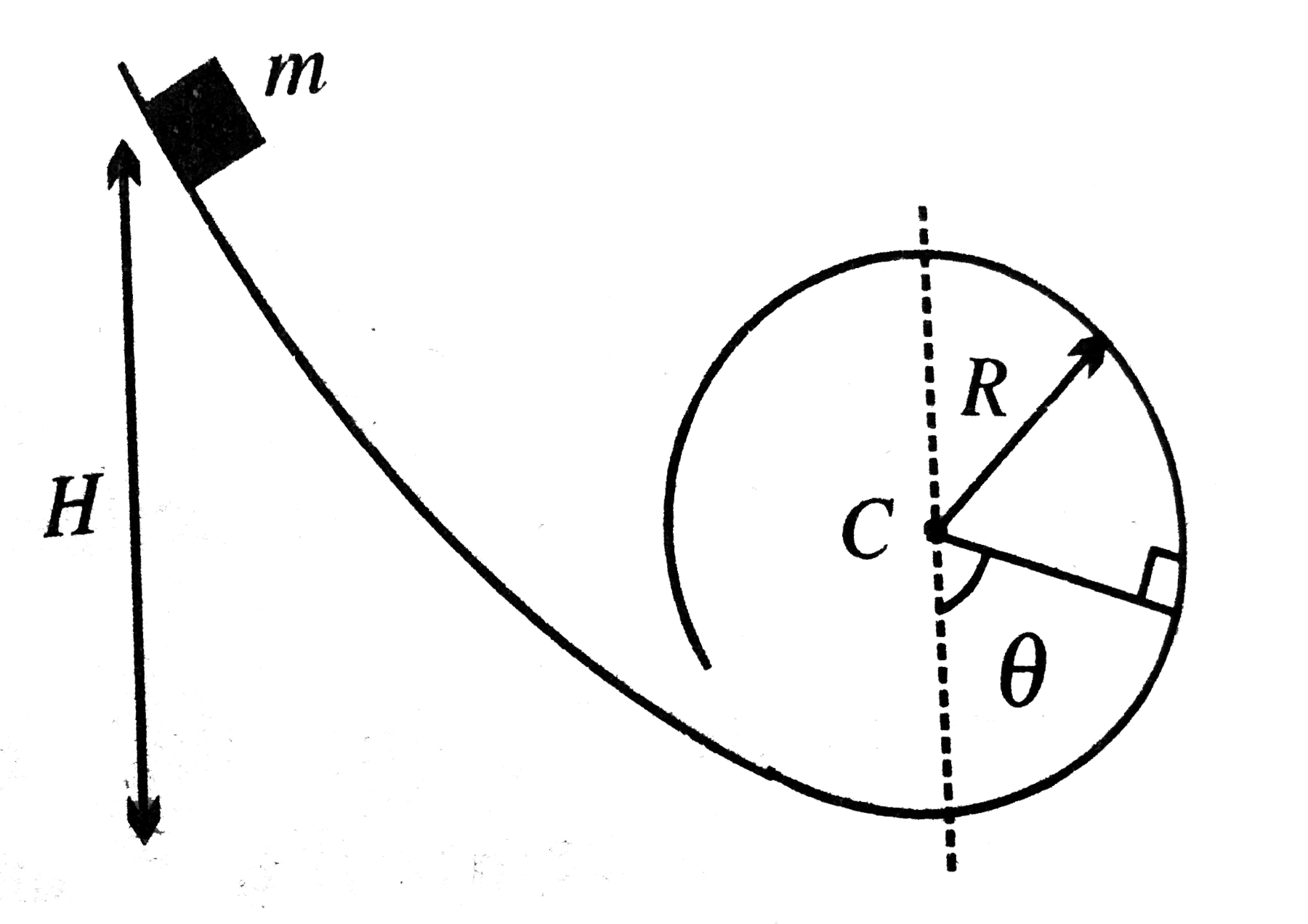
View SolutionA particle of mass m is released from a height H on a smooth curved surface which ends into a vertical loop of radius R, as shown. Choose the correct alernative(s) if H=2R.
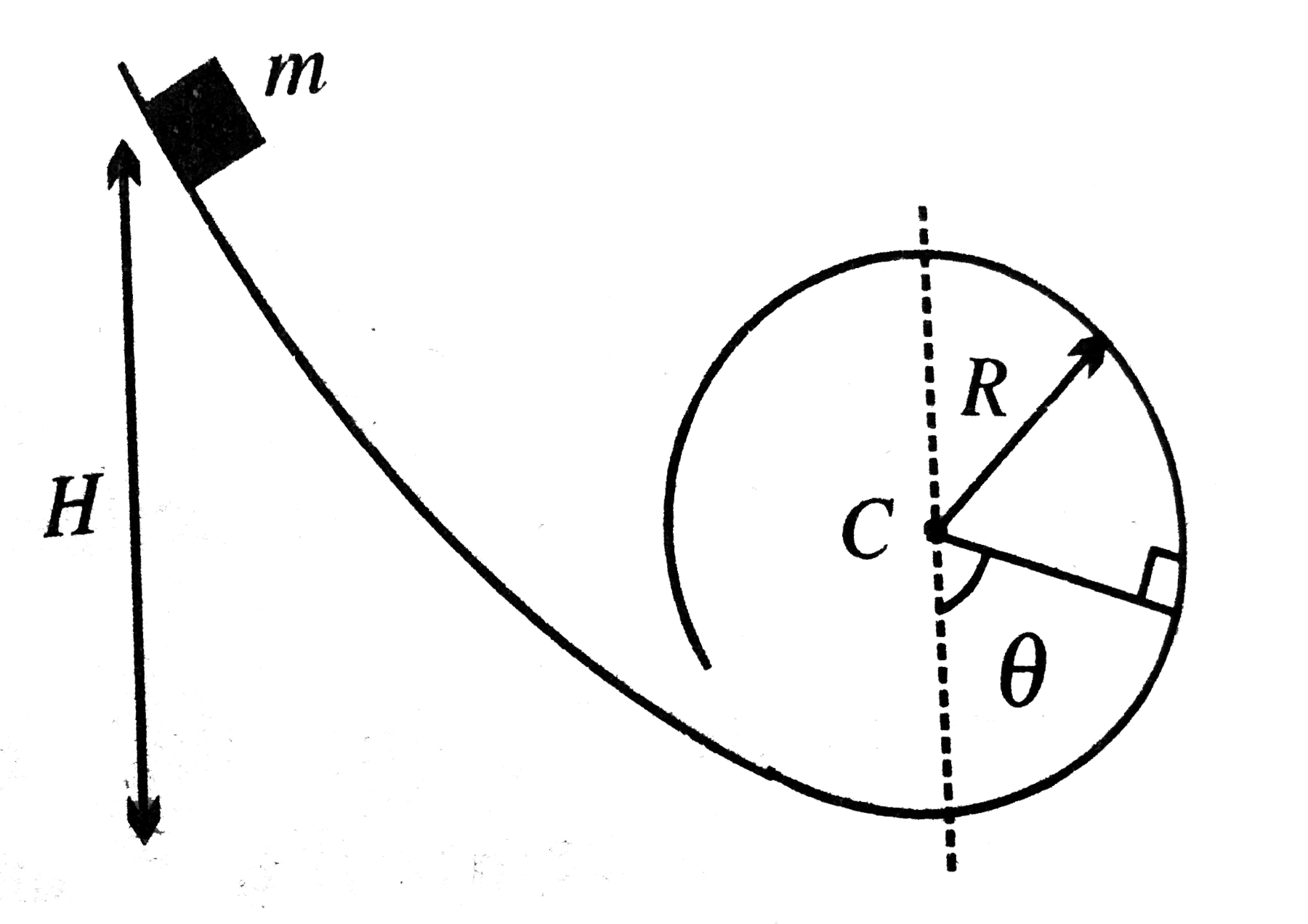
View Solution
Knowledge Check
A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘
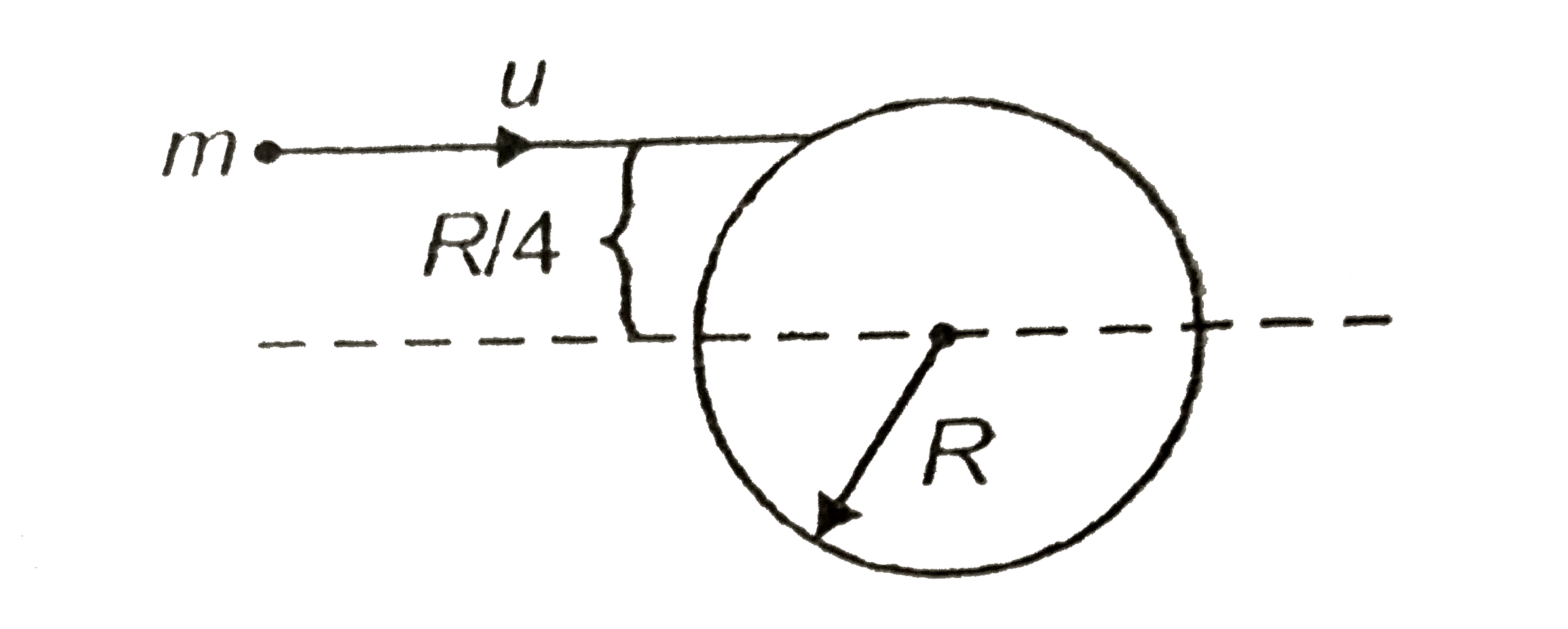
A particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
View SolutionThere are two identical particles A and B. One is projected vertically upward with speed √2gh from ground and other is dropped from height h along the same vertical line. Collision between them is perfectly inelastic. Find time taken by them to reach the ground after collision in terms of √hg.
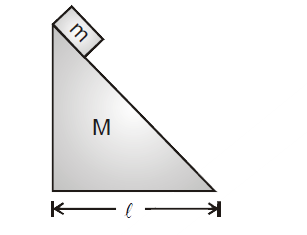
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
View SolutionA sphere of mass m slides with velocity v on as frictionless surface towards a smooth inclined wall as shown in figure. If the collision with the wall is perfectly elastic find a. the impulse imparted by the wall on the sphere b the impulse imparted by the floor on the sphere.

View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collision
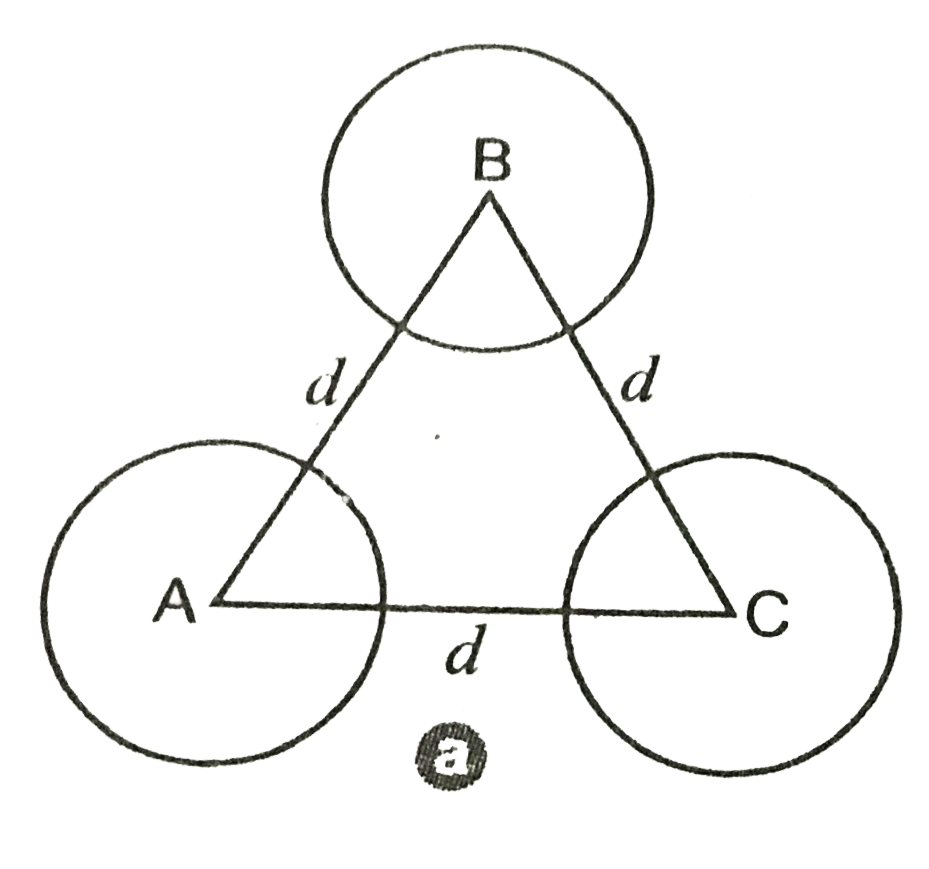
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View SolutionA body of mass m is dropped from a height of h. Simultaneously another body of mass 2m is thrown up vertically with such a velocity v that they collide at height h2. If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
View Solution
