A ball moving vertically downward with a speed of 10m/s collides with a platform. The platform moves with a velocity of 5m/s in downward direction. If e=0.8, find the speed (in m/s ) of the ball just after collision.
The correct Answer is:1m/s
To solve the problem, we will use the concept of the coefficient of restitution (e), which relates the velocities of two objects before and after a collision. The formula for the coefficient of restitution is given by:
e=v2−v1u1−u2
Where:
- e is the coefficient of restitution
- v2 is the final velocity of the ball after the collision
- v1 is the final velocity of the platform after the collision (which is 5m/s downward)
- u1 is the initial velocity of the ball before the collision (which is 10m/s downward)
- u2 is the initial velocity of the platform before the collision (which is 5m/s downward)
1. Identify the velocities:
- Initial velocity of the ball, u1=−10m/s (downward is negative)
- Initial velocity of the platform, u2=−5m/s (downward is negative)
- Final velocity of the platform after collision, v1=−5m/s (it continues moving downward)
2. Substitute values into the restitution formula:
e=0.8=v2−(−5)−10−(−5)
3. Simplify the equation:
0.8=v2+5−10+5
0.8=v2+5−5
4. Multiply both sides by -5:
−4=v2+5
5. Solve for v2:
v2=−4−5
v2=−9m/s
6. Interpret the result:
The negative sign indicates that the ball is moving downward after the collision. Therefore, the speed of the ball just after the collision is 9m/s.
Final Answer:
The speed of the ball just after the collision is 9m/s downward.
- e is the coefficient of restitution
- v2 is the final velocity of the ball after the collision
- v1 is the final velocity of the platform after the collision (which is 5m/s downward)
- u1 is the initial velocity of the ball before the collision (which is 10m/s downward)
- u2 is the initial velocity of the platform before the collision (which is 5m/s downward)
- Initial velocity of the ball, u1=−10m/s (downward is negative)
- Initial velocity of the platform, u2=−5m/s (downward is negative)
- Final velocity of the platform after collision, v1=−5m/s (it continues moving downward)
e=0.8=v2−(−5)−10−(−5)
0.8=v2+5−10+5
0.8=v2+5−5
−4=v2+5
v2=−4−5
v2=−9m/s
The negative sign indicates that the ball is moving downward after the collision. Therefore, the speed of the ball just after the collision is 9m/s.
The speed of the ball just after the collision is 9m/s downward.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II43videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A ball is thrown vertically downward with velocity of 20 m/s from top of tower. It hits ground after some time with a velocity of 80 m /s . Height of tower is
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionA small ball falling vertically downward with constant velocity 4m/s strikes elastically a massive inclined cart moving with velocity 4m/s horizontally as shown. The velocity of the rebound of the ball is
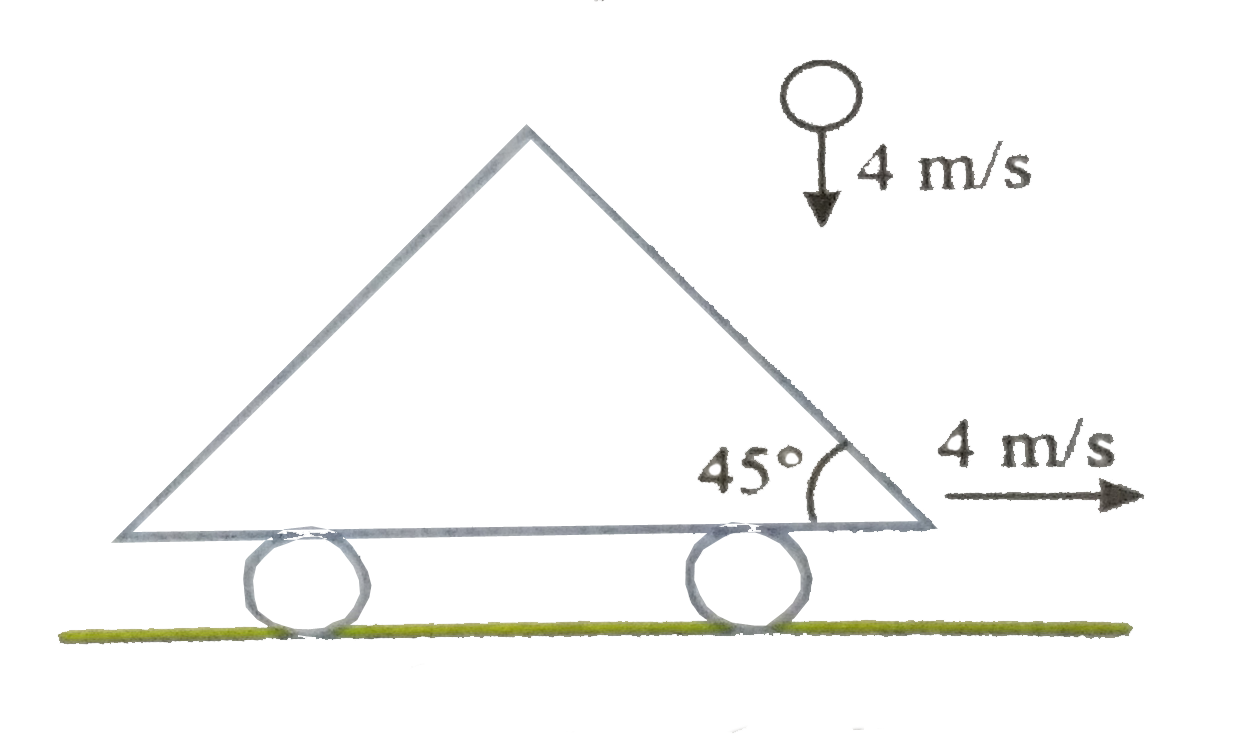 View Solution
View SolutionA ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient of restitution is 2/3. Find the velocities of both ball after the collision.
View SolutionA ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View SolutionA ball is projected vertically up wards with a velocity of 100 m/s. Find the speed of the ball at half the maximum height. (g=10m/s2)
View SolutionA man in a balloon throws a stone downwards with a speed of 5m/s with respect to balloon. The balloon is moving upwards with a constant acceleration of 5m/s2. Then velocity of the stone relative to the man after 2 seconds is.
 View Solution
View SolutionRain is falling vertically downward with velocity 4m/s. A man is moving horizontally with velocity 3m/s, the velocity of rain with respect to man is
View SolutionA small ball falling vertically downward with constant velocity 2m/s strikes elastically an inclined plane moving with velocity 2m/s as shown in figure. The velocity of rebound of the ball with respect ground is
(A)4m/s (B)2√5m/s (C)2√2m/s (D)2m/s View Solution
View Solution

