An object A of mass 1kg is projected vertically upward with a speed of 20m/s. At the same moment another object B of mass 3kg, which in intially above the object A, is dropped from a height h=20m. The two point like objects (A and B) collision and stick to each other. The kinetic energy is K (in J) of the combined mass after collision, find the value of K/25.
The correct Answer is:2
To solve the problem step by step, we will analyze the motion of both objects A and B, calculate their velocities just before the collision, and then find the kinetic energy of the combined mass after the collision.
Step 1: Determine the time of collision
Object A is projected upward with an initial speed of 20m/s and object B is dropped from a height of 20m. We need to find the time t it takes for them to collide.
Using the relative motion concept:
- The relative displacement between A and B is 20m.
- The relative velocity of A with respect to B is 20m/s (upward).
Using the formula for relative motion:
Relative Displacement=Relative Velocity×t
20=20×t
t=1s
Step 2: Calculate the velocity of object A just before the collision
Using the equation of motion for object A:
VA=UA+aA⋅t
Where:
- UA=20m/s (initial velocity of A)
- aA=−10m/s2 (acceleration due to gravity acting downward)
- t=1s
Calculating VA:
VA=20+(−10)⋅1=20−10=10m/s
Step 3: Calculate the velocity of object B just before the collision
Using the equation of motion for object B:
VB=UB+aB⋅t
Where:
- UB=0m/s (initial velocity of B)
- aB=−10m/s2 (acceleration due to gravity acting downward)
- t=1s
Calculating VB:
VB=0+(−10)⋅1=−10m/s
Step 4: Apply conservation of momentum
The total momentum before the collision must equal the total momentum after the collision.
Before the collision:
Total momentum=mA⋅VA+mB⋅VB
Where:
- mA=1kg
- mB=3kg
Calculating total momentum:
Total momentum=1⋅10+3⋅(−10)=10−30=−20kg m/s
After the collision, the combined mass is mA+mB=4kg and let the final velocity be Vf:
Total momentum after collision=(mA+mB)⋅Vf=4⋅Vf
Setting the total momentum before and after equal:
−20=4⋅Vf
Solving for Vf:
Vf=−204=−5m/s
Step 5: Calculate the kinetic energy of the combined mass after the collision
The kinetic energy K of the combined mass is given by:
K=12(mA+mB)V2f
Substituting the values:
K=12⋅4⋅(−5)2=12⋅4⋅25=2⋅25=50J
Step 6: Find the value of K/25
K25=5025=2
Final Answer
The value of K/25 is 2.
---
Object A is projected upward with an initial speed of 20m/s and object B is dropped from a height of 20m. We need to find the time t it takes for them to collide.
- The relative displacement between A and B is 20m.
- The relative velocity of A with respect to B is 20m/s (upward).
Relative Displacement=Relative Velocity×t
20=20×t
t=1s
Using the equation of motion for object A:
VA=UA+aA⋅t
Where:
- UA=20m/s (initial velocity of A)
- aA=−10m/s2 (acceleration due to gravity acting downward)
- t=1s
VA=20+(−10)⋅1=20−10=10m/s
Using the equation of motion for object B:
VB=UB+aB⋅t
Where:
- UB=0m/s (initial velocity of B)
- aB=−10m/s2 (acceleration due to gravity acting downward)
- t=1s
VB=0+(−10)⋅1=−10m/s
The total momentum before the collision must equal the total momentum after the collision.
Total momentum=mA⋅VA+mB⋅VB
Where:
- mA=1kg
- mB=3kg
Total momentum=1⋅10+3⋅(−10)=10−30=−20kg m/s
Total momentum after collision=(mA+mB)⋅Vf=4⋅Vf
Setting the total momentum before and after equal:
−20=4⋅Vf
Solving for Vf:
Vf=−204=−5m/s
The kinetic energy K of the combined mass is given by:
K=12(mA+mB)V2f
Substituting the values:
K=12⋅4⋅(−5)2=12⋅4⋅25=2⋅25=50J
K25=5025=2
The value of K/25 is 2.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II43videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
An object is thrown vertically upward with a speed of 30 m/s. The velocity of the object half-a-second before it reaches the maximum height is
View SolutionAn object of mass 15kg is moving with a uniform velocity of 4m/s. what is the kinetic energy possessed by the object ?
View SolutionA particle of mass 2 kg is projected vertically upward with a velocity of 20 m/s. It attains maximum height of 17 m. The loss in mechanical energy due to air drag is (g=10ms−2)
View SolutionA body of mass 2kg is projected upward from the surface of the ground at t=0 with a velocity of 20m/s. One second later a body B, also of mass 2kg, is dropped from a height of 20m. If they collide elastically, then velocities just after collision are :-
View SolutionTwo objects each of mass 5 kg are moving in the same straight line but in the opposite direction towards each other with some speed of 3 m/s. They stick to each other after collision. What will be the velocity of the combined object after collision?
 View Solution
View SolutionTwo object, each of mass 1.5kg, are moving in the same straight line but in opposite directions, The velocity of each object is 2.5ms−1 before the collision during which they stick together. What will be the velocity of the combined object after collision?
View SolutionAn object of mass M1 moving horizontally with speed u colides elstically with another object of mass M2 at rest. Select correct statement.
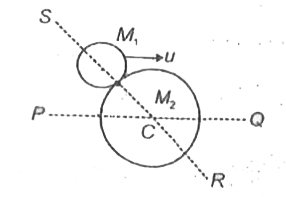 View Solution
View SolutionTwo particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
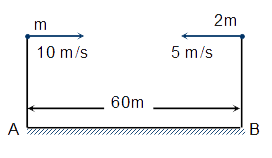 View Solution
View SolutionAn object of mass 10 kg is projected from ground with speed 40 m/s at an angle 60∘ with horizontal the rate of change of momentum of object one second after projection in SI unit is
[ Take g = 9.8 m/s2 ]View SolutionA body of mass 10 kg and velocity 10 m/s collides with a stationary body of mass 5 kg . After collision both bodies stick to each other , velocity of the bodies after collision will be
View Solution

