Distance of the centre of mass of a solid uniform cone from its vertex is Z0. If the radius of its base is R and its height is h then Z0 is equal to :
5h80
3h28R
h24R
3h4
The correct Answer is:A
for solid cone c.m. is h4 from base
so z0=h−h4=3h4
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Knowledge Check
The centre of gravity of a hollow cone of height h is at distance x from its vertex where the value of x is:
Ah/3Bh/4C2h/3D3h/4
The centre of mass of a solid cone along the line form the center of the base to the vertex is at
View SolutionThe curved surface area of a cone is 12320cm2. If the radius of its base is 56 cm, find its height.
View SolutionFind the curved surface area of a cone, if its slant height is 60cm and the radius of its base is 21cm.
View SolutionFind the total surface area of a cone, if its slant height is 9m and the radius of its base is 12m.
View SolutionThe height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base.
View SolutionThe height of a cone is 15cm. If its volume is 500π cm3 , then find the radius of its base.
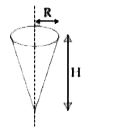
View SolutionShown in the figure is a hollow ice-cream cone (it is open at the top). If its mass is M, radius of its top , R and height , H, then its moment of inertia its axis is :
View Solution
