A unit positive point charge of mass m is projected with a velocity V inside the tunnel as shown. The tunnel has been made inside a uniformly charged nonconducting sphere. The minimum velocity with which the point charge should be projected such that it can reach the opposite end of the tunnel is equal to
(##BMS_V03_C03_E01_124_Q01.png" width="80%">
[ρR24mε0]1/2
[ρR224mε0]1/2
[ρR26mε0]1/2
zero because the initial and the final points are at same potential
The correct Answer is:A
KQR+12mu2=KQ2R3(3R2−R24)+0
14π∈0R×ρ×43πR3+12mu2=11×ρ×43πR38×2R2
∴u=[ρR24m∈0]1/2
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-04
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
19 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
The minimum velocity v with which charge q should be projected so that it manages to reach the centre of the ring starting from the position shown in figure is
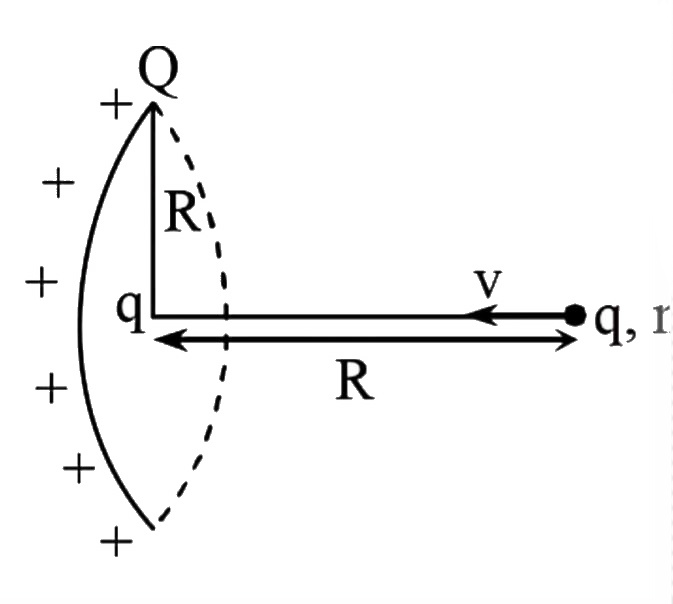
View SolutionFind the effective resistance between points A and B for the network shown in the figure below.
(ARH_NEET_PHY_OBJ_V02_C03_S01_027_Q01.png" width="80%">
View SolutionA charge +Q is uniformly distributed in a spherical volume of radius R. A particle of charge +q and mass m projected with velocity v0 the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of v0 such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is
View SolutionA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
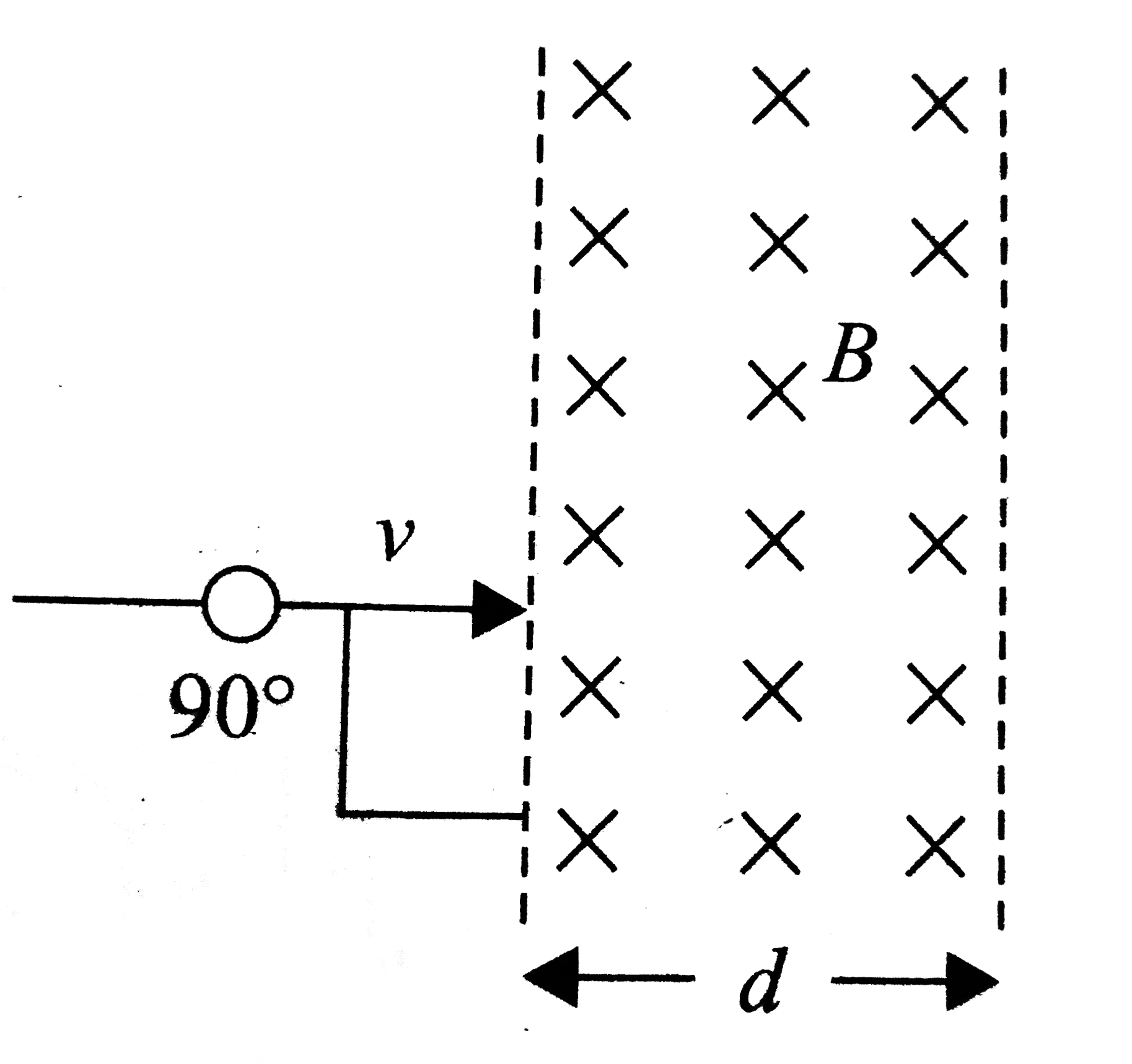
View SolutionA charge particle of mass m and charge q is projected with velocity v along plane a distance a from a long straight current carrying conductor as shown in figure. The radius of curvature of the path traced by the particle at the given position does not depend on

View SolutionA positive charge q of mass m is projected , a very large distance , toward a fixed non-conducting sphere having Q charge uniformly distributed inside it, as shown in figure. If the charge q just grazes the sphere , then the speed of projection u is κ=(14πε0).
_PHY_E01_008_Q01.png)
View SolutionA charged particle having charge 2q and mass m is projected from origin in X-Y plane with a velocity v inclined at an angle of 45∘ with positive X-axis in a region where a uniform magnetic field B unit exists along +z axis. The coordinates of the centre of the circular path of the particle are
View Solution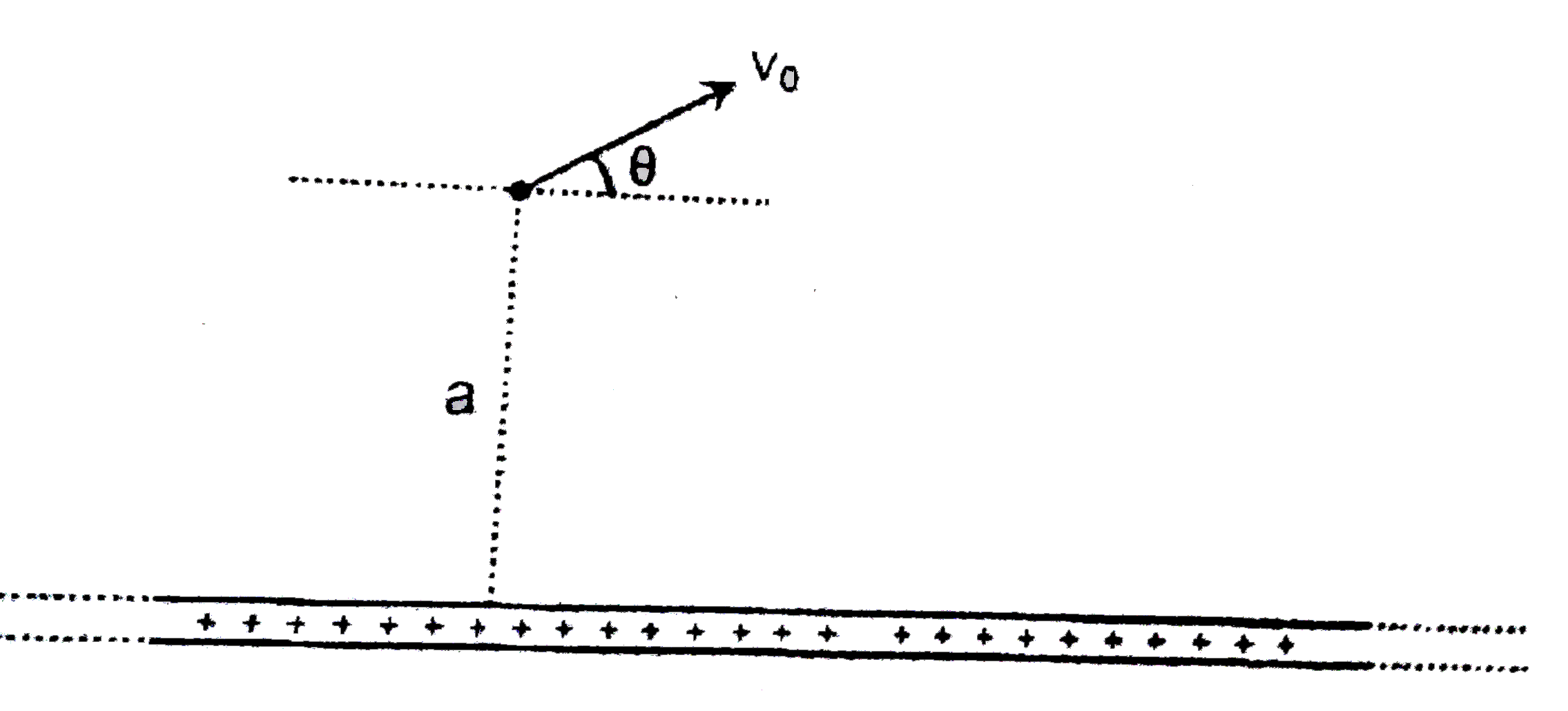
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε20/qλ). The value of n is (ingnore gravity)
View Solution
A hollow sphere of mass m and radius R is placed on smooth gound. A particle of mass m is projected with velocity v0 and angle θ lowest point a inside the sphere as shown in diagram if particle strikes the sphere at a point which is on horizontal level of centre and at that moment particle is at highest point. The collision between particle and sphere is elastic. The value of v0 is
View SolutionA positive charge +Q is fixed at a point A. Another positively charged particle of mass m and charge +q is projected from a point B with velocity u as shown in (Fig. 3.103). Point B is at a large distance from A and at distance d from the line A C. The initial velocity is parallel to the line A C. The point C is at a very large distance from A. Find the minimum distance (in meter) of +q from +Q during the motion. Take Qq=4πε0mu2d and d(√2−1)m.
 .
.
View Solution
