A charged particle having charge 2q and mass m is projected from origin in X-Y plane with a velocity v inclined at an angle of 45∘ with positive X-axis in a region where a uniform magnetic field B unit exists along +z axis. The coordinates of the centre of the circular path of the particle are
(0,0,0)
(−mv√2qB,mv√2qB,0)
(−√2mvqB,√2mvqB,0)
none of the above
The correct Answer is:D
To solve the problem, we need to find the coordinates of the center of the circular path of a charged particle projected in a magnetic field. Let's go through the solution step by step.
Step 1: Understand the scenario
We have a charged particle with charge 2q and mass m projected from the origin (0,0) in the XY plane with a velocity v at an angle of 45∘ with the positive X-axis. A uniform magnetic field B exists along the +Z axis.
Step 2: Determine the magnetic force
The magnetic force acting on the charged particle is given by the Lorentz force equation:
F=q(v×B)
For our case, substituting q=2q:
F=2q(v×B)
Since the magnetic field is along the +Z direction, we can denote it as B=B^k.
Step 3: Calculate the velocity components
The velocity v can be broken down into its components:
- vx=vcos(45∘)=v√2
- vy=vsin(45∘)=v√2
Step 4: Calculate the magnetic force
Using the right-hand rule and the cross product, the force will be directed towards the center of the circular path. The magnitude of the magnetic force is:
F=2q⋅v⋅B
Step 5: Set up the centripetal force equation
For circular motion, the magnetic force provides the necessary centripetal force:
Fc=mv2r
Setting the magnetic force equal to the centripetal force:
2qvB=mv2r
Step 6: Solve for the radius r
Rearranging the equation gives us:
r=mv2qB
Step 7: Find the coordinates of the center of the circular path
The center of the circular path will be offset from the origin. Since the particle moves in a circular path, the center will lie along the line that bisects the angle of projection. The coordinates of the center can be determined using trigonometric functions:
- The x-coordinate of the center will be rcos(45∘)
- The y-coordinate of the center will be rsin(45∘)
Substituting r:
x=rcos(45∘)=mv2qB⋅1√2=mv2qB√2
y=rsin(45∘)=mv2qB⋅1√2=mv2qB√2
Since the particle is moving in the negative y-direction, we take the y-coordinate as negative:
y=−mv2qB√2
Final Answer
Thus, the coordinates of the center of the circular path are:
(mv2qB√2,−mv2qB√2,0)
We have a charged particle with charge 2q and mass m projected from the origin (0,0) in the XY plane with a velocity v at an angle of 45∘ with the positive X-axis. A uniform magnetic field B exists along the +Z axis.
The magnetic force acting on the charged particle is given by the Lorentz force equation:
F=q(v×B)
For our case, substituting q=2q:
F=2q(v×B)
Since the magnetic field is along the +Z direction, we can denote it as B=B^k.
The velocity v can be broken down into its components:
- vx=vcos(45∘)=v√2
- vy=vsin(45∘)=v√2
Using the right-hand rule and the cross product, the force will be directed towards the center of the circular path. The magnitude of the magnetic force is:
F=2q⋅v⋅B
For circular motion, the magnetic force provides the necessary centripetal force:
Fc=mv2r
Setting the magnetic force equal to the centripetal force:
2qvB=mv2r
Rearranging the equation gives us:
r=mv2qB
The center of the circular path will be offset from the origin. Since the particle moves in a circular path, the center will lie along the line that bisects the angle of projection. The coordinates of the center can be determined using trigonometric functions:
- The x-coordinate of the center will be rcos(45∘)
- The y-coordinate of the center will be rsin(45∘)
x=rcos(45∘)=mv2qB⋅1√2=mv2qB√2
y=rsin(45∘)=mv2qB⋅1√2=mv2qB√2
y=−mv2qB√2
Thus, the coordinates of the center of the circular path are:
(mv2qB√2,−mv2qB√2,0)
Similar Questions
A moving charged particle q travelling along the positive X-axis enters a uniform magnetic field B. When will the force acting on q be maximum?
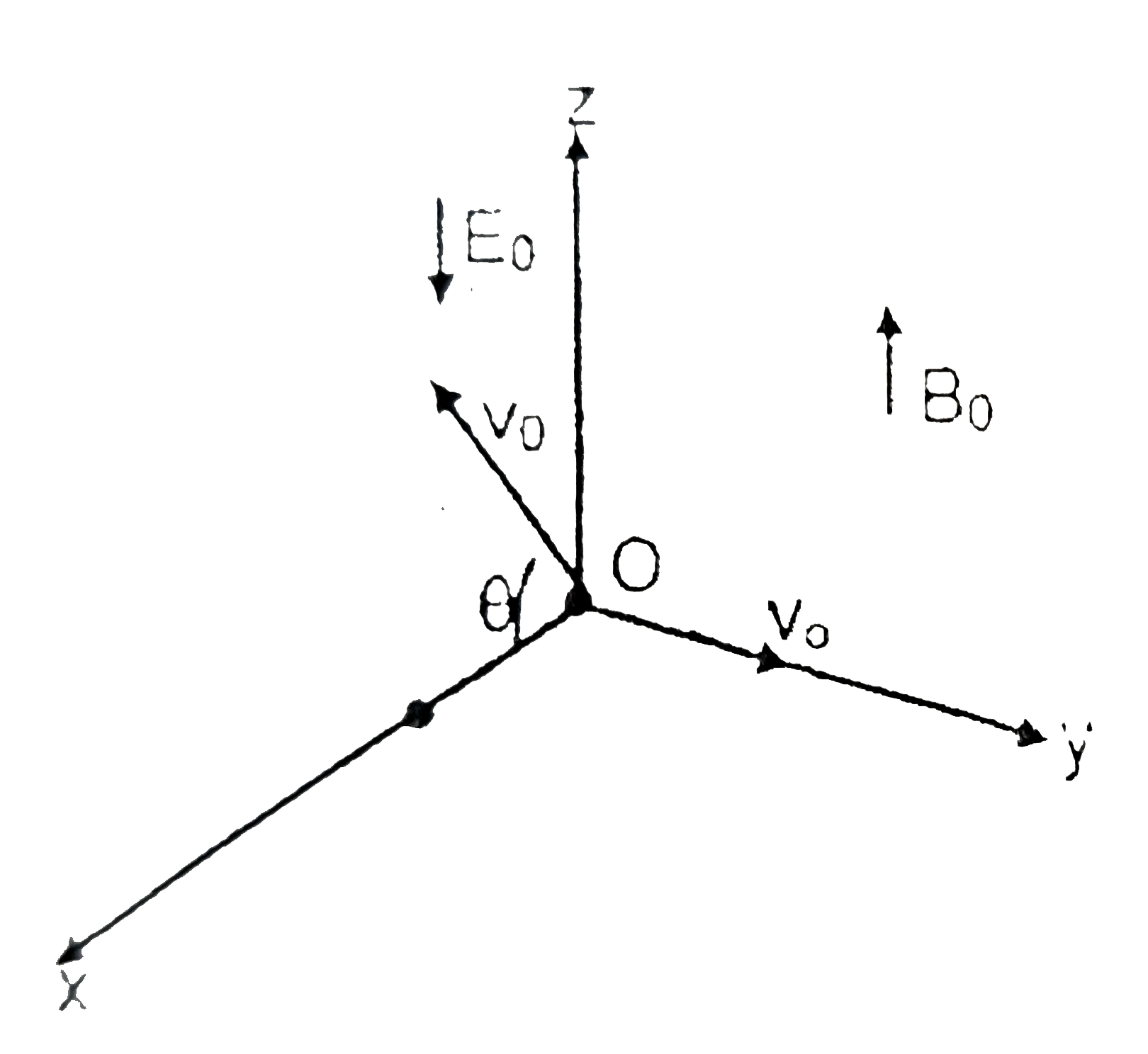
View SolutionA charged point particle having positive charge q, mass m is projected in x−z plane with a speed v0 at an angle θ with the x−axis , while another identical particle is projected simultaneously along the y−axis from the origin (see figure) with an equal speed v0.
An electric field →E=−E0ˆk exists in the x−z plane, while a magnetic field →B=B0ˆk exists in the region y>0 (F0, B0>0). It is observed that both the particles collide after some time. Assume that the space is gravity free.
(i) Find the time after which the particles collide and the coordinates of the point of collision.
(ii) Find the velocity v0 and the angle θ in terms of the other variables.
(iii) What is the maximum value of the z− coordinate of the first particle ?
View SolutionAn electron is projected along positive z-axis, magnetic field is present along y-axis then direction of initial acceleration of the particle is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic field of strength B is also switched on along positive y-axis.
Velocity of the particle just before the magnetic field is switched on is
View SolutionA charge q of mass m is moving with a velocity of V, at right angles to a uniform magnetic field B. Deduce the expression for the radius of the circular path it describes.
View SolutionA particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View SolutionA particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA charged particle enters in a magnetic field B with its initial velocity making an angle of 45° with B. The path of the particle will be
View Solution
