Statement-1 : If two concentric conducing sphere which are connected by a conducting wire. No charge can exist on inner sphere.
Statement-2: When charge on outer sphere will exist then potential of inner shell and outer shell will be same.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation of statement 1
Statement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation of statement 1
Statement-1 is False, Statement-2 is True
Statement-1 is True, Statement-2 is False.
The correct Answer is:D
To solve the question, we need to analyze both statements regarding the behavior of two concentric conducting spheres connected by a conducting wire.
Step 1: Analyze Statement 1
- Statement 1 claims that if two concentric conducting spheres are connected by a conducting wire, no charge can exist on the inner sphere.
- According to the properties of conductors, the electric field inside a conductor in electrostatic equilibrium is zero. This implies that any excess charge resides on the surface of the conductor.
- Since the inner sphere is connected to the outer sphere via a conducting wire, any charge that might be present on the inner sphere would redistribute to the outer sphere. Therefore, the inner sphere cannot hold any charge.
- Conclusion: Statement 1 is true.
Step 2: Analyze Statement 2
- Statement 2 states that when charge exists on the outer sphere, the potential of the inner shell and the outer shell will be the same.
- The potential inside a conductor is constant and equal to the potential on its surface. Since the inner sphere has no charge, its potential is constant and equal to zero (assuming it is uncharged).
- The outer sphere, when charged, will have a potential that depends on its charge and radius. The potential at a point outside a charged sphere is given by V=kQr, where Q is the charge on the outer sphere and r is the distance from the center.
- Since the outer sphere has charge, its potential will not be zero and will differ from the potential of the inner sphere.
- Conclusion: Statement 2 is false.
Final Conclusion:
- Statement 1 is true, and Statement 2 is false.
- Statement 1 claims that if two concentric conducting spheres are connected by a conducting wire, no charge can exist on the inner sphere.
- According to the properties of conductors, the electric field inside a conductor in electrostatic equilibrium is zero. This implies that any excess charge resides on the surface of the conductor.
- Since the inner sphere is connected to the outer sphere via a conducting wire, any charge that might be present on the inner sphere would redistribute to the outer sphere. Therefore, the inner sphere cannot hold any charge.
- Conclusion: Statement 1 is true.
- Statement 2 states that when charge exists on the outer sphere, the potential of the inner shell and the outer shell will be the same.
- The potential inside a conductor is constant and equal to the potential on its surface. Since the inner sphere has no charge, its potential is constant and equal to zero (assuming it is uncharged).
- The outer sphere, when charged, will have a potential that depends on its charge and radius. The potential at a point outside a charged sphere is given by V=kQr, where Q is the charge on the outer sphere and r is the distance from the center.
- Since the outer sphere has charge, its potential will not be zero and will differ from the potential of the inner sphere.
- Conclusion: Statement 2 is false.
- Statement 1 is true, and Statement 2 is false.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 1
5 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 2
8 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-03
7 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
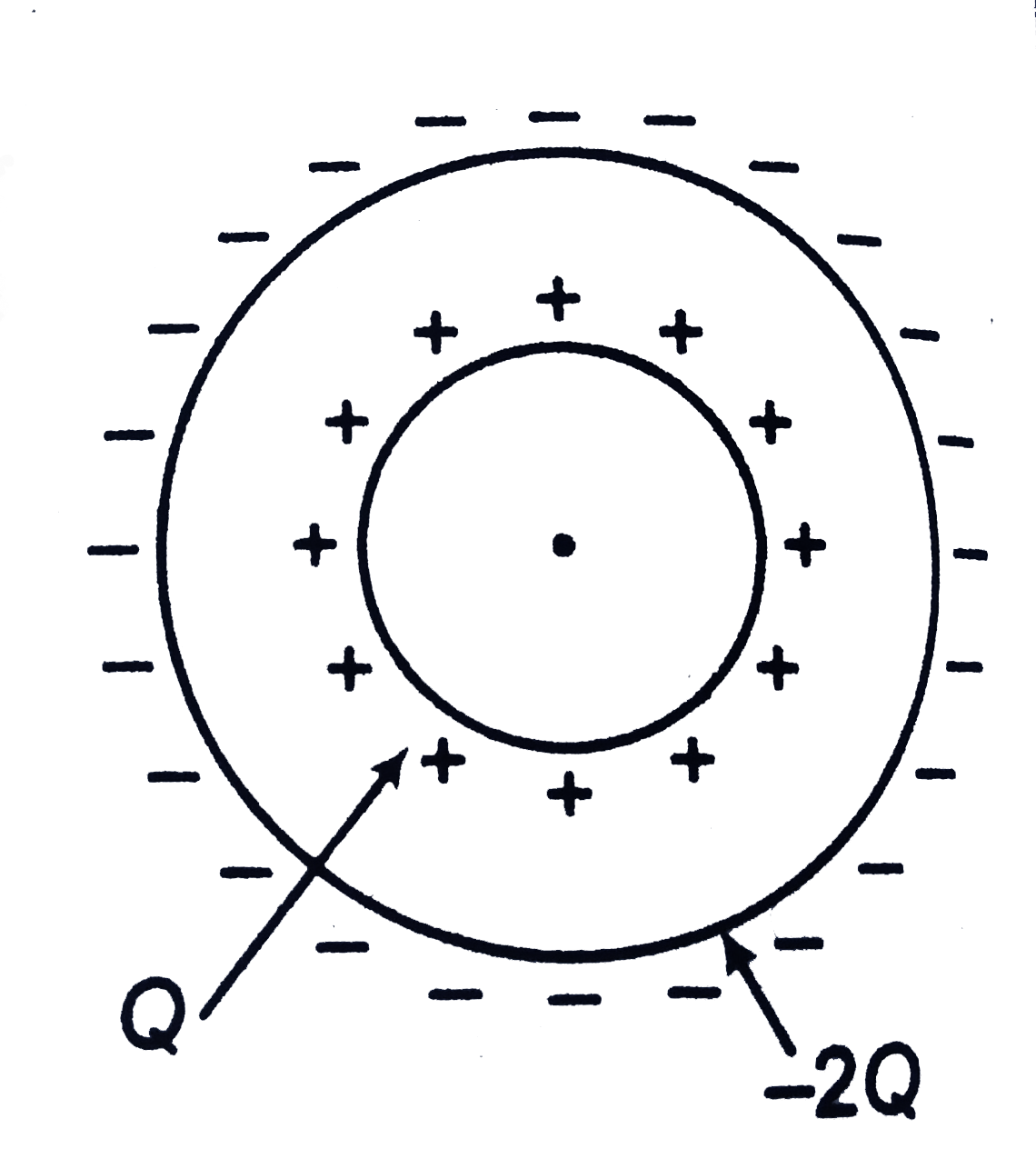
Two concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
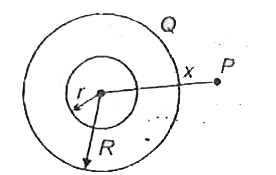
View SolutionTwo concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
View SolutionThere are two concentric conducting spherical shells of radii 10cm and 20cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionThree concentric conducting sphereical shells carry charges +4Q on the inner shell −2Q on the middle shel and +6Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionThere are three concentric conducting spherical shells. All of them are charged. The innermost sphere is connected by a conducting wire to the outermost sphere. Prove that the final charge on the innermost sphere is independent of the initial charge of outermost sphere.
View SolutionIf the electric potential of the inner metal sphere is 10 volt & that of the outer shell is 5 volt then the potential at the centre will be
View SolutionThere are two concentric conducting shells. The potential of outer shell is 10 V and that of inner shell is 15 V. If the outer shell is grounded, the potential of iner shell becomes / remains.
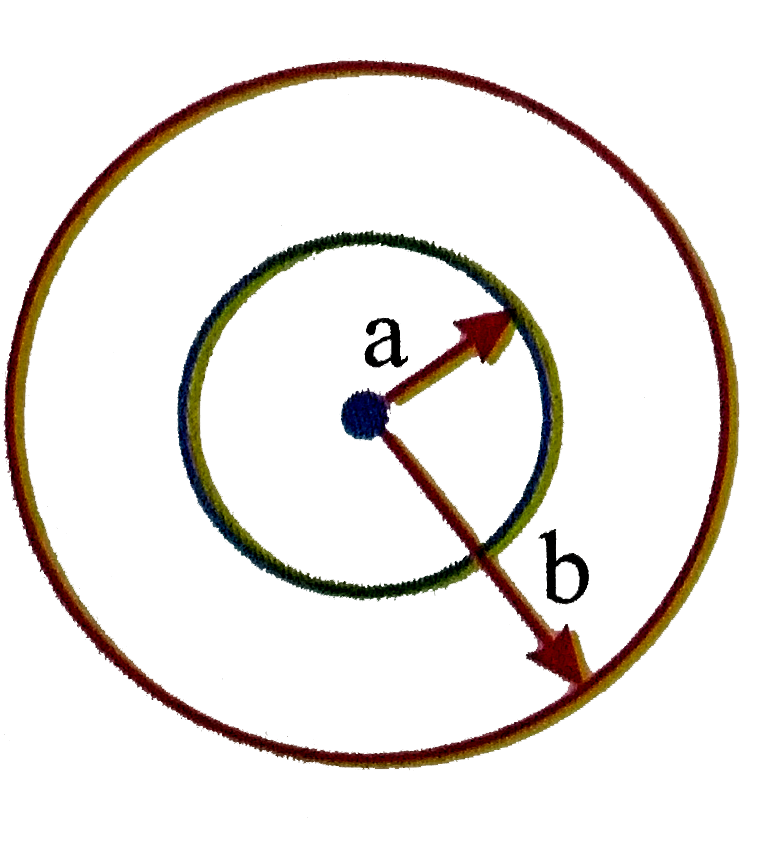
View SolutionA and B are two thin concentric hollow conductors having radii a and 2a and charge 2Q and Q, respectively. If potential of outer sphere is 5V, then potential of inner sphere is
View SolutionThree concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionIn (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View Solution
