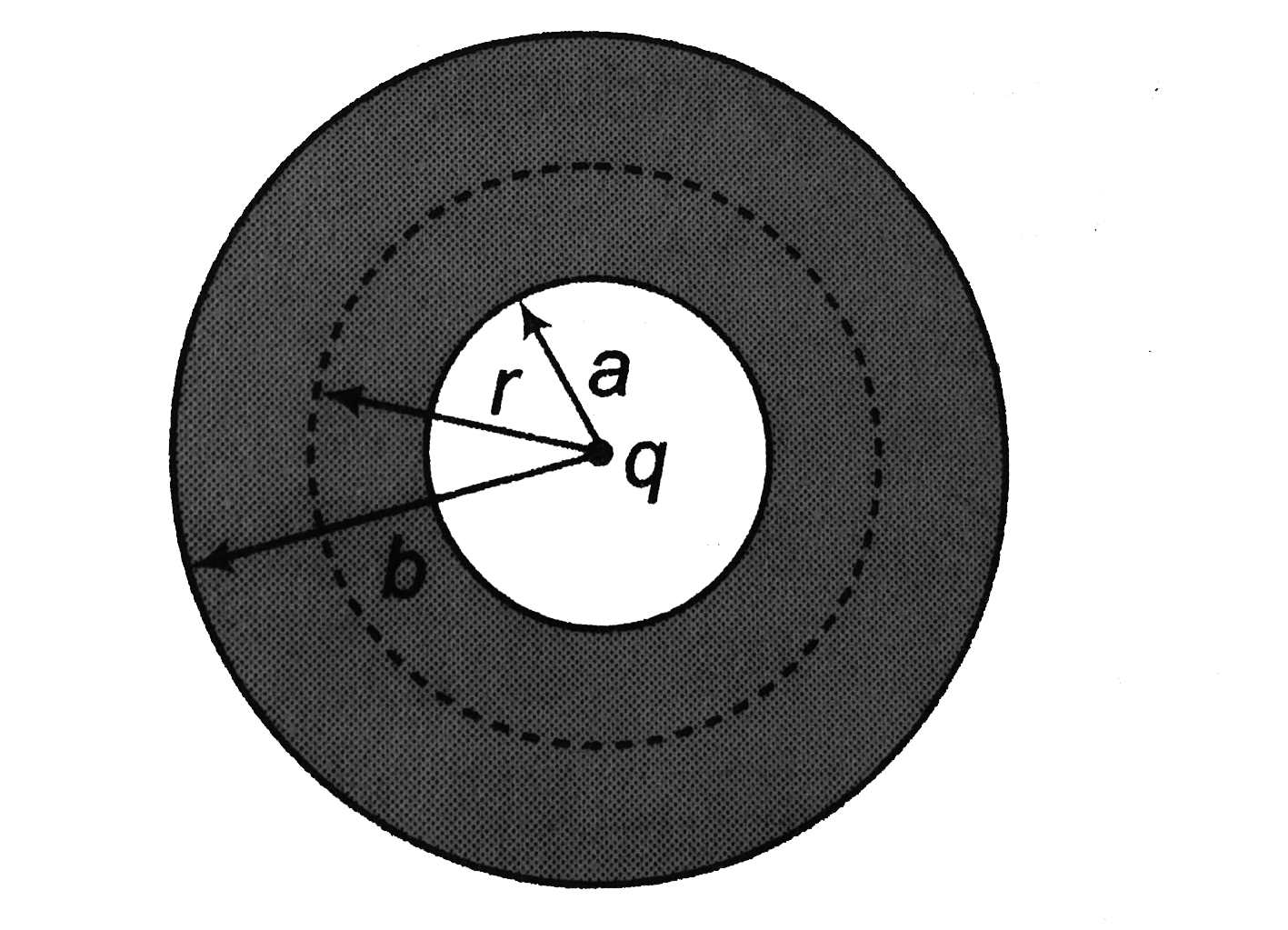
The region between two concentric spheres of radii a and b (gt a) contains volume charge The I where C is a constant and r is the radial distance as shown in figure. A point dens') barge q is placed at the origin, r=0. c find the value of C for which the electric field in the region between the spheres is constant (i.e. r independent).
2Qπa2
Q2πa2
Q2π(b2−a2)
2Qπ(a2−b2)
The correct Answer is:B
Gaussian surface at distance r from center
Q+r∫aAr4πr2dr∈0=E4πr2
E=Q+2πAr2−2πAa24πr2∈0
make E independent of r then
Q−2πa2A=0⇒A=Q2πa2

Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)
19 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - MCQ s WITH ONE OR MORE THAN ONE CORRECT ANSWER
6 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[B]
16 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
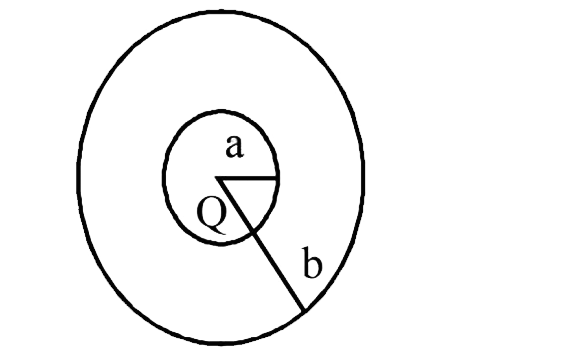
View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density p=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
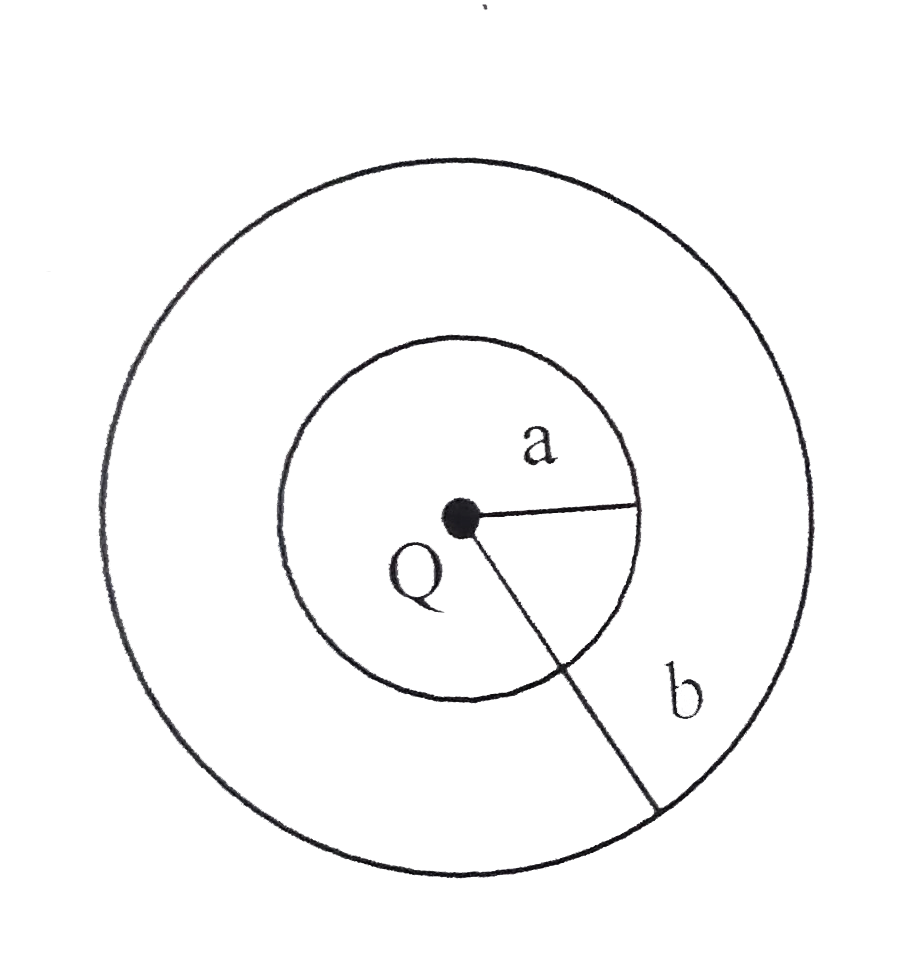
View Solution
Knowledge Check
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
Two charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
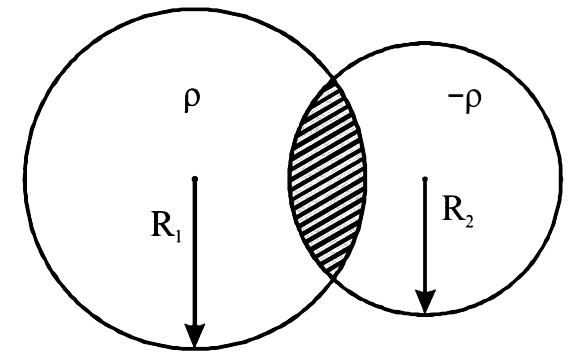
View SolutionTwo non-conducting spheres of radii R1 and R2 and carrying uniform volume charge densities +ρ and −ρ, respectively, are placed such that they partially overlap, as shown in the figure. At all points in the overlapping region
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and R(>r) such that the surface charge densities are equal. Find the potential at the common centre.
View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and R(>r) such that the surface charge densities are equal. Find the potential at the common centre.
View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and R(>r) such that the surface charge densities are equal. Find the potential at the common centre.
View SolutionIn a spherical distribution , the charge density varies as ρ(r)=A/r for a<r<b (as shown) where A is constant . A point charge Q lies at the centre of the sphere at r = 0 . The electric filed in the region a<r<b has a constant magnitude for
View Solution
