A bead is arranged to move with constant speed around a loop that lies in a vetical plane. The magnitude of the net force on the bead is
maximum at the bottom
maximum at the top
maximum at the side points
the same at all points
The correct Answer is:A
To determine the magnitude of the net force on a bead moving with constant speed around a vertical loop, we can analyze the forces acting on the bead at different points in the loop.
1. Understand the Forces Acting on the Bead:
- The bead experiences two main forces: the gravitational force (weight) acting downward, mg, where m is the mass of the bead and g is the acceleration due to gravity, and the normal force N exerted by the track on the bead.
2. Analyze the Bead at Different Points:
- We will analyze the forces at three key points: the bottom of the loop, the top of the loop, and a point on the side (horizontal position).
3. At the Bottom of the Loop:
- At this position, the net force towards the center (centripetal force) is given by:
N1−mg=mv2R
Rearranging gives:
N1=mg+mv2R
- Here, N1 is the normal force at the bottom, which is the maximum force experienced by the bead.
4. At the Top of the Loop:
- At the top, the forces acting on the bead are:
N2+mg=mv2R
Rearranging gives:
N2=mv2R−mg
- Here, N2 is the normal force at the top, which is the minimum force experienced by the bead.
5. At the Horizontal Position:
- At this position, the forces are:
N3=mv2R
- Here, N3 is the normal force at the horizontal position.
6. Comparison of Forces:
- From the equations derived:
- At the bottom: N1=mg+mv2R (maximum)
- At the top: N2=mv2R−mg (minimum)
- At the horizontal position: N3=mv2R
7. Conclusion:
- The magnitude of the net force on the bead is maximum at the bottom of the loop, where it is given by:
N1=mg+mv2R
Final Answer:
The magnitude of the net force on the bead is maximum at the bottom of the loop, given by N1=mg+mv2R.
- The bead experiences two main forces: the gravitational force (weight) acting downward, mg, where m is the mass of the bead and g is the acceleration due to gravity, and the normal force N exerted by the track on the bead.
- We will analyze the forces at three key points: the bottom of the loop, the top of the loop, and a point on the side (horizontal position).
- At this position, the net force towards the center (centripetal force) is given by:
N1−mg=mv2R
Rearranging gives:
N1=mg+mv2R
- Here, N1 is the normal force at the bottom, which is the maximum force experienced by the bead.
- At the top, the forces acting on the bead are:
N2+mg=mv2R
Rearranging gives:
N2=mv2R−mg
- Here, N2 is the normal force at the top, which is the minimum force experienced by the bead.
- At this position, the forces are:
N3=mv2R
- Here, N3 is the normal force at the horizontal position.
- From the equations derived:
- At the bottom: N1=mg+mv2R (maximum)
- At the top: N2=mv2R−mg (minimum)
- At the horizontal position: N3=mv2R
- The magnitude of the net force on the bead is maximum at the bottom of the loop, where it is given by:
N1=mg+mv2R
The magnitude of the net force on the bead is maximum at the bottom of the loop, given by N1=mg+mv2R.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is

View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration

A. the normal reaction on the bead will be constant h magnitude and direction both
B. the magnitude of the normal reaction on the bead will be variable
C. the magnitude of friction force on the bead will be constant
D. the magnitude of friction force on the bead will be variable
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r. Find magnitude of average force on it in half revolution.
View SolutionAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
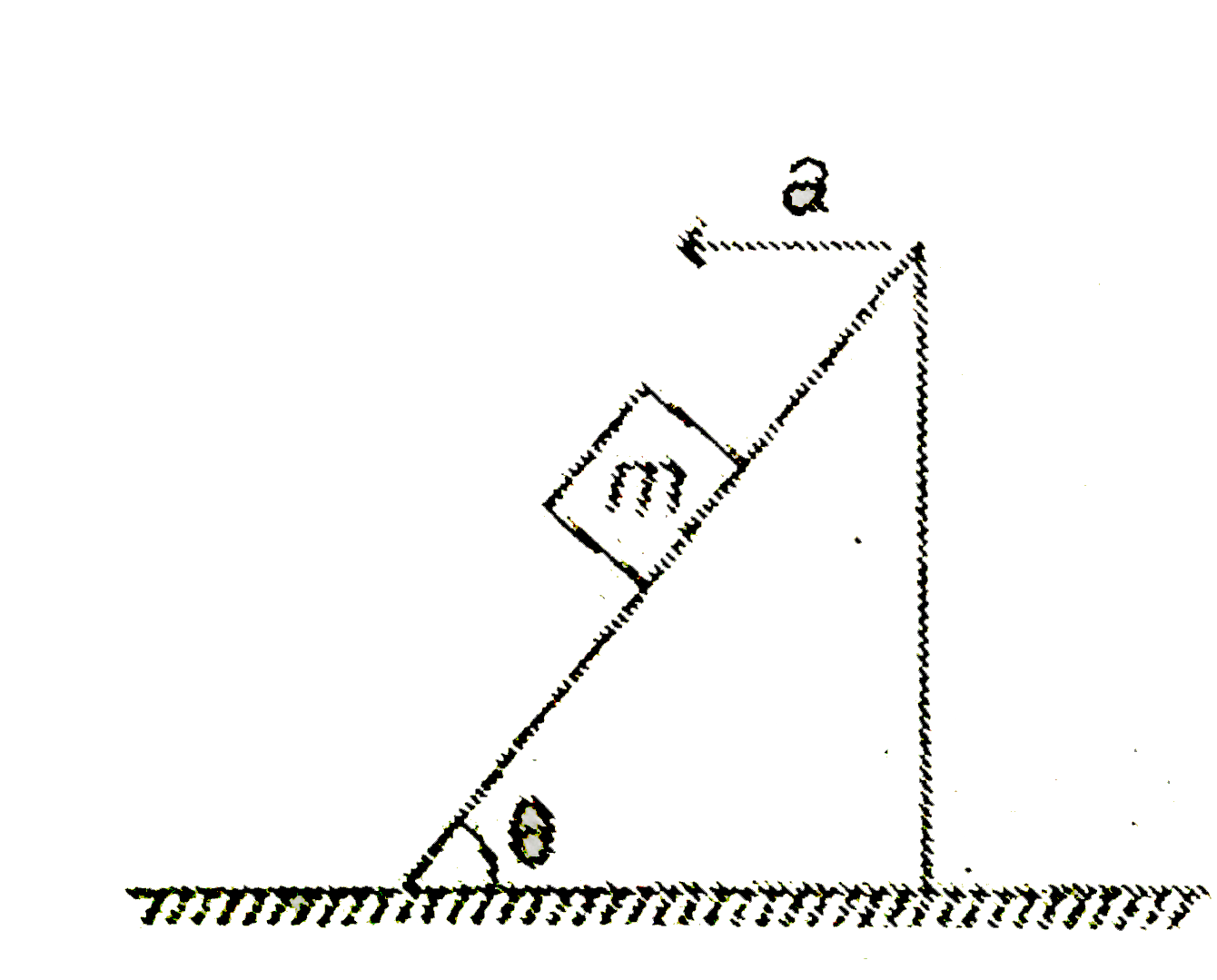
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
View SolutionA circular loop of radius 20 cm carries a current of 10 A. An electron crosses the plane of the loop with a speed of ( 2.0 xx (10^6) m s^-1). The direction of motion makes an angle of 30^@ with the axis of the circle and passes through its centre. Find the magnitude of the magnetic force on the electron at the instant it crosses the plane.
View SolutionA car is moving along a circle with constant speed on an inclined plane as shown in diagram. Then friction force on car will be in horizontal direction at least at one point :

View SolutionWhy is the motion of a body moving with a constant speed around a circular path said to be accelerated ?
View SolutionAn object of mass 5 kg moves at a constant speed of 6 m/s in a circular path of radius 2m. Find the magnitude of the object's acceleration and the net force responsible for its motion.
View SolutionA particle is moving along a circular path with a constant speed 10ms−1.What is the magnitude of the change in velocity of the particle ,when it moves through an angle of 60∘ around the center of the circle ?
View Solution
