A man of mass stands on a plank of mass . The plank is lying on a smooth horizontal floor. Initianlly both are at rest. The man starts walking on the plank towards north and stops after moving a distance of on the plank. Then
The center of mas os plank man system remains stationary.
The plank will slide to the north by a distance 6m
The plank will slide to the south by a distance 6m
The plank will slids to the south by a distance 12m
The correct Answer is:A
To solve the problem, we need to analyze the situation using the principles of conservation of momentum and the concept of the center of mass. Here’s a step-by-step solution:
Step 1: Understand the System
We have a man of mass m1=80kg standing on a plank of mass m2=40kg. Initially, both the man and the plank are at rest.
Step 2: Define the Displacements
When the man walks a distance of dm=6m towards the north on the plank, the plank will move a distance dp in the opposite direction (south) due to the conservation of momentum.
Step 3: Apply Conservation of Momentum
Since there are no external horizontal forces acting on the system, the center of mass of the system must remain stationary. Therefore, the total momentum before and after the man starts walking must be equal.
Let dp be the distance the plank moves south. The displacement of the man with respect to the ground can be expressed as:
dman,ground=dm−dp
Step 4: Calculate the Center of Mass
The position of the center of mass xcm of the system can be calculated using the formula:
xcm=m1⋅x1+m2⋅x2m1+m2
where x1 is the position of the man and x2 is the position of the plank.
Since the initial center of mass is at rest, we can set up the equation:
m1⋅(dm−dp)+m2⋅(−dp)=0
Step 5: Substitute Values
Substituting the values we have:
80⋅(6−dp)+40⋅(−dp)=0
Expanding this gives:
480−80dp−40dp=0
Combining like terms:
480−120dp=0
Step 6: Solve for dp
Now, solving for dp:
120dp=480
dp=480120=4m
Conclusion
The plank moves south by a distance of 4m while the man walks 6m north on the plank. Thus, the center of mass of the system remains stationary.
Final Answer
The plank moves south by 4m.
We have a man of mass m1=80kg standing on a plank of mass m2=40kg. Initially, both the man and the plank are at rest.
When the man walks a distance of dm=6m towards the north on the plank, the plank will move a distance dp in the opposite direction (south) due to the conservation of momentum.
Since there are no external horizontal forces acting on the system, the center of mass of the system must remain stationary. Therefore, the total momentum before and after the man starts walking must be equal.
dman,ground=dm−dp
The position of the center of mass xcm of the system can be calculated using the formula:
xcm=m1⋅x1+m2⋅x2m1+m2
where x1 is the position of the man and x2 is the position of the plank.
m1⋅(dm−dp)+m2⋅(−dp)=0
Substituting the values we have:
80⋅(6−dp)+40⋅(−dp)=0
Expanding this gives:
480−80dp−40dp=0
Combining like terms:
480−120dp=0
Now, solving for dp:
120dp=480
dp=480120=4m
The plank moves south by a distance of 4m while the man walks 6m north on the plank. Thus, the center of mass of the system remains stationary.
The plank moves south by 4m.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A man of mass 50kg us standing on a 100kg plank kept on a fricitonless horizontal floor. Initially both are at rest. If the man starts walking on the plank with speed 6m/s towards right relative to the plank, then amount of muscle energy spent by the man is
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionA man of mass 60 kg is standing on a boat of mass 140 kg, which is at rest in still water. The man is initially at 20 m from the shore. He starts walking on the boat for 4 s with constant speed 1.5 m/s towards the shore. The final distance of the man from the shore is
View SolutionA man of mass m is moving with a constant acceleration a w.r.t. plank. The plank lies on a smooth horizontal floor. If mass of plank is also m then the frictional force exerted by plank on man is ma/k. Find the value of k.
View SolutionA man of mass m is standing at one end of a trolley of mass Mand length L placed at rest on a smooth horizontal surface. The man starts moving towards the other end and covers distance L, then distance moved by man w.r.t ground is
View SolutionA wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA uniform wooden plank of mass 150 kg and length 8 m is floating on still water with a man of 50 kg at one end of it . The man walks to the other end of the plank and stops. Than the distance covered by the plank is
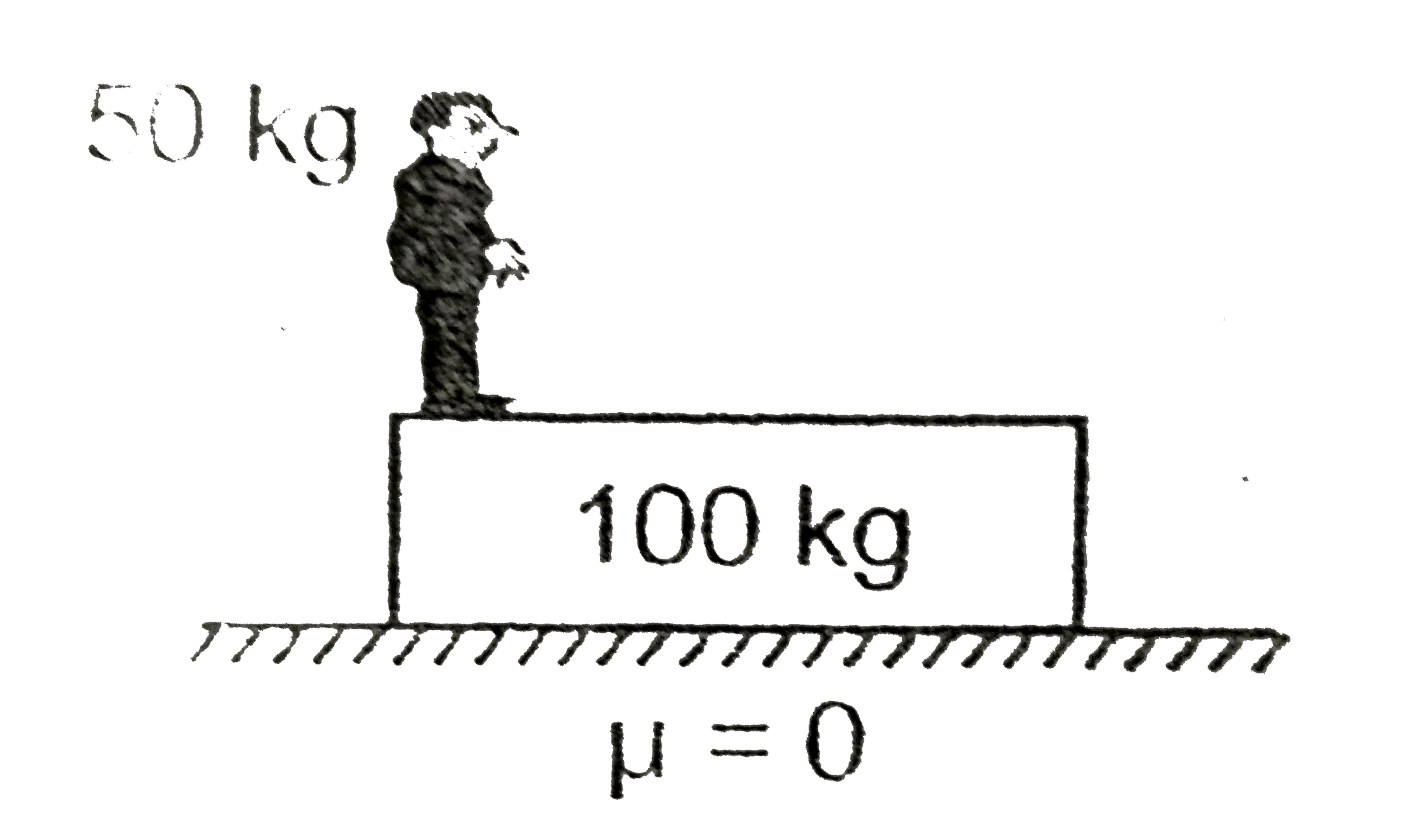
View SolutionA man of mass 50 kg is pulling on a plank of mass 100 kg kept on a smooth floor as shown with force of 100 N. If both man & plank move together, find force of friction acting on man.

View SolutionThree man A, B & C of mass 40kg,50kg & 60kg are standing on a plank of mass 90kg, which is kept on a smooth horizontal plane. If A & C exchange their position then mass B will shift :-

View SolutionA man of mass m is standing at one end of of a plank of mass M. The length of the plank is L and it rests on a frictionless horizontal ground. The man walks to the other end of the plank. Find displacement of the plank and man relative to the ground.

View Solution
