The angular speed of a star spinning about its axis increases as the star begins to contract to a smaller radius. Which of the following quantities associated with the star must decrease as this occurs?
Moment of inertia
Angular momentum
Rotational kinetic energy
Net external torque
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the angular momentum, moment of inertia, angular speed, and rotational kinetic energy of the star as it contracts.
1. Understanding Angular Momentum:
The angular momentum L of a rotating object is given by the formula:
L=Iω
where I is the moment of inertia and ω is the angular speed.
2. No External Torque:
The problem states that there is no external torque acting on the star. This means that the angular momentum L remains constant:
dLdt=0⟹L=constant
3. Moment of Inertia and Angular Speed:
As the star contracts, its radius decreases, which leads to a decrease in the moment of inertia I. The moment of inertia for a solid sphere, for example, is given by:
I=25mr2
where m is the mass and r is the radius. As r decreases, I decreases.
4. Relationship Between Angular Speed and Moment of Inertia:
Since L is constant and I is decreasing, we can see that ω must increase to keep the product Iω constant:
L=Iω⟹If I decreases, then ω must increase.
5. Rotational Kinetic Energy:
The rotational kinetic energy K is given by:
K=12Iω2
Since I is decreasing and ω is increasing, we need to analyze how these changes affect K.
6. Analyzing the Kinetic Energy:
We can express ω in terms of L:
ω=LI
Substituting this into the kinetic energy formula gives:
K=12I(LI)2=L22I
Since I is decreasing, K must increase because L is constant.
7. Conclusion:
The only quantity that must decrease as the star contracts and angular speed increases is the moment of inertia I.
Final Answer:
The quantity that must decrease as the star contracts is the moment of inertia (I).
The angular momentum L of a rotating object is given by the formula:
L=Iω
where I is the moment of inertia and ω is the angular speed.
The problem states that there is no external torque acting on the star. This means that the angular momentum L remains constant:
dLdt=0⟹L=constant
As the star contracts, its radius decreases, which leads to a decrease in the moment of inertia I. The moment of inertia for a solid sphere, for example, is given by:
I=25mr2
where m is the mass and r is the radius. As r decreases, I decreases.
Since L is constant and I is decreasing, we can see that ω must increase to keep the product Iω constant:
L=Iω⟹If I decreases, then ω must increase.
The rotational kinetic energy K is given by:
K=12Iω2
Since I is decreasing and ω is increasing, we need to analyze how these changes affect K.
We can express ω in terms of L:
ω=LI
Substituting this into the kinetic energy formula gives:
K=12I(LI)2=L22I
Since I is decreasing, K must increase because L is constant.
The only quantity that must decrease as the star contracts and angular speed increases is the moment of inertia I.
The quantity that must decrease as the star contracts is the moment of inertia (I).
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
The angular speed of rotation of earth about its axis at which the weight of man standing on the equator becomes half of his weight at the poles is given by
View SolutionA constant current I is maintained in a solenoid. Which of lthe following quantities will increase if an iron rod is inserted in the solenoid along its axis?
View Solution
Knowledge Check
Comprehension given below is followed by some multiple choice question, Each question has one correct options. Choose the correct option.
Molecular orbitals are formed by the overlap of atomic orbitals. Two atomic orbitals combine to form two molecular orbitals called bonding molecular orbital (BMO) and anti-bonding molecular orbital (ABMO). Energy of anti-bonding orbital is raised above the parent atomic orbitals that have combined and hte energy of the bonding orbital is lowered than the parent atomic orbitals.
energies of various molecular orbitals for elements hydrogen to nitrogen increase in the order
σ1s<σ⋆1s<σ⋆2s<((π2px)=(π2py))<σ2pz<(π⋆2px=π⋆2py)<σ⋆2pz and For oxygen and fluorine order of enregy of molecules orbitals is given below.
σ1s<σ⋆1s<σ2s<σ⋆2s<σpz<(π2px≈π2py)<(π⋆2px≈π⋆2py)<σ⋆2pz
Different atomic orbitalsof one atom combine with those atoms orbitals of the second atom which have comparable energies and proper orientation.
Further, if the overlapping is head on, the molecular orbital is called sigma, σ andif the overlap is lateral, the molecular orbital is called pi, π. The molecular orbitals are filled with electrons according to the same rules as followed for filling of atomic orbitals.
However, the order for filling is not the same for all molecules or their ions. Bond order is one of the most important parameters to compare the strength of bonds.
67) Which of the following pair is expected to have the same bond order?AC2BB2CO2DBe2
The angular speed of earth's rotation about its own axis is ω. When its angular speed is increased to n time its original angular speed, the acceleration due to gravity at the equator becomes zero. What is the value of n?
[R is the equatorial radius of the earth]
View SolutionA uniform rod of length l is being rotated in a horizontal plane with a constant angular speed about an axis passing through one of its ends. If the tension generated in the rod due to rotation is T(x) at a distance x from the axis. Then which of the following graphs depicts it most closely?
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular speed 100s−1. The radius of the cylinder is 0.25m. What is the kinetic energy associated with the rotation of the cylinder ? What is the magnitude of angular momentum of the cylinder about its axis ?
View SolutionComprehension given below is followed by some multiple choice question, Each question has one correct options. Choose the correct option.
Molecular orbitals are formed by the overlap of atomic orbitals. Two atomic orbitals combine to form two molecular orbitals called bonding molecular orbital (BMO) and anti-bonding molecular orbital (ABMO). Energy of anti-bonding orbital is raised above the parent atomic orbitals that have combined and hte energy of the bonding orbital is lowered than the parent atomic orbitals.
energies of various molecular orbitals for elements hydrogen to nitrogen increase in the order
σ1s<σ⋆1s<σ⋆2s<((π2px)=(π2py))<σ2pz<(π⋆2px=π⋆2py)<σ⋆2pz and For oxygen and fluorine order of enregy of molecules orbitals is given below.
σ1s<σ⋆1s<σ2s<σ⋆2s<σpz<(π2px≈π2py)<(π⋆2px≈π⋆2py)<σ⋆2pz
Different atomic orbitalsof one atom combine with those atoms orbitals of the second atom which have comparable energies and proper orientation.
Further, if the overlapping is head on, the molecular orbital is called sigma, σ andif the overlap is lateral, the molecular orbital is called pi, π. The molecular orbitals are filled with electrons according to the same rules as followed for filling of atomic orbitals.
However, the order for filling is not the same for all molecules or their ions. Bond order is one of the most important parameters to compare the strength of bonds.
In which of the following molecules, σ2pz molecular orbital is filled after π2px and π2py molecular orbitals?
View SolutionComprehension given below is followed by some multiple choice question, Each question has one correct options. Choose the correct option.
Molecular orbitals are formed by the overlap of atomic orbitals. Two atomic orbitals combine to form two molecular orbitals called bonding molecular orbital (BMO) and anti-bonding molecular orbital (ABMO). Energy of anti-bonding orbital is raised above the parent atomic orbitals that have combined and hte energy of the bonding orbital is lowered than the parent atomic orbitals.
energies of various molecular orbitals for elements hydrogen to nitrogen increase in the order
σ1s<σ⋆1s<σ⋆2s<((π2px)=(π2py))<σ2pz<(π⋆2px=π⋆2py)<σ⋆2pz and For oxygen and fluorine order of enregy of molecules orbitals is given below.
σ1s<σ⋆1s<σ2s<σ⋆2s<σpz<(π2px≈π2py)<(π⋆2px≈π⋆2py)<σ⋆2pz
Different atomic orbitalsof one atom combine with those atoms orbitals of the second atom which have comparable energies and proper orientation.
Further, if the overlapping is head on, the molecular orbital is called sigma, σ andif the overlap is lateral, the molecular orbital is called pi, π. The molecular orbitals are filled with electrons according to the same rules as followed for filling of atomic orbitals.
However, the order for filling is not the same for all molecules or their ions. Bond order is one of the most important parameters to compare the strength of bonds.
67) Which of the following pair is expected to have the same bonod order?
View SolutionComprehension given below is followed by some multiple choice question, Each question has one correct options. Choose the correct option.
Molecular orbitals are formed by the overlap of atomic orbitals. Two atomic orbitals combine to form two molecular orbitals called bonding molecular orbital (BMO) and anti-bonding molecular orbital (ABMO). Energy of anti-bonding orbital is raised above the parent atomic orbitals that have combined and hte energy of the bonding orbital is lowered than the parent atomic orbitals.
energies of various molecular orbitals for elements hydrogen to nitrogen increase in the order
σ1s<σ⋆1s<σ⋆2s<((π2px)=(π2py))<σ2pz<(π⋆2px=π⋆2py)<σ⋆2pz and For oxygen and fluorine order of enregy of molecules orbitals is given below.
σ1s<σ⋆1s<σ2s<σ⋆2s<σpz<(π2px≈π2py)<(π⋆2px≈π⋆2py)<σ⋆2pz
Different atomic orbitalsof one atom combine with those atoms orbitals of the second atom which have comparable energies and proper orientation.
Further, if the overlapping is head on, the molecular orbital is called sigma, σ andif the overlap is lateral, the molecular orbital is called pi, π. The molecular orbitals are filled with electrons according to the same rules as followed for filling of atomic orbitals.
However, the order for filling is not the same for all molecules or their ions. Bond order is one of the most important parameters to compare the strength of bonds.
66) Which of the following moleculart orbitals has maximum number of nodal planes?
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
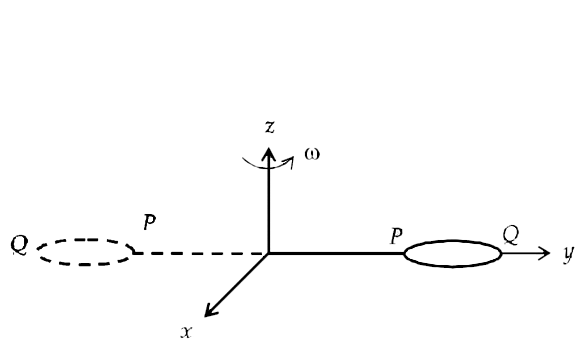
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
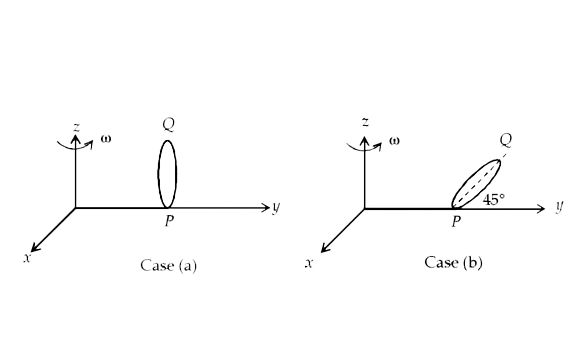
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View Solution
