STATEMENT-1: Two balls are dropped one after the other form a tall tower. The distance between them increases linearly with time (elapsed after the second ball is dropped and before the first hits ground).
STATEMENT-2: Relative acceleration is zero, whereas relative velocity non-zero in the above situation.
Statement-I is true, Statement-II is true, Statement-II is correct explanation for Statement-I
Statement-I is true, Statement-II is true, Statement-II is NOT a correct explanation for Statement-I
Statement-I is true, Statement-II is false
Statement-I is false, Statement-II is true.
The correct Answer is:A
To solve the problem, we will analyze the two statements given and derive the necessary conclusions step by step.
Step 1: Understanding the Problem
We have two balls dropped from a tall tower, one after the other. We need to analyze the distance between the two balls after the second ball is dropped and before the first ball hits the ground.
Step 2: Analyzing the Motion of the Balls
- Let the first ball be dropped at time t=0.
- The second ball is dropped at time t=t0 (let's say after a short interval).
- The first ball will have fallen a distance h1=12gt2 after time t.
- The second ball, dropped at t0, will fall a distance h2=12g(t−t0)2 after the same time t.
Step 3: Finding the Distance Between the Balls
The distance y between the two balls at time t after the second ball is dropped can be expressed as:
y=h1−h2
Substituting the expressions for h1 and h2:
y=12gt2−12g(t−t0)2
Expanding (t−t0)2:
y=12gt2−12g(t2−2tt0+t20)
Simplifying:
y=12g(2tt0−t20)
This shows that the distance y depends linearly on time t (since t is the variable).
Step 4: Analyzing Relative Velocity and Acceleration
- The acceleration of both balls is g (downward).
- The relative acceleration between the two balls is:
arel=a1−a2=g−g=0
- The relative velocity between the two balls can be calculated as:
vrel=v1−v2
Since both balls are accelerating downward, the relative velocity is non-zero.
Conclusion
- Statement 1: The distance between the two balls increases linearly with time. True.
- Statement 2: The relative acceleration is zero, while the relative velocity is non-zero. True.
- Therefore, both statements are true, and Statement 2 correctly explains Statement 1.
Final Answer
Both statements are true, and Statement 2 is the correct explanation for Statement 1.
---
We have two balls dropped from a tall tower, one after the other. We need to analyze the distance between the two balls after the second ball is dropped and before the first ball hits the ground.
- Let the first ball be dropped at time t=0.
- The second ball is dropped at time t=t0 (let's say after a short interval).
- The first ball will have fallen a distance h1=12gt2 after time t.
- The second ball, dropped at t0, will fall a distance h2=12g(t−t0)2 after the same time t.
The distance y between the two balls at time t after the second ball is dropped can be expressed as:
y=h1−h2
Substituting the expressions for h1 and h2:
y=12gt2−12g(t−t0)2
Expanding (t−t0)2:
y=12gt2−12g(t2−2tt0+t20)
Simplifying:
y=12g(2tt0−t20)
This shows that the distance y depends linearly on time t (since t is the variable).
- The acceleration of both balls is g (downward).
- The relative acceleration between the two balls is:
arel=a1−a2=g−g=0
- The relative velocity between the two balls can be calculated as:
vrel=v1−v2
Since both balls are accelerating downward, the relative velocity is non-zero.
- Statement 1: The distance between the two balls increases linearly with time. True.
- Statement 2: The relative acceleration is zero, while the relative velocity is non-zero. True.
- Therefore, both statements are true, and Statement 2 correctly explains Statement 1.
Both statements are true, and Statement 2 is the correct explanation for Statement 1.
Topper's Solved these Questions
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#1
3 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#2
5 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-03
6 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
Two balls are dropped simultaneously from two points separated by a vertical height of 6 m. The distance of separation between them after next 2s is
View SolutionA ball is dropped downwards . After 1 second another ball is dropped downwards from the same point . What is the distance between them after 3 seconds .
View Solution
Knowledge Check
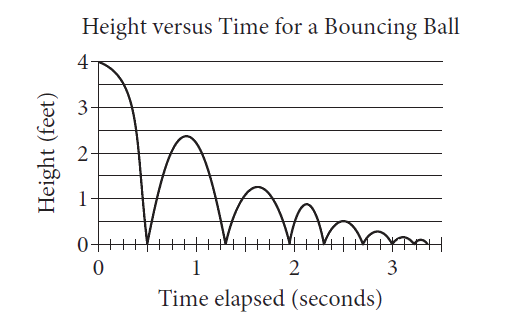
As part of an experiment, a ball was dropped and allowed to bounce repeatedly off the ground until it came to rest. The graph above represents the relationship between the time elapsed after the ball was dropped and the height of the ball above the ground. After it was dropped, how many times was the ball at a height of 2 feet?A1B2C3D4
STATEMENT-1 : Two bodies of mass M and 2M released from rest and they move towards each other due to their mutual gravitational force of attraction and collide at mid point.
STATEMENT-2 : If the total mechanical energy of a body is zero than its linear momentum is necessarily non zero at any point other than reference point.
STATEMENT-3 : The linear momentum of the bob of a simple pendulum suspended by the roof of a car accelerating on a horizontal road increases due to tension in the string of the pendulum.
View SolutionTwo balls are dropped to the ground from different heights. One ball is dropped 2s after the other, but both strike the ground at the same time 5s after the Ist is dropped.
(a) What is the difference in the heights from which they were dropped ?
(b) From what height was the first ball dropped?
View SolutionA body is thrown up with a velocity 40ms−1. At same time another body is dropped from a height 40 m. Their relative acceleration after 1.3 seconds is
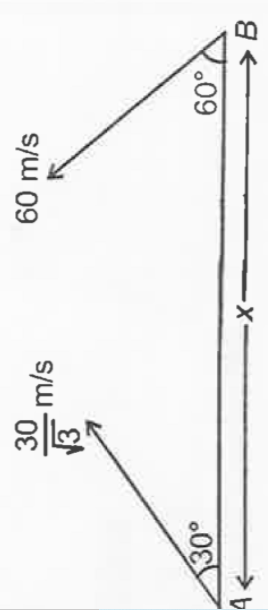
View SolutionTwo balls are projected from two points A and B,x metre apart as shown in figure.The time after which the horizontal distance between them become zero is
View SolutionA ball is dropped from the top of a tower. After 2 s another ball is thrown vertically downwards with a speed of 40ms−1. After how much time and at what distance below the top of tower the balls meet ?
View SolutionA ball is drpped from rest at height 4h. After it has fallen a distance d, a second ball is dropped from rest at height h. What should d be (in terms of h) so that the balls hit the ground at the same time?
View SolutionTwo balls of same mass are dropped from the same height h, on to the floor. The first ball bounces to a height h/4, after the collision & the second ball to a height h/16. The impulse applied by the first & second ball on the floor are I1 and I2 respectively. Then :-
View Solution
