Two balls are dropped simultaneously from two points separated by a vertical height of 6 m. The distance of separation between them after next 2s is
9.8 m
6 m
12 m
0
The correct Answer is:B
To solve the problem, we need to analyze the motion of the two balls dropped from different heights. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Problem
We have two balls dropped from two different heights, separated by a vertical distance of 6 meters. We need to find the distance of separation between them after 2 seconds.
Step 2: Identify Initial Conditions
Both balls are dropped simultaneously, which means:
- Initial velocity of both balls (u₁ and u₂) = 0 m/s (since they are dropped)
- The acceleration due to gravity (g) = 9.81 m/s² (approximately 10 m/s² for simplicity)
Step 3: Calculate the Distance Fallen by Each Ball
Using the equation of motion for distance fallen under gravity:
s=ut+12gt2
Since both balls are dropped from rest (u = 0), the equation simplifies to:
s=12gt2
Step 4: Calculate Distance Fallen After 2 Seconds
Substituting g = 10 m/s² and t = 2 s into the equation:
s=12×10×(2)2
s=12×10×4
s=20 meters
Step 5: Analyze the Separation After 2 Seconds
Since both balls are dropped from rest and have the same acceleration due to gravity, they will fall the same distance in the same time. Therefore, the distance fallen by both balls after 2 seconds is the same.
Step 6: Determine the New Distance of Separation
Initially, the distance of separation between the two balls was 6 meters. After 2 seconds, since both balls have fallen the same distance, the separation remains unchanged.
Thus, the distance of separation after 2 seconds is still:
Distance of separation=6 meters
Final Answer
The distance of separation between the two balls after the next 2 seconds is 6 meters.
---
We have two balls dropped from two different heights, separated by a vertical distance of 6 meters. We need to find the distance of separation between them after 2 seconds.
Both balls are dropped simultaneously, which means:
- Initial velocity of both balls (u₁ and u₂) = 0 m/s (since they are dropped)
- The acceleration due to gravity (g) = 9.81 m/s² (approximately 10 m/s² for simplicity)
Using the equation of motion for distance fallen under gravity:
s=ut+12gt2
Since both balls are dropped from rest (u = 0), the equation simplifies to:
s=12gt2
Substituting g = 10 m/s² and t = 2 s into the equation:
s=12×10×(2)2
s=12×10×4
s=20 meters
Since both balls are dropped from rest and have the same acceleration due to gravity, they will fall the same distance in the same time. Therefore, the distance fallen by both balls after 2 seconds is the same.
Initially, the distance of separation between the two balls was 6 meters. After 2 seconds, since both balls have fallen the same distance, the separation remains unchanged.
Distance of separation=6 meters
The distance of separation between the two balls after the next 2 seconds is 6 meters.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:problems
Explore 47 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:Numerical exercise(LEVEL-1)
Explore 22 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:EXERCISE -II
Explore 80 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 7 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 49 Videos
Similar Questions
Two particles are projected simultaneously from two points O and O' such that 10m is the horizontal and 5m is the vertical distance between them as shown in the figure. They are projected at the same inclination 60∘ to the horizontal with the same velocit 10ms−1. The time after which their separation becomes minimum is
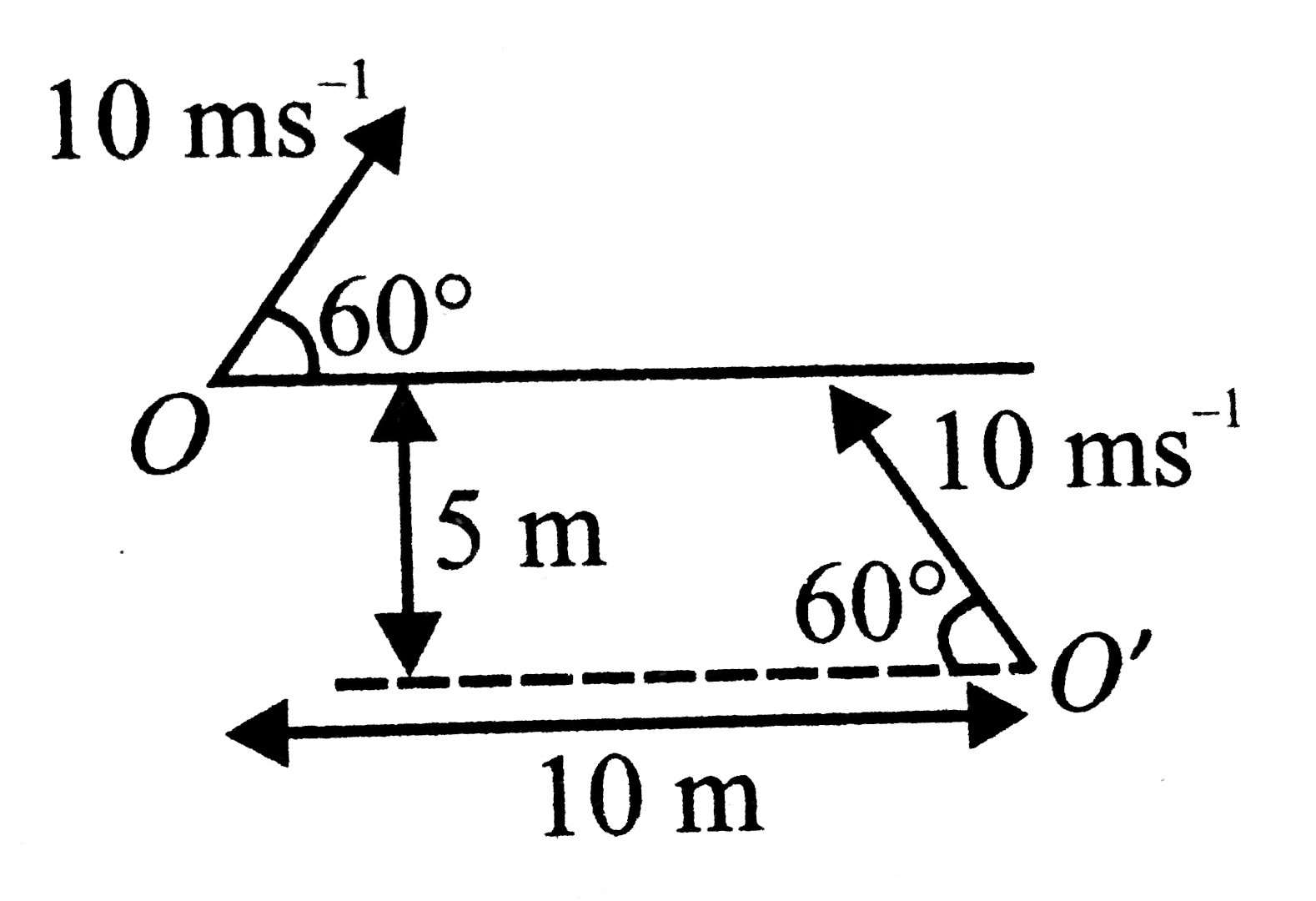
View SolutionTwo particles are projected simultaneously from two points O and O' such that d is the horizontal distance and h is the vertical distance between them as show in figure. These are projected at same inclination α with the horizontal with the same speed v. Find an expression for time at which their separation becomes minimum.

View SolutionA stone is dropped freely, while another thrown vertically downward with an initial velocity of 2ms−1 from the same point, simultaneously. The time required by them to have a distance of separation 22 m between them is
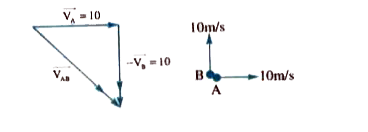
View SolutionTwo particles A and B are projected in air .A is thrown horizontally .B is thrown vertically up . What is the separation between them after 1 sec .
View SolutionA body is dropped from a balloon meving up wigh a velocity of 4ms−2 when the balloon is at a height of 12.5 m from the ground.
The distance of separation between of separation between the body and the balloon after 5 is.
View SolutionSTATEMENT-1: Two balls are dropped one after the other form a tall tower. The distance between them increases linearly with time (elapsed after the second ball is dropped and before the first hits ground).
STATEMENT-2: Relative acceleration is zero, whereas relative velocity non-zero in the above situation.
View SolutionTwo bodies of different masses are dropped simultaneously from same height. If air friction acting on them is directly proportional to the square of their mass, then,
View SolutionA stone is dropped freely while another thrown vertically downward with an initial velocity of 4 m/s from the same point simultaneously. The distance of separation between them will become 30 m after a time of
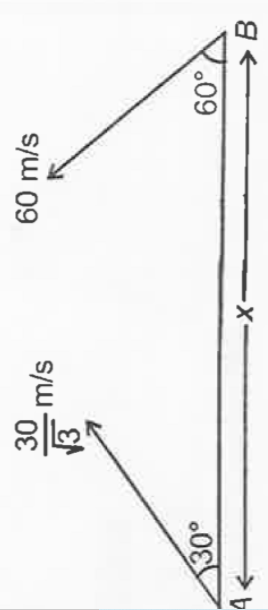
View SolutionTwo balls are projected from two points A and B,x metre apart as shown in figure.The time after which the horizontal distance between them become zero is
View SolutionTwo balls are projected simultaneously with the same speed from the top of a tower-one upwards and the other downwards.If they reach the ground in 6s and 2s ,the height of the tower is
View Solution