A ring rotates about z axis as shown in figure. The plane of rotation is xy. At a certain instant the acceleration of a particle P (shown in figure) on the ring is (6ˆi–8ˆj) m/s2. Find the angular acceleration of the ring & the angular velocity at that instant. Radius of the ring is 2m.

The correct Answer is:−3ˆkrad/s2,−2ˆkrad/s
→a1=6ˆi=→α×→R=→α×2ˆj⇒→α=−3ˆkrad/s2
→ar=−8ˆj=→ω×→v=→ω×(ωR)ˆi⇒→ω=−2ˆkrad/s
Topper's Solved these Questions
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Exercise-04[B]
14 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Exercise-05 [A]
11 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#7
3 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A ring rotates about z axis as shown in figure. The plane of rotation is xy. At a certain instant the acceleration of a particle P (shown in figure) on the ring is (6ˆi−8ˆj)m/s2. Find the angular acceleration of the ring & the abgular velocity at that instant. Radius of the ring is 2m.

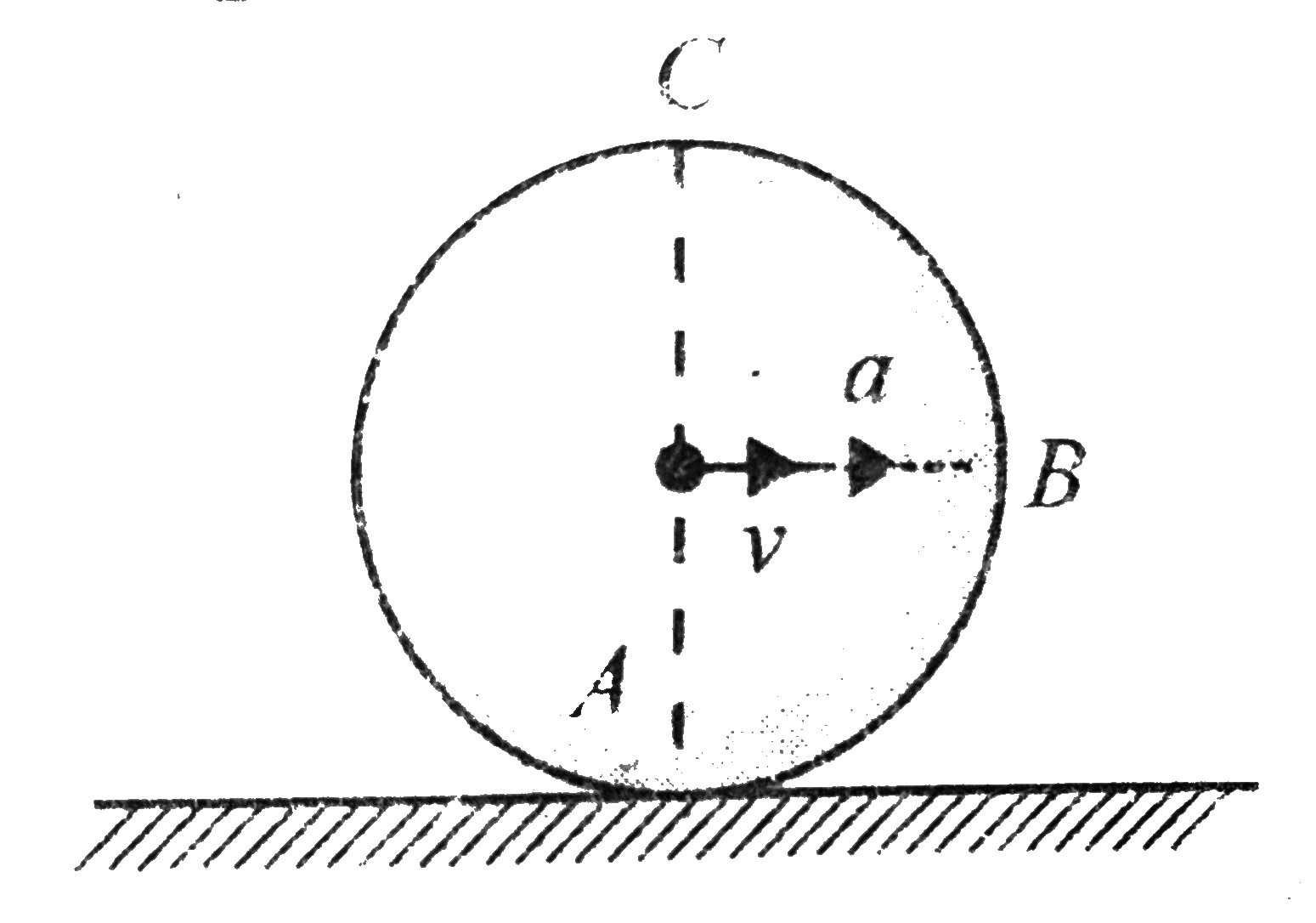
View SolutionA wheel is rolling on a horizontal plane. At a certain instant it has a velocity v and acceleration a of CM as shown in figure . Acceleration of
View SolutionA ring of radius R is rotating about axis of ring such that angular velocity is given as = 5t. Find acceleration of a point P on rim after 5 sec
View Solution
A ring of radius R rolls on a horizontal surface with constant acceleration a of the centre of mass as shown in figure. If ω is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound is
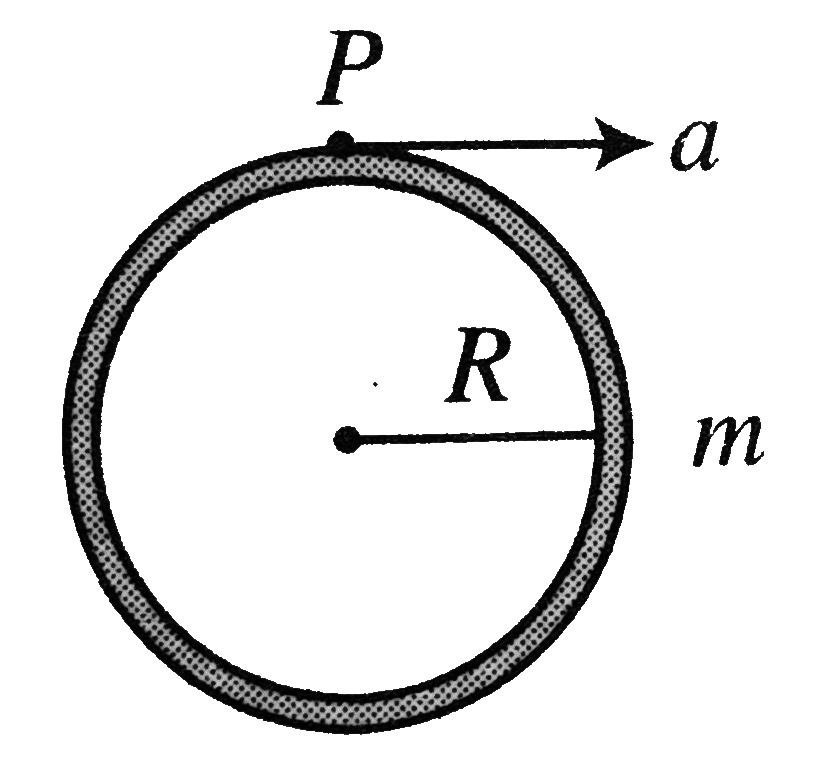
View SolutionA smooth ring of mass m and radius R=1m is pulled at P with a constant acceleration a=4ms−2 on a horizontal surface such that the plane of the ring lies on the surface. Find the angular acceleration of the ring at the given position. (in rad/s2)
View SolutionVelocity of a particle at some instant is v=(3ˆi+4ˆj+5ˆk)m/s. Find speed of the particle at this instant.
View SolutionA constant force F is applied at the top of a ring as shown in figure. Mass of the ring is M and radius is R. Angular momentum of particle about point of contact at time t

View SolutionCalculate the magnitude of linear acceleration of a particle moving in a circle of radius 0.5 m at the instant when its angular velocity is 2.5 rad s–1 and its angular acceleration is 6rads−2.
View SolutionCalculate the magnitude of linear acceleration of a particle moving in a circle of radius 0.5 m at the instant when its angular velocity is 2.5 rad s–1 and its angular acceleration is 6rads−2.
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View Solution
