Two objects of equal mass rest on the opposite pans of an arm balance. Does the scale remain balance when it is accelerated up or down in a life ?
To solve the problem of whether the scale remains balanced when it is accelerated up or down in a lift, we can analyze the forces acting on the two objects on the arm balance.
1. Understanding the Arm Balance:
- An arm balance consists of two pans (or plates) that are suspended from a central pivot. When equal masses are placed on both sides, the balance is in equilibrium.
2. Identifying the Forces:
- Each mass (let's denote them as m) experiences two forces:
- The gravitational force acting downwards, which is mg (where g is the acceleration due to gravity).
- When the lift accelerates, a pseudo force also acts on the masses due to the acceleration of the lift.
3. Acceleration Upwards:
- When the lift accelerates upwards with acceleration A:
- The effective force acting on each mass becomes mg+ma (where a is the acceleration of the lift).
- Thus, the total downward force on each side of the balance is mg+ma.
4. Acceleration Downwards:
- When the lift accelerates downwards with acceleration A:
- The effective force acting on each mass becomes mg−ma.
- In this case, the total downward force on each side of the balance is still balanced because the same mass experiences the same downward acceleration.
5. Conclusion:
- In both cases (upward and downward acceleration), the forces acting on both sides of the arm balance remain equal. Therefore, the arm balance will remain balanced regardless of whether the lift is accelerating upwards or downwards.
Final Answer:
The scale remains balanced when it is accelerated up or down in a lift.
---
- An arm balance consists of two pans (or plates) that are suspended from a central pivot. When equal masses are placed on both sides, the balance is in equilibrium.
- Each mass (let's denote them as m) experiences two forces:
- The gravitational force acting downwards, which is mg (where g is the acceleration due to gravity).
- When the lift accelerates, a pseudo force also acts on the masses due to the acceleration of the lift.
- When the lift accelerates upwards with acceleration A:
- The effective force acting on each mass becomes mg+ma (where a is the acceleration of the lift).
- Thus, the total downward force on each side of the balance is mg+ma.
- When the lift accelerates downwards with acceleration A:
- The effective force acting on each mass becomes mg−ma.
- In this case, the total downward force on each side of the balance is still balanced because the same mass experiences the same downward acceleration.
- In both cases (upward and downward acceleration), the forces acting on both sides of the arm balance remain equal. Therefore, the arm balance will remain balanced regardless of whether the lift is accelerating upwards or downwards.
The scale remains balanced when it is accelerated up or down in a lift.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SWOE44videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I52videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
Similar Questions
Assertion :− Two objects of equal mass rest on the opposite pan of an arm balance. Scale will remains balanced, when it is accelerated up or down in a lift.
Reason :− Both masses experience equal fictitious forces magnitude as well as direction.View SolutionIn the figure a truck is moving on a horizontal surface with acceleration a. Two blocks of equal masses m are supported on the truck as shown in figure. Given that when the block at the top surface is just about to slide, other block remains hanging at 30∘ from the vertical. In this system.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The spring balance A read 2 kg with a block m suspended from it. A balance B reads 5 kg when a beaker with liquid is put on the pan of the balance. The two balances are now so arranged that the hanging is inside the liquid in the beaker as shown in Fig. 15.5.3. In this situation
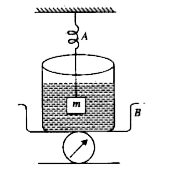 Athe balance A will read more than 2 kgBthe balance B will read more than 5 kgCthe balance A will read less than 2 kg and B will more than 5 kgDthe balance A and B will read 2 kg and 5 kg respectively.
Athe balance A will read more than 2 kgBthe balance B will read more than 5 kgCthe balance A will read less than 2 kg and B will more than 5 kgDthe balance A and B will read 2 kg and 5 kg respectively.
Two identical blocks of mass m are suspended from a beam balance whose scale pans differ in vertical height by h(h<<R), if R and ρ are the radius and density of the earth, then the error in weighing is
 View Solution
View SolutionThe two arms of a balanced are of unequal length. An object when placed in the left pan of the balance weighs 4 kg. The same object when placed in the right pan of the balance weighs 9 kg. The actual (or) true mass of the object is
View SolutionTwo equal masses each in are hung from a balance whose scale pans differ in vertical height by h. The error in weighing in terms of density of the earth ρ is
View SolutionTwo equal masses each in are hung from a balance whose scale pans differ in vertical height by h. The error in weighing in terms of density of the earth ρ is
View SolutionA body of mass 50 kg is hung by a spring balance in a lift. Calculate the reading of the balance when :
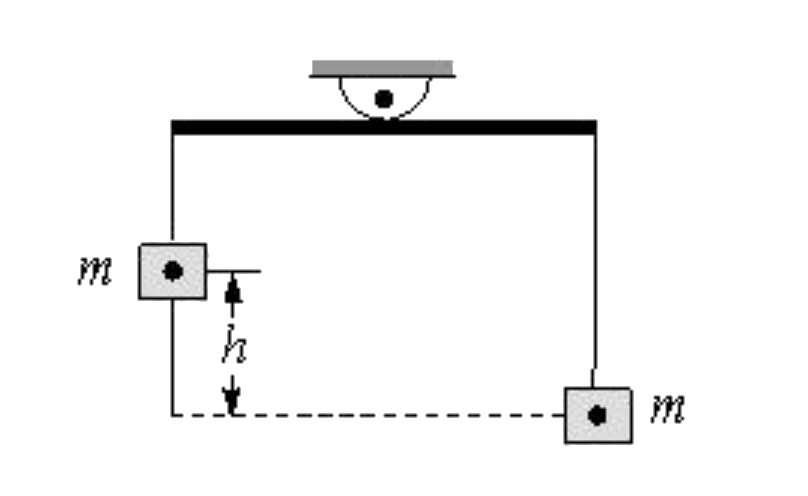
The lift is ascending with an acceleration of 2m/s2.View SolutionTwo blocks of masses m each are hung from a balances as shown in the figure. The scale pan A is at height H1 whereas scale pan B is at height H2 Net torque of weights acting on the system about point C will be (length of the rod is l and H1 & H2 are lt ltR ) (H1>H2)
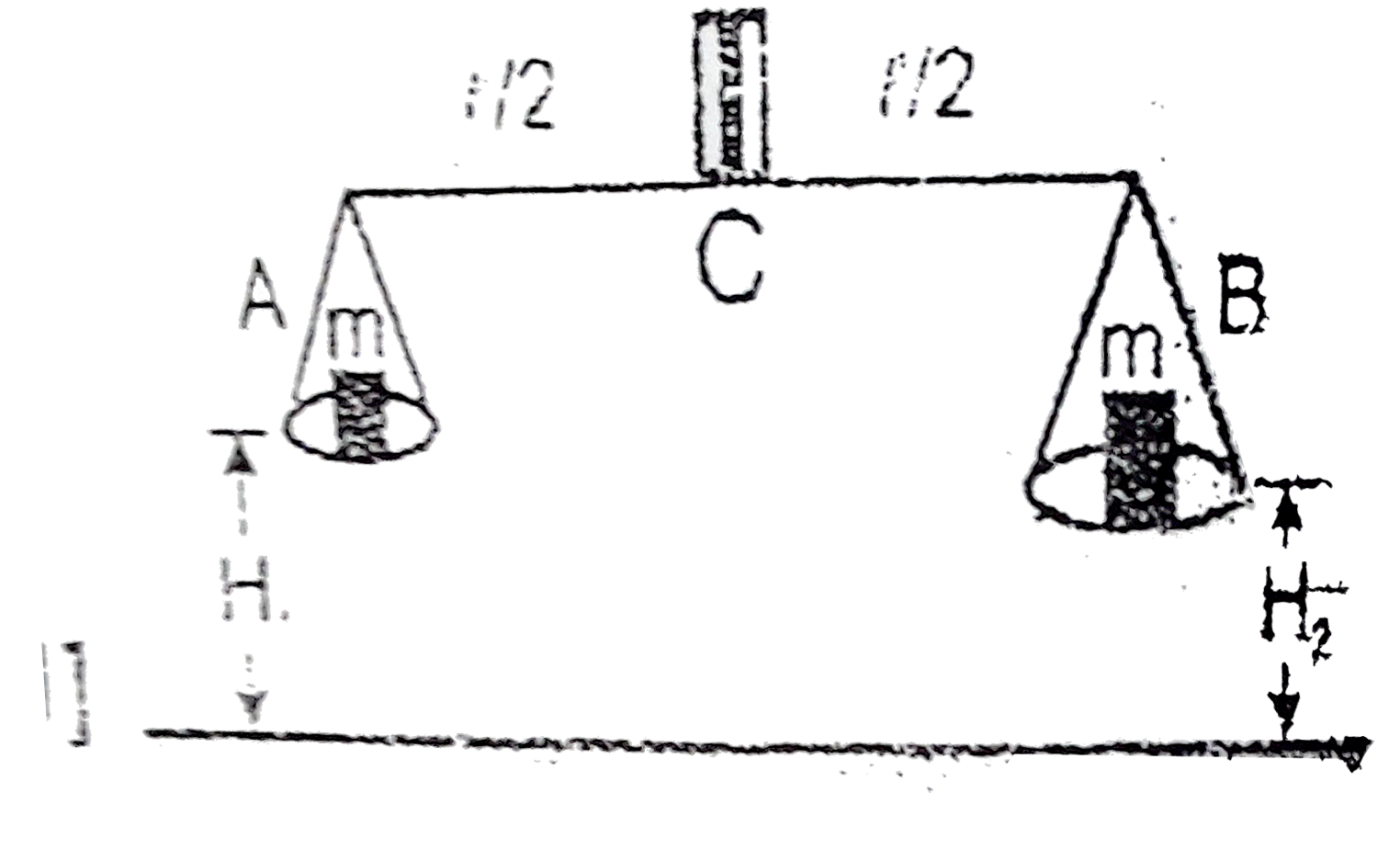 .View Solution
.View SolutionThe spring balance A reads 2 kg with a block m suspended from it. A balance B reads 5kg when a beaker with liquid is put on the pan of the balance. The two balances are now so arranged that the hanging mass in inside the liquid in the beaker as shown in the figure. In this situation:
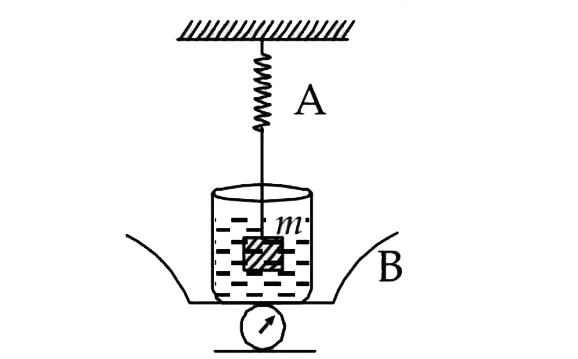 View Solution
View Solution

