Question

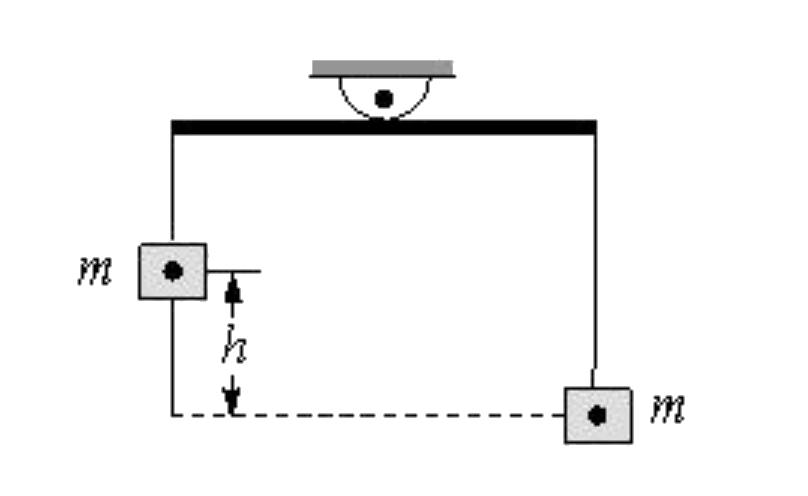
Two equal masses each in are hung from a balance whose scale pans differ in vertical height by $h$. The error in weighing in terms of density of the earth $\rho$ is

Options

A. `πGρmh
`
B. `1/3Gρmh`
C. `8/3πGρmh`
D. `4/3πGρmh
`

Explanation

To solve the problem, we need to find the error in weighing two equal masses when they are hung from a balance with a height difference $$h$$ between the scale pans. Here’s a step-by-step solution:

Step 1: Understand the Weights
Let the mass of each object be \( m \). The weight of the first mass at the surface of the Earth is given by:
\( W_1 = mg \)
where \( g \) is the acceleration due to gravity at the surface.

Step 2: Weight at Height \( h \)
For the second mass that is at a height \( h \), the weight \( W_2 \) can be expressed using the formula for gravitational acceleration at height \( h \):
\( g_h = g \left(1 - \frac{2h}{r}\right) \)
where \( r \) is the radius of the Earth. Therefore, the weight at height \( h \) is:
\( W_2 = mg_h = m \cdot g \left(1 - \frac{2h}{r}\right) \)

Step 3: Calculate the Difference in Weights
The difference in the readings of the balance (error in weighing) is given by:
\( \Delta W = W_1 - W_2 \)
Substituting the expressions for \( W_1 \) and \( W_2 \):
\( \Delta W = mg - m \cdot g \left(1 - \frac{2h}{r}\right) \)
\( \Delta W = mg - mg + \frac{2mgh}{r} \)
\( \Delta W = \frac{2mgh}{r} \)

Step 4: Express \( g \) in Terms of Density
We know that the acceleration due to gravity \( g \) can also be expressed in terms of the density of the Earth \( \rho \):
\( g = \frac{GM}{r^2} \)
where \( M \) is the mass of the Earth. The mass of the Earth can be expressed in terms of its density:
\( M = \rho \cdot V = \rho \cdot \frac{4}{3} \pi r^3 \)
Substituting this into the equation for \( g \):
\( g = \frac{G \left(\rho \cdot \frac{4}{3} \pi r^3\right)}{r^2} = \frac{4}{3} G \rho \pi r \)

Step 5: Substitute \( g \) Back into the Error Equation
Now substitute \( g \) back into the expression for \( \Delta W \):
\( \Delta W = \frac{2mh}{r} \cdot \frac{4}{3} G \rho \pi r \)
The \( r \) cancels out:
\( \Delta W = \frac{8}{3} \pi G \rho mh \)

Final Answer
Thus, the error in weighing in terms of the density of the Earth \( \rho \) is:
\( \Delta W = \frac{8}{3} \pi G \rho mh \)